BCS 方程和 Bogoliubov 是处理对关联的经典内容。一半是学习,一半是为了教学,这里我写下了较为完整的推导过程。我欣赏 Bogoliubov 变换,它把 BCS 波函数变为准粒子真空,在此基础上,构造的准粒子激发可以看做是准粒子的自由气体,这很漂亮,虽然是在粒子数不守恒的 BCS 框架下,也还是很漂亮,具有形式的美感。
参考来源:
P. Ring, P. Shuck, 《The nuclear many-body problem》
Lawson, 《Theory of the nuclear shell model》
1. BCS方程
1.1 拟设
假设波函数的形式为
\[\psi = \prod_{ k >0}
( u_k + v_k a^\dagger_{k} a^\dagger_{\bar{k}} ) |0 \rangle,
\]
\(\bar{k}\)表示\(k\)的时间反演态,\(k>0\)表示\(k\)只遍历一半的单粒子轨道。若\(a^\dagger_k=a^\dagger_{j,m}\),则\(a^\dagger_\bar{k}=(-1)^{j-m}a^\dagger_{j,-m}\)(约定未明)。显然这个波函数形式粒子数是不守恒的,但是第三角动量为 \(M=0\)。
如果定义\(S\)对产生算符
\[S_+(k) = a^\dagger_k a^\dagger_{\bar{k}}, ~~~ S_+ = \sum_{k>0} \frac{v_k}{u_k} a^\dagger_k a^\dagger_{\bar{k}} = \sum_{k>0} \frac{v_k}{u_k} S_+(k).
\]
则
\[\psi = ( \prod_{k>0}u_k ) \prod_{k>0} ( 1 + \frac{v_k}{u_k} S_+(k) ) | 0 \rangle = ( \prod_{k>0}u_k ) ( 1 + \sum_k \frac{v_k}{u_k} S_+(k) + \sum_{k > k'} \frac{v_k v_{k'}}{u_k u_{k'}} S_+(k) S_+(k') + \cdots ) |0 \rangle.
\]
1.2 指数形式
另外,
\[e^{S_+} = e^{ \sum_{k>0} \frac{v_k}{u_k} S_+(k) } | 0 \rangle = \prod_k e^{ \frac{v_k}{u_k} S_+(k)} | 0 \rangle = \prod_{ k >0}
( 1 + \frac{v_k}{u_k} a^\dagger_{k} a^\dagger_{\bar{k}} ) |0 \rangle,
\]
所以有
\[\psi = ( \prod_{k>0}u_k ) e^{ S_+ } | 0 \rangle.
\]
1.3 归一化
\(\psi\)的模方为
\[\langle \psi | \psi \rangle = \langle \prod_{ k >0}
( u_k + v_k a^\dagger_{k} a^\dagger_{\bar{k}} ) | \prod_{ k' >0}
( u_{k'} + v_{k'} a^\dagger_{k'} a^\dagger_{\bar{k'}} ) \rangle
= \prod_k (u^2_k + v^2_k).
\]
我不知道怎么显白地展示上式如何得到,虽然我心里觉得很显然。我想的话,至少可以用归纳法证明,在脑子里想了一下归纳法,确实是的。
所以,如果设定
\[u^2_k + v^2_k = 1,
\]
就可以保证波函数的归一性。
1.4 粒子数期望值
定义
\[\hat{N}_k = a^\dagger_k a_k, ~~~ \hat{N} = \sum_k \hat{N}_k.
\]
而
\[\langle \psi |\hat{N}_k | \psi \rangle = \langle \prod_{ k >0}
( u_k + v_k a^\dagger_{k} a^\dagger_{\bar{k}} )| \hat{N}_k + \hat{N}_{\bar{k}} | \prod_{ k' >0}
( u_{k'} + v_{k'} a^\dagger_{k'} a^\dagger_{\bar{k'}} ) \rangle
= 2 v^2_k,
\]
所以有
\[\langle \psi | \hat{N} | \psi \rangle = 2 \sum_k v^2_k.
\]
1.5 哈密顿量期望值
单体 + 两体的哈密顿量一般形式为
\[\hat{H} = \sum_{k_1, k_2 } t_{k_1 k_2} a^\dagger_{k_1} a_{k_2} + \frac{1}{4} \sum_{ k_1 k_2 k_3 k_4 } V_{k_1 k_2 k_3 k_4} a^\dagger_{k_1} a^\dagger_{k_2} a_{k_4} a_{k_3}.
\]
为了方便计算,可以稍微改写如下,
\[\hat{H} = \sum_{k_1, k_2 } t_{k_1 k_2} a^\dagger_{k_1} a_{k_2} + \sum_{ k_1 > k_2, k_3 > k_4 } V_{k_1 k_2 k_3 k_4} a^\dagger_{k_1} a^\dagger_{k_2} a_{k_4} a_{k_3}.
\]
首先单体算符在BCS波函数上的期望值很容易求:
\[E_1 = \sum_k t_{kk} v^2_k.
\]
然后讨论这种情况:如果\(k_1, k_2\)配对,即\(k_2 = \bar{k}_1\),则\(k_4=\bar{k}_3\),否则期望值为0,得到
\[E^{1}_2 = \sum_{k,k' >0} V_{k \bar{k} k' \bar{k'}} u_k v_k u_{k'} v_{k'},
\]
如果\(k_1, k_2\)不配对,即\(k_2 \neq \bar{k_1}\),则\(k_4 \neq \bar{k_3}\),有
\[E^2_2 = \frac{1}{2} \sum_{k' \neq \bar{k}} V_{k k' k k'} v^2_k v^2_{k'}.
\]
所以,整个哈密顿量的期望值为
\[\langle BCS | \hat{H} | BCS \rangle = \sum_k t_{kk } v^2_k + \sum_{k,k' >0} V_{k \bar{k} k' \bar{k'}} u_k v_k u_{k'} v_{k'} + \frac{1}{2} \sum_{k' \neq \bar{k}} V_{k k' k k'} v^2_k v^2_{k'}.
\]
1.6 BCS方程
标记 \(v_{\bar{k}} = - v_{k}, u_{\bar{k}} = u_k, k>0\),则有
\[\frac{ \partial }{ \partial v_k } \langle BCS | \hat{H} | BCS \rangle = (\frac{\partial}{\partial v_k} + \frac{\partial u_k}{\partial v_k} \frac{ \partial }{ \partial u_k } ) \langle BCS | \hat{H} | BCS \rangle \\
= \sum_k 2(t_{kk} + t_{\bar{k}\bar{k}})v_k + 2 \sum_{k'>0} V_{k \bar{k} k' \bar{k'}} u_k u_{k'} v_{k'} + 2 \sum_{k' \neq \bar{k}} V_{kk'kk'}v_k v^2_{k'} - 2 \sum_{k'>0} V_{k \bar{k} k' \bar{k'}} v^2_k u_{k'} v_{k'} / u_k.
\]
此外,为了保证粒子数期望值为目标值\(N\),还需要添加拉格朗日乘子,再令偏导数为零:
\[\frac{ \partial }{ \partial v_k } \langle BCS | \hat{H} - \lambda \hat{N} | BCS \rangle = 0.
\]
得到的方程为
\[2 \bar{\epsilon_k} u_k v_k + \Delta_k (v^2_k - u^2_k) = 0, k >0.
\]
其中
\[\bar{\epsilon_k} = \frac{1}{2} [ t_{kk} + t_{\bar{k}\bar{k}} + \sum_{k'\neq \bar{k}} (V_{kk'kk'} + V_{\bar{k} k' \bar{k} k'}) v^2_{k'} ] - \lambda,\\
\Delta_k = - \sum_{k'>0} V_{k \bar{k} k' \bar{k'}} u_{k'} v_k.
\]
这里我推的和 Ring&Shuck 书上的结果有点不同,Ring&Shuck 的 \(\bar{\epsilon_k}\) 的定义式右侧求和符号是对所有 \(k'\),我的是对所有 \(k' \neq \bar{k}\)。
如果已知 \(\bar{\epsilon_k}\) 和 \(\Delta_k\),则有
\[v^2_k = \frac{1}{2} [ 1 \pm \frac{ \bar{\epsilon_k} }{ \sqrt{\bar{\epsilon_k}^2 + \Delta^2_k} } ],\\
v^2_k = \frac{1}{2} [ 1 \mp \frac{ \bar{\epsilon_k} }{ \sqrt{\bar{\epsilon_k}^2 + \Delta^2_k} } ].
\]
为了使得 \(\bar{\epsilon_k}<0\) 的轨道占据率高于 \(\bar{\epsilon_k}>0\)的轨道,取
\[v^2_k = \frac{1}{2} [ 1 - \frac{ \bar{\epsilon_k} }{ \sqrt{\bar{\epsilon_k}^2 + \Delta^2_k} } ],\\
v^2_k = \frac{1}{2} [ 1 + \frac{ \bar{\epsilon_k} }{ \sqrt{\bar{\epsilon_k}^2 + \Delta^2_k} } ].
\]
另外还有约束
\[\langle BCS | \hat{N} | BCS \rangle = 2 \sum_{k>0} v^2_k = N,
\]
一共构成 \(\Omega_j +1\) 个非线性方程,通过迭代求解。
1.7 小结
- BCS波函数是一个粒子数不守恒的波函数,可以看作是一个“广义”的波函数,含有粒子数为\(0,2,4,\cdots\)的组态。
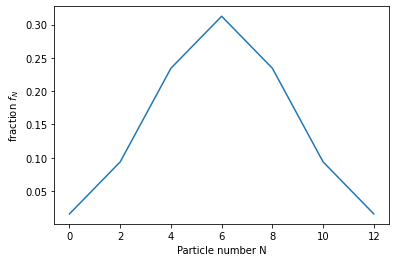
- 因为简单的假设,不同粒子数的组态之间不是自由的,幅度与结构都受假设的限制。如果假设所有\(v_k = v_j, u_k = u_j\),则\(N\)个粒子的组态的几率为\((u_j)^{2\Omega_j}( \frac{v_j}{u_j} )^{N} C^{N/2}_{\Omega_j}\),所以可能是增大再减小。假设 \(\Omega_j = 6, u_j = v_j = \frac{1}{\sqrt{2}}\),则不同粒子数组态的概率为
![image]()
- 如果不是实实在在的粒子,而是激发的类似于声子的准粒子,可能更自然一点。
- 后续的能量最低的要求,是这样一个广义的波函数的能量最低,可以看做若干不同的核的基态的叠加形式的近似。
- 可以看到,哈密顿量期望值中只出现了 \(V_{k\bar{k} k' \bar{k'}}, V_{kk'kk'}\),因为波函数形式的限制,其他关联被排除在外了。
2. Bogoliubov 变换
如前所述,约定\(u_{\bar{k}} = u_k, v_{\bar{k}} = - v_k\),定义新的算符
\[\alpha^\dagger_k = u_k a^\dagger_k - v_k a_{\bar{k}}, \\
\alpha_k = u_k a_k - v_k a^\dagger_{\bar{k}},
\]
那么则有费米子反对易规则:
\[\{ \alpha_k, \alpha_{k'} \} = 0, ~~~~ \{ \alpha_k, \alpha^\dagger_{k'} \} = \delta_{kk'}.
\]
另外,请睁大眼睛,看下面的操作:
\[\alpha_{\bar{k}} \alpha_k | 0 \rangle = ( u_k a_\bar{k} + v_k a^\dagger_k )( u_k a_k - v_k a^\dagger_\bar{k} ) | 0 \rangle
= - v_k ( u_k + v_k a^\dagger_k a^\dagger_\bar{k} ) | 0 \rangle
\]
所以,
\[\prod_k \alpha_k | 0 \rangle = \pm (\prod_{k>0} v_k) | BCS \rangle,
\]
正负号取决于等式左边连乘的顺序。
在这个意义上,把 \(\alpha^\dagger_k\) 看做是准粒子,则 BCS 波函数可以看做是准粒子真空。这个准粒子既具有粒子产生算符,也有粒子湮灭算符,在未占据的高能轨道上,\(v_k\)很小所以准粒子接近粒子,在占据率较高的低能轨道上,\(v_k\)很大所以准粒子接近空穴。当然,这个准粒子是粒子数不守恒的,在这整个笔记中,粒子数都是不守恒的。
![image]()



 浙公网安备 33010602011771号
浙公网安备 33010602011771号