gnuplot 绘制球谐函数图

因为对形变感兴趣，最近在看 P. Ring & P. Schuck 的书。在形变很小（\(\beta << 1\)）时，椭球体的表面可以用低阶球谐函数来近似描述。所以，不妨用gnuplot画两个图出来看看，比较直观，也许以后展示的时候也用得着。

1. 球谐函数

使用 Griffiths 的量子力学教材上的相位约定，球谐函数定义为

\[Y^m_l (\theta, \phi) = \epsilon \sqrt{ \frac{ (2l-1)(l-|m|)! }{ 4 \pi ( l+ |m|)! } } e^{im\phi} P^{|m|}_l(cos\theta), \]

\(m \geq 0\) 时，\(\epsilon = (-1)^m\), \(m\leq 0\)　时有\(\epsilon=1\)。Griffiths的书上写的是\(P^m_l(cos\theta)\)，应该是笔误，因为连带勒让德的\(m\)必须是非负整数，所以我更正为\(P^{|m|}_l(cos \theta)\)。Peter Ring 他们的书应该用的相同的相位约定，因为他们提到\(Y^*_{\lambda \mu} = (-1)^\mu Y_{\lambda -\mu}\)，与这个定义一致。

2. gnuplot 绘制三维参数图

我先尝试了python的绘图，从网上抄了一段代码试了试，发现还没有我熟悉的gnuplot好使，所以决定用gnuplot。

2.1 python 绘制三维图

下面是那段python代码

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt, numpy as np
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d' )
u = np.linspace( 0, 2*np.pi, 1000)
v = np.linspace( 0, 2*np.pi, 1000)
x = np.outer( np.cos(u), np.sin(v) )
y = np.outer( np.sin(u), np.sin(v) )
z = np.outer( np.ones(np.size(u)), np.cos(v))
ax.plot_surface( x, y, z, cmap = 'rainbow' )

得到图片：

我有以下抱怨：
①三维图不能旋转视角，这点真远不如 gnuplot
②图片小，不够清楚
③代码细节太多，需要手动地定义所有离散的 x, y, z 坐标

2.2 gnuplot 绘制三维图

下面是我写的 gnuplot 脚本，用来绘制同样的三维球面

set param       # 参数图模式
# set pm3d depthorder   # 前面的色块挡住后面的，形成立体感
set urange [0:pi]       # 设置 u, v 的取值范围
set vrange [0:2*pi]
set iso 30              # 值越大取点越多
set view equal xyz      # 显示时 x, y, z 三个坐标标度一致
unset tics              # 不显示坐标轴
unset border            # 不显示边框
splot sin(u)*cos(v), sin(u)*sin(v), cos(u) 

画出来的球体：

如果想画彩图，打上灯光，弄得美美的，可以如下：

set param       # 参数图模式
set pm3d depthorder     # 前面的色块挡住后面的，形成立体感
set pm3d lighting primary 0.5 specular 0.6
set palette rgbformulae 7, 5, 15
set urange [0:pi]       # 设置 u, v 的取值范围
set vrange [0:2*pi]
set iso 100             # 值越大取点越多
set view equal xyz      # 显示时 x, y, z 三个坐标标度一致
unset tics              # 不显示坐标轴
unset border            # 不显示边框
splot sin(u)*cos(v), sin(u)*sin(v), cos(u) w pm3d

效果如下：

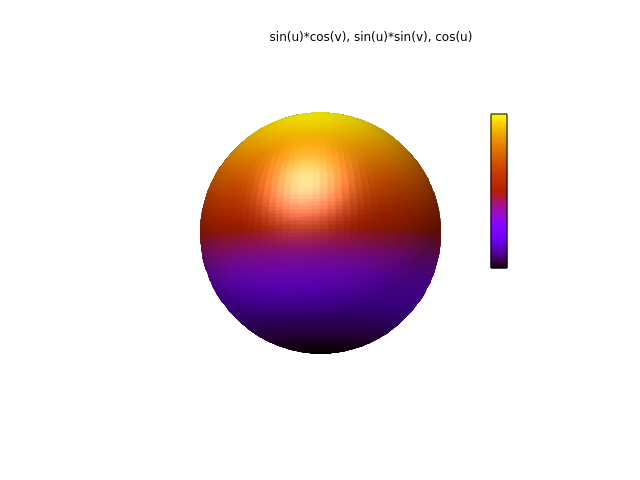
3. gnuplot 绘制低阶球谐函数

我们要对低阶球谐函数，制作 \(R(\theta, \phi) = Y^m_l(\theta, \phi)\) 的图。以下是 Griffiths 的书上的表格。

显然，\(Y^0_0\)就是一个球体。下面挨个画，苦哈哈。注意，为了方便，我略去了所有归一化因子。

3.1 \(Y^m_1\)

gnuplot 脚本如下，不仅做球谐函数的图，也做了一个球形网格，作为相对位置参考。

set param       # 参数图模式
set pm3d depthorder     # 前面的色块挡住后面的，形成立体感
set pm3d lighting primary 0.5 specular 0.6
set palette rgbformulae 7, 5, 15
set urange [0:pi]       # 设置 u, v 的取值范围
set vrange [0:2*pi]
set iso 50              # 值越大取点越多
set view equal xyz      # 显示时 x, y, z 三个坐标标度一致
unset tics              # 不显示坐标轴
unset border            # 不显示边框
set dummy u,v
set multiplot layout 1,2
# subplot
r(u) = cos(u)
splot r(u)*sin(u)*cos(v), r(u)*sin(u)*sin(v), r(u)*cos(u) w pm3d t "R({/Symbol q },{/Symbol j})=Y^0_1 ( {/Symbol q },{/Symbol j} )", sin(u)*cos(v), sin(u)*sin(v), cos(u) t "Sphere for reference"
# subplot
set urange [0:pi]
r(u) = sqrt(0.5)*sin(u)
splot r(u)*sin(u)*cos(v), r(u)*sin(u)*sin(v), r(u)*cos(u) w pm3d t "R({/Symbol q },{/Symbol j})=Y^1_1 ( {/Symbol q },{/Symbol j} )", sin(u)*cos(v), sin(u)*sin(v), cos(u) t "Sphere for reference"
unset multiplot

彩图如下：

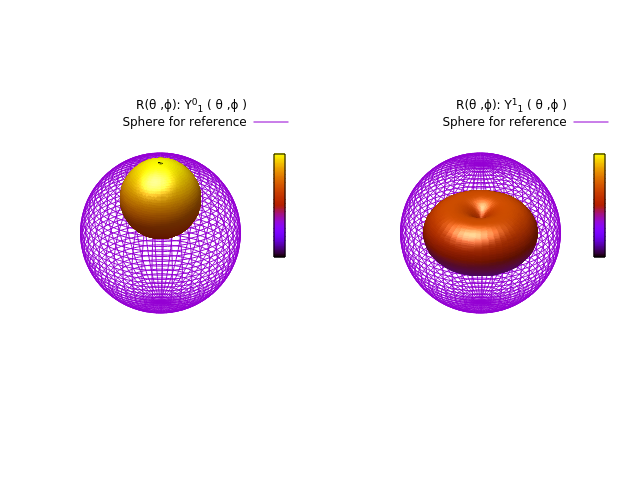
可见，\(Y^0_1\)是个球体，偏离球心一段距离，这可以推导出来，因为\(Y^0_1 \propto cos(\theta) e^{im\phi}\)，所以

\[x = cos(\theta) sin(\theta) cos(\phi) = \frac{1}{2} sin(2\theta) cos(\phi), \\ y = cos(\theta) \cos(\theta) sin(\phi) = \frac{1}{2} \sin(2\theta) \sin(\phi), \\ z = cos(\theta) \cos(\theta) = \frac{1}{2} \cos(2\theta) + \frac{1}{2}. \]

确实表征一个球体(每个点被描绘2次)沿 \(z\) 方向向上偏离。
但是 \(|Y^{\pm 1}_1 |\) 的形状是一个 Donut，为何 Peter Ring 说也表征球体平移，我就不懂了。

3.2 \(Y^{m}_2\)

set param       # 参数图模式
set pm3d depthorder     # 前面的色块挡住后面的，形成立体感
set pm3d lighting primary 0.5 specular 0.6
set palette rgbformulae 7, 5, 15
set urange [0:pi]       # 设置 u, v 的取值范围
set vrange [0:2*pi]
set iso 50              # 值越大取点越多
set view equal xyz      # 显示时 x, y, z 三个坐标标度一致
unset tics              # 不显示坐标轴
unset border            # 不显示边框
set dummy u,v
set multiplot layout 1,3
# subplot
r(u) = 0.5*(3*cos(u)*cos(u)-1)
splot r(u)*sin(u)*cos(v), r(u)*sin(u)*sin(v), r(u)*cos(u) w pm3d t "R({/Symbol q },{/Symbol j}): Y^0_2 ( {/Symbol q },{/Symbol j} )", sin(u)*cos(v), sin(u)*sin(v), cos(u) t "Sphere for reference"
# subplot
r(u) = 0.5*3*sin(u)*cos(u)
splot r(u)*sin(u)*cos(v), r(u)*sin(u)*sin(v), r(u)*cos(u) w pm3d t "R({/Symbol q },{/Symbol j}): Y^1_2 ( {/Symbol q },{/Symbol j} )", sin(u)*cos(v), sin(u)*sin(v), cos(u) t "Sphere for reference"
# subplot
r(u) = 0.25*3*sin(u)*sin(u)
splot r(u)*sin(u)*cos(v), r(u)*sin(u)*sin(v), r(u)*cos(u) w pm3d t "R({/Symbol q },{/Symbol j}): Y^2_2 ( {/Symbol q },{/Symbol j} )", sin(u)*cos(v), sin(u)*sin(v), cos(u) t "Sphere for reference"
unset multiplot

得到图：

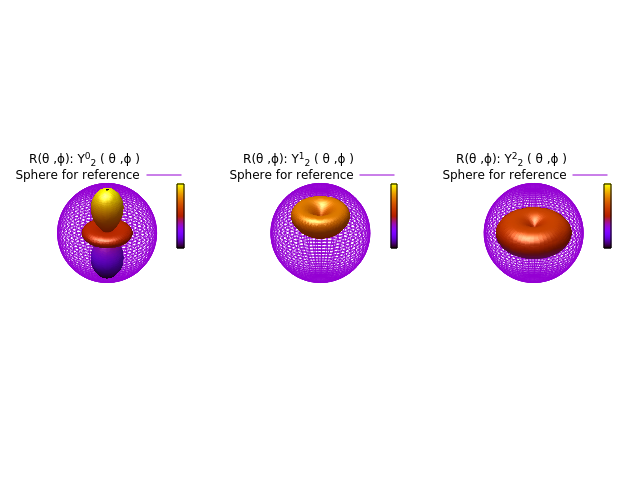
没弄明白怎么和椭球体联系起来。