MPI学习笔记（二）：梯形法数值积分

今天尝试了一个简单的小程序，用 MPI 并行计算定积分。

代码来源自：https://www.cnblogs.com/hantan2008/p/5390375.html#4248681

其中有点小错误，我做了一点修改。然后测试了并行效率，作图记录于此。

代码如下：

#include<iostream>
using namespace std;

#include"mpi.h"
#include<cmath>

double f(double x){
    return pow(x,3);
}

double Trap(double left_endpt, double right_endpt, double trap_count, double base_len){

    double estimate = ( f(left_endpt) + f(right_endpt) )/2, x = left_endpt;

    for(int i=1;i<=trap_count-1;i++){
        x += base_len;
        estimate += f(x);
    }
    estimate = estimate * base_len;
    return estimate;
}

int main(){

    int my_rank = 0, comm_sz = 0, n = 1E7, local_n = 0;
    double a = 0, b = 3, h = 0, local_a = 0, local_b = 0;
    double local_int = 0, total_int = 0;
    int source;
    clock_t t_start = clock();

    MPI_Init( NULL, NULL );
    MPI_Comm_rank( MPI_COMM_WORLD, & my_rank );
    MPI_Comm_size( MPI_COMM_WORLD, & comm_sz );

    double start_time = MPI_Wtime();

    h = (b-a)/n; 
    local_n = n / comm_sz;
    if( my_rank == comm_sz - 1 ){
        local_n = n - local_n * (comm_sz-1);
    }// when n is not indivisible by comm_sz, the last chunk is larger than others.

    local_a = a + my_rank * ( n / comm_sz ) * h;
    local_b = local_a + local_n * h;
    local_int = Trap( local_a, local_b, local_n, h );
    //printf("%d of %d processes, local_int = %.15e\n", my_rank, comm_sz, local_int);

    if( my_rank != 0 ){
        MPI_Send( & local_int, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD );
    }
    else{
        total_int = local_int;
        for( source = 1; source < comm_sz; source ++ ){
            MPI_Recv( & local_int, 1, MPI_DOUBLE, source, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE );
            total_int += local_int;
        }

        printf("With n = %d trapezoids, our estimate \n", n);
        printf("of the integral from %f to %f = %.15e\n", a, b, total_int );

        double end_time = MPI_Wtime();
        printf("That took %lf seconds.\n", end_time - start_time);    
    }

    MPI_Finalize();

    return 0;
}

其中 MPI_Send 和 MPI_Recv 是点对点通信函数，而 MPI_Wtime 读取当前进程当时的时刻，程序中打出的是进程 0 的所用时间，用来标定整个程序的用时。

编译并运行：

mpicxx trapzoid_integral.cpp -o a.out
mpirun -np 2 ./a.out

其中 2 表示征用的核数。于是我在我的 24 core 电脑上试用了一下。计算结果无误，约为 20.25. 下图是总时间与进程数的函数关系。

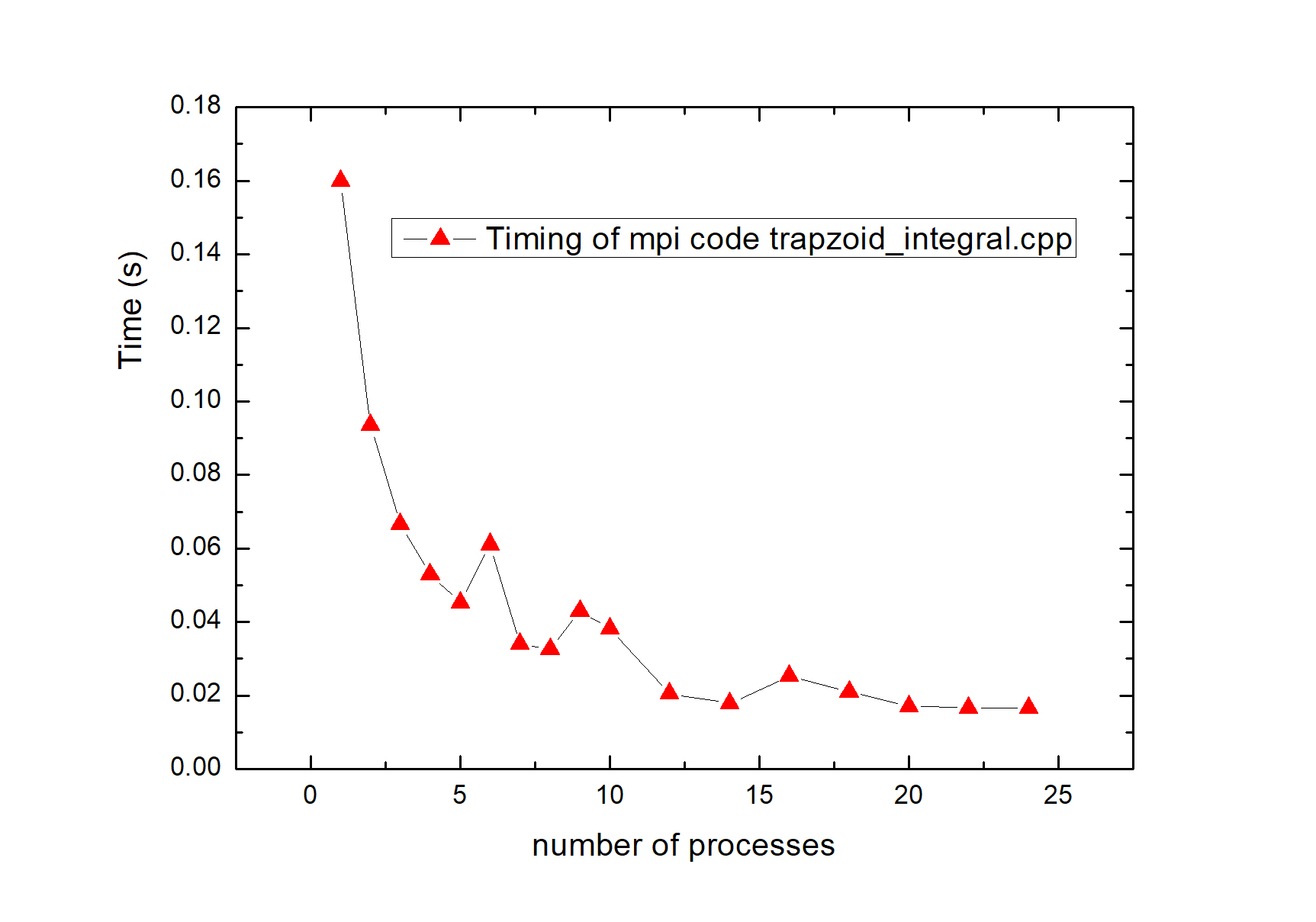
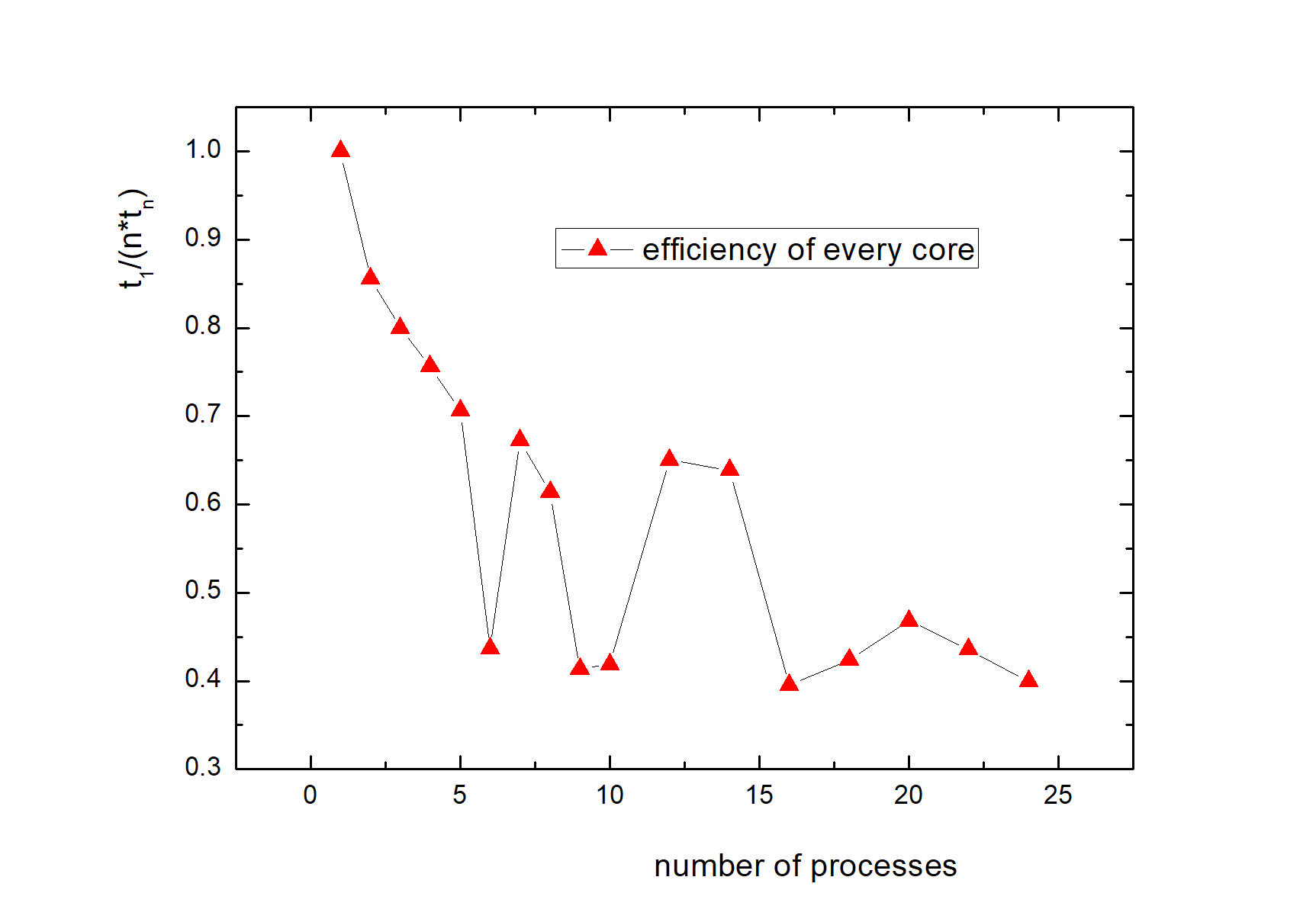
上面第一张图是整个程序耗时，可见进程数加到大约 14 根的时候，整体时间就几乎不下降了。第二张图是每个进程单位时间内完成的工作量，整体是下降的，也就是说，相比 1 根进程，10 根进程不能使总时间变为 1/10。