C++ 尾递归优化
参考来源:https://blog.csdn.net/fall221/article/details/9158703
用 C++ 重现了一遍。
例子:裴波拉契数列: 1,1,2,3,5,8,。。。
用递归求第 n 项:
double fabonacci(int n){//normal recursion
if(n<=0){
cout<<"wrong parameter for fabonacci(n)!"<<endl;
}
else if(n==1){
return 1;
}
else if(n==2){
return 1;
}
else{
return fabonacci(n-1) + fabonacci(n-2);
}
}
上面这个算法的时间复杂度是 O(2^n),比如
fab(6)
= fab(5) + fab(4)
= fab(4) + fab(3) + fab(3) + fab(2)
= fab(3) + fab(2) + fab(2) + fab(1) + fab(2) + fab(1) + fab(2)
= fab(2) + fab(1) + fab(2) + fab(2) + fab(1) + fab(2) + fab(1) + fab(2)
如果不是从 fab(6) 开始,是从 fab(n) 开始,n 又足够大,上式中每行 fab() 个数为 1,2,4,8,16,。。。
所以 fab() 被调用的次数为 O(2^n) 数量级,时间复杂度为 O(2^n)
double tail_fabonacci(int a, int b, int n){
// tail recursion
if(n<0){
cout<<"wrong parameter for tail_fabonacci(int, double *)!"<<endl;
}
else if(n==0) return a;
else if(n==1) return b;
else{
return tail_fabonacci(b, a+b, n-1);
}
}
这个算法已经包括了动态规划的意思,从 fab(0), fab(1) 出发,迭代大约 n 次,即可得到结果,时间复杂度为 O(n),所以算法本身就更优越。
int main(){
int n;
cout<<"n=";
cin>>n;
time_t t_start=time(0);
cout<<"fabonacci(n)="<<fabonacci(n)<<endl;
time_t t_middle=time(0);
cout<<"tail recursion: fabonacci(n)="<<tail_fabonacci(0,1,n)<<endl;
time_t t_end=time(0);
cout<<"time to calculate normal recursion:"<<t_middle - t_start<<"s"<<endl;
cout<<"time to calculate tail recursion:"<<t_end - t_middle<<"s"<<endl;
cout<<"total time:"<<t_end-t_start<<"s"<<endl;
return 0;
}
编译: g++ main.cpp -o main.o
运行结果:
n=50
...
time to calculate normal recursion:186s
time to calculate tail recursion:0s
这很正常。下面是重点——关于尾递归优化。
如果不加 -O2,编译时不会自动做尾递归优化,(我估计)每次递归没有擦去上次的栈帧,所以空间复杂度还是 O(n)。可做实验:注掉调用 fabonacci(n) 那一行,即只测试尾递归,进行编译
g++ main.cpp -o main.o
./main.o
n=1000000
segmentation fault (core dumped)
据我目测,估计是栈内存溢出了。
但如果加上 -O2 进行编译,就可实现尾递归优化
g++ main.cpp -o main.o -O2
./main.o
n=10000000000
tail recursion: fabonacci(n)= -1.07027e+09
time to calculate tail recursion: 3s
上面的结果中,fabonacci(n)= -1.07027e+09 为负值是因为超出了整型范围。但 n=10^{10} 也可以算出来,说明栈内存没有爆。据我目测,耗时 3s 是正常的,因为 10^10 次加法,cpu 3点几的GHz,差不多。
另写了个循环函数
double iter_fabonacci(int a, int b, int n){
for(int i=0;i<n-1;i++){
int temp=a;
a=b;
b=temp+b;
}
return b;
}
然后测试了这个循环函数与尾递归函数(开启尾递归优化,即开启 -O2)的耗时对比,如下图
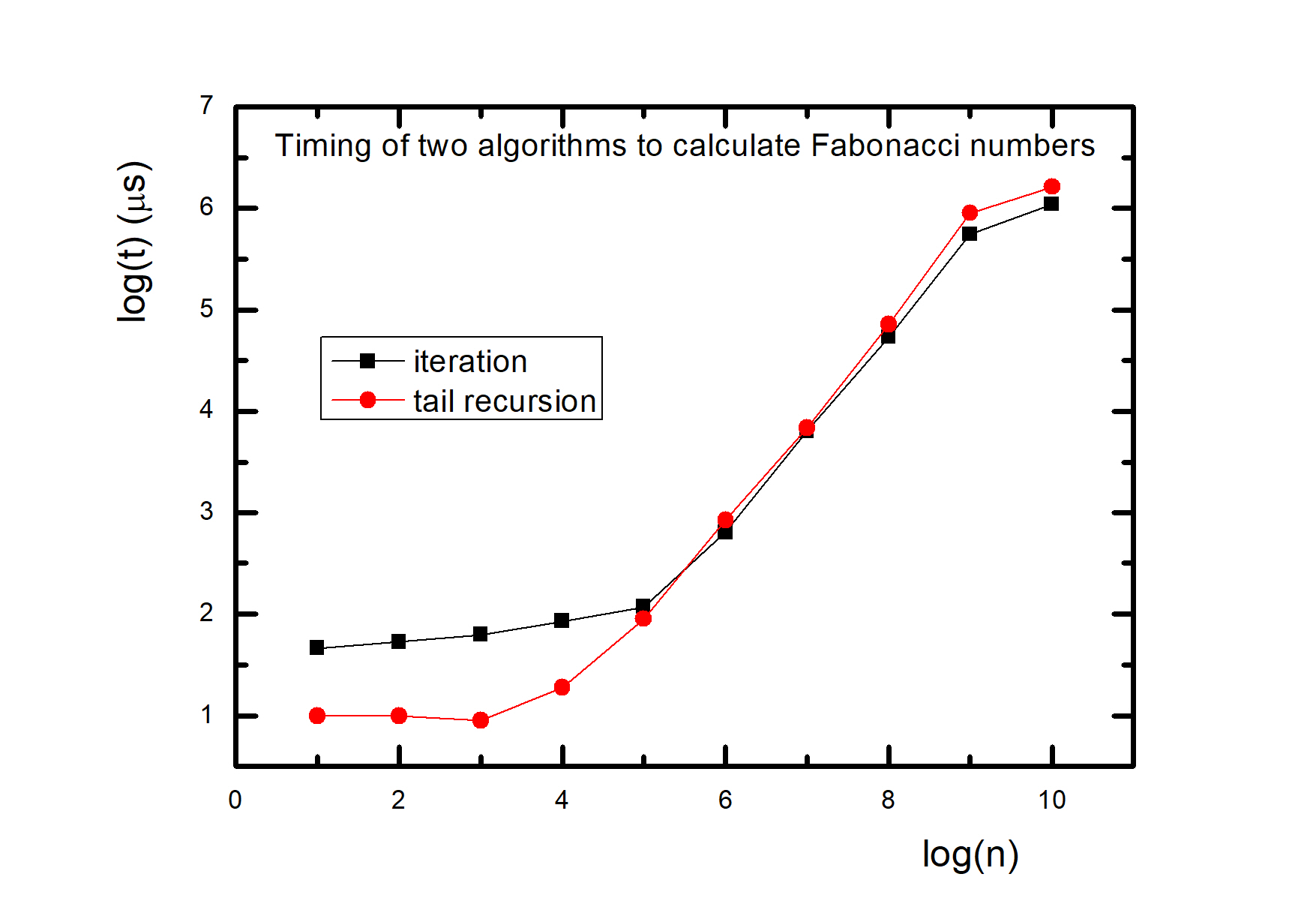
用的是 c++ time.h 里的 clock_t 类型,以及 clock() 函数,比如:
clock_t t_start=clock();
cout<<"\t\t\tfabonacci(n)="<<iter_fabonacci(0,1,n)<<endl;
clock_t t_end=clock();
cout<<"time to do iterations: "<<t_end-t_start<<" microsecond"<<endl;
linux 下 clock() 返回值的单位是 微秒,不信可以加一行
cout<<CLOCKS_PER_SECOND<<endl;
会输出 1000000,即单位是 1/1000000 s = 1 微秒。
-----------------------------------------------------------------------------------------------------------
我发现了一个问题,如果在尾递归函数中加入一行:
double tail_fabonacci(int a, int b, int n){
// tail recursion
cout<<&a<<"\t"<<&b<<endl;
if(n<0){
cout<<"wrong parameter for tail_fabonacci(int, double *)!"<<endl;
}
else if(n==0) return a;
else if(n==1) return b;
else{
return tail_fabonacci(b, a+b, n-1);
}
}
新加入的这一行 cout<<&a<<"\t"<<&b<<endl; 本意是想看看内存地址的变化,看看是不是真的没有栈开销,但加入这一行以后,再用 “-O2” 编译,运行可执行文件,发现 n=1000000 时就报错 “segmentation error”,似乎尾递归优化失效,和没有加 “-O2” 没有区别了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号