字符串匹配算法--KMP
一、KMP算法基本介绍
1、改进的字符串匹配算法
2、由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特-莫里斯-普拉特操作(简称KMP算法)
3、每当一趟匹配过程中出现字符比较不等时,不需要回溯i指针,而是利用已经得到的“部分匹配”的结果将模式串向后“滑动”尽可能远的一段距离后,继续进行比较。这样利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的
4、具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息
5、时间复杂度O(m+n)
二、KMP算法的几个问题
1、问:当主串中第𝑖个字符与模式中第𝑗个字符不相等时,主串中第𝑖个字符( 𝑖指针不回溯)应与模式中哪个字符再比较??
假设:主串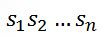 ,模式串
,模式串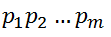 ,此时要与模式串中第k(k<j)个字符继续比较,则模式中前k-1个字符的子串都必须满足下列公式,且不存在k’>k满足以下公式1:
,此时要与模式串中第k(k<j)个字符继续比较,则模式中前k-1个字符的子串都必须满足下列公式,且不存在k’>k满足以下公式1: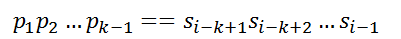 ;
;
虽然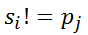 ,但是
,但是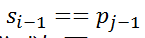 ,且前k-1个都相同,因此可以得到部分匹配的结果,公式2:
,且前k-1个都相同,因此可以得到部分匹配的结果,公式2: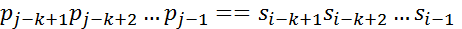
公式1和公式2可以推出公式3: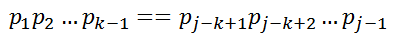 ,其中1<k<j,且不存在k'>k满足公式3
,其中1<k<j,且不存在k'>k满足公式3
综上所述:在当匹配过程中,主串中第i个字符和模式中第j个字符比较不相等时,仅需将模式串向后滑动至模式串中第k个字符和主串中第i个字符再进行比较
答:求出模式串第𝑗个字符与主串第𝑖个字符不等时,模式串中需要重新和主串第𝑖个字符进行比较的字符的位置- 𝑘
2、问:怎么求出模式串第𝑗个字符与主串第𝑖个字符不等时,模式串中需要重新和主串第𝑖个字符进行比较的字符的位置(模式串向右滑动到模式串第几位)- 𝑘??
由上述可得,模式串的next函数定义:
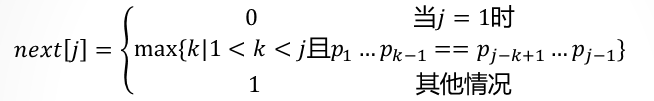
由上述定义可知:next[1]=0
设next[j]=k,则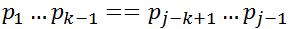
求:next[j+1]=??
情况1:若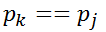 ,则
,则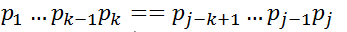 ,推出:
,推出: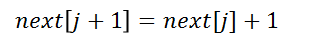
情况2:若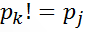 ,则
,则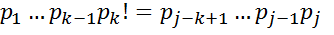 ,next[j+1]=??
,next[j+1]=??
(1)、设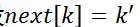 ,则
,则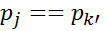 ,推出公式4:
,推出公式4: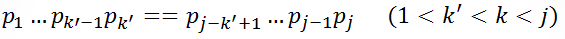
因此: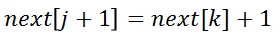
(2)、若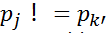 ,则继续第next[k']个字符和pj对齐比较,以此类推,直到pj和某个字符匹配成功
,则继续第next[k']个字符和pj对齐比较,以此类推,直到pj和某个字符匹配成功
(3)、不存在任何k'满足公式4,则next[j+1]=1
3、综上所述,next函数代码如下:
void get_Next_val(std::vector<std::string> vSub, int next[]) { if(next == NULL) { printf("next is null\n"); return ; } int iLen = vSub.size(); int i=0, j=-1;//vSub下标从0开始 next[0] = -1; while(i < iLen-1) { if(j==-1 || strncmp(vSub[i].c_str(), vSub[j].c_str(), vSub[i].length())==0 ) { ++i; ++j; next[i]=j; } else { j = next[j]; } } return; }

三、KMP匹配过程代码
//返回匹配成功的位置,-1表示没有匹配成功,可以再加一个入参,指定从哪一位开始匹配 int KMP(std::vector<std::string> vMainStr, std::vector<std::string> vSubStr) { int i=0, j=0; int iLen1 = vMainStr.size(); int iLen2 = vSubStr.size(); //next[] int* next = new int[iLen2]; for(int i=0; i<iLen2; i++) { next[i] = 0; } get_Next_val(vSubStr, next); #if 1 for(int i=0; i<iLen2; ++i) { printf("vStr[%d]=%s\t", i, vSubStr[i].c_str()); } printf("\n"); for(int i=0; i<iLen2; i++) { printf("next[%d]=%d\t", i, next[i]); } printf("\n"); #endif int iLoop=0; while(i<iLen1 && j<iLen2) { iLoop++; if(j==-1 || vMainStr[i] == vSubStr[j]) { ++i; ++j; } else { j = next[j]; } } //删除next delete []next; if(j>=iLen2)//j到模式串的最后一个下标,最后一个下标+1等于len { return i-iLen2;//返回匹配到的主串位置 } return -1;//-1表示没有找到 }

四、KMP算法的优缺点
1、kmp算法仅当模式串与主串存在许多部分匹配的情况下才显得比朴素匹配算法快得多
2、kmp算法的最大特点是指示主串的指针不需回溯,整个匹配过程,对主串仅需从头到尾扫描一边,这对处理从外设输入的庞大文件很有效,可以边读入边匹配,而不需要回头重读




