Matlab 实现连续PID环节与标记系统-3dB点

Matlab 实现连续PID环节

连续PID环节传递函数：

\[\frac{O(s)}{I(s)} = K_P \cdot \left( 1 + \frac{K_{I}}{s} + K_D\cdot s \right) \]

使用Matlab脚本实现连续PID环节传递函数：先用一个\(K_P\)环节，然后与积分环节 \(K_I / s\) 并联，然后再与微分环节 \(K_D * s\) 并联，即得到了连续PID环节的传递函数。之后再与系统开环传递函数串联，之后再增加负反馈，即可得到闭环控制系统传递函数。具体是实现代码：

clc;
clear;
close all;

Target = 1000;  %目标值
sys1= tf([0,300,200,350],[1,0.5,0.05,0]);   %建立被控对象传递函数 零点为-1  极点为-50
%sys2=tf([0.02 1],1);   %建立被控对象传递函数 无零点  极点为-20

%PID传递函数
Kp = 1;
Ki = 0.1;
Kd = 0;

sysP = Kp;
sysI = tf(Ki,[1,0]);
sysD = tf([Kd,0],1);
sysPI = parallel(sysP,sysI);  %将比例积分微分环节并联得到PID传递函数
sysPID =  parallel(sysPI,sysD);

sysG = series(sysPID,sys1);  %将两传递函数串联 得到最终的传递函数G

sysH = 1;  %反馈函数为空
sysResult = feedback(sysG,sysH);  %负反馈
step(Target * sysResult,0.5);  %串联并加入反馈后的传递函数阶跃

得到曲线如下：

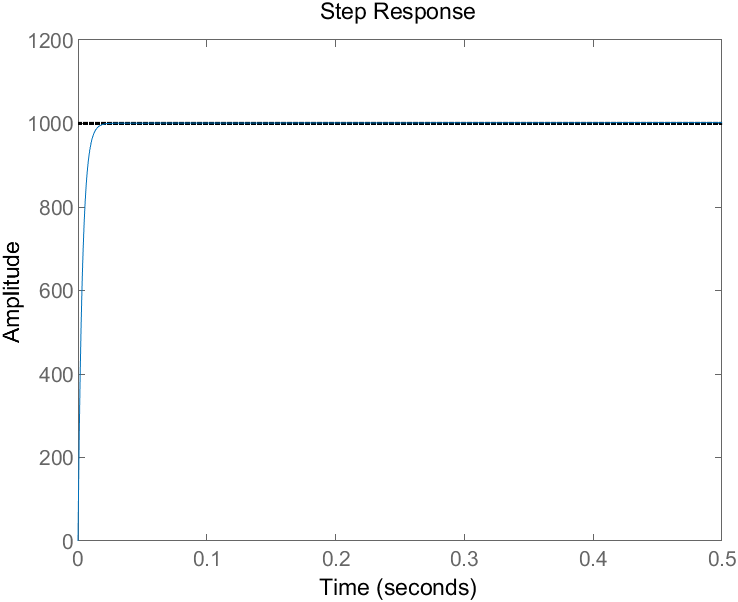
标记-3dB点

% 频段带宽
f_begin = 1e-3;
f_final = 1e3;
f = linspace(f_begin,f_final,1e6)';

% 传递函数
sysHclose = feedback(sysG,sysH);  % 负反馈 闭环传递函数
% 计算幅频和相频响应
h = freqs(cell2mat(sysHclose.num),cell2mat(sysHclose.den),w);
amplitude = abs(h); % 幅频响应
mag = 20*log10(amplitude);
phase = angle(h); % 相频响应
phesedeg = phese*180/pi;
% 绘图
figure;
subplot(2,1,1)
semilogx(f,mag);
grid on; xlim([f_begin f_final]);
subplot(2.1.2)
semilogx(f,phesedeg);
grid on; xlim([f_begin f_final]);

% -----添加谐振点-----
magnitude = mag;
[magmax,fmax] = max(magnitude);    %谐振点为幅频曲线的极值点
fmax = f(fmax);
 
plot(fmax,magmax,'o','LineWidth',2,'MarkerSize',5,'MarkerEdgeColor','k')
text(fmax,magmax-2,sprintf('Resonance point:\n(%.3f Hz, %.3f dB)',fmax,magmax),...
    'VerticalAlignment','top','HorizontalAlignment','right')
%'VerticalAlignment','bottom'
hold on;
 
% -----添加-3dB带宽点-----
B=abs(magnitude+3.0);
[x,index]=sort(B);       %为了得到最接近-3dB的值，先对绝对值进行排序，index为排序前的坐标值
mag_3db=magnitude(index(1));
f_3db=f(index(1));
 
plot(f_3db,mag_3db,'o','LineWidth',2,'MarkerSize',5,'MarkerEdgeColor','r')
text(f_3db,mag_3db,sprintf('Cut-off point:\n(%.3f Hz, %.3f dB)',f_3db,mag_3db),...
    'VerticalAlignment','bottom','HorizontalAlignment','left')      %在目标坐标点处添加文字

示例图片如下