局部敏感哈希LSH（SimHash与MinHash）

SimHash

1.算法思想

假设我们有海量的文本数据，我们需要根据文本内容将它们进行去重。对于文本去重而言，目前有很多NLP相关的算法可以在很高精度上来解决，但是我们现在处理的是大数据维度上的文本去重，这就对算法的效率有着很高的要求。

而局部敏感hash算法可以将原始的文本内容映射为数字（hash签名），而且较为相近的文本内容对应的hash签名也比较相近。于是simhash算法就闪亮登场了，它是由 Charikar 在2002年提出来的，也是被Google公司进行海量网页去重的高效算法。

SimHash算法通过将原始的文本映射为64位 （可以根据实际情况调整，比如128位）的二进制数字串，然后通过比较二进制数字串的差异进而来表示原始文本内容的差异。

2.流程实现

整体流程主要分为以下五步：

（注：具体的事例摘自Lanceyan的博客《海量数据相似度计算之simhash和海明距离》）

• 分词

把需要判断文本分词形成这个文章的特征单词。最后形成去掉噪音词的单词序列并为每个词加上权重，我们假设权重分为5个级别（1~5）。

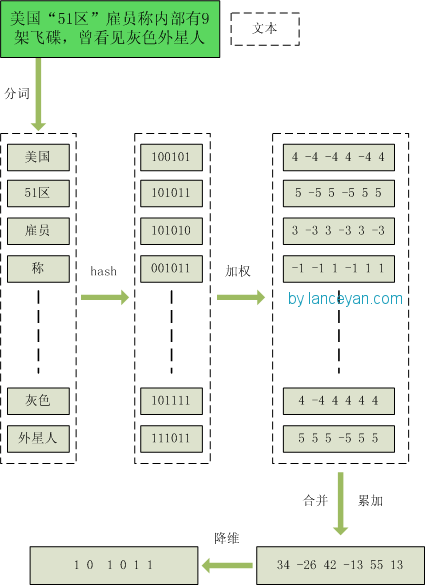
比如：“ 美国“51区”雇员称内部有9架飞碟，曾看见灰色外星人 ” ==> 分词后为 “ 美国（4） 51区（5） 雇员（3） 称（1） 内部（2） 有（1） 9架（3） 飞碟（5） 曾（1） 看见（3） 灰色（4） 外星人（5）”，括号里是代表单词在整个句子里重要程度，数字越大越重要。

• hash

通过hash算法把每个词变成hash值，比如“美国”通过hash算法计算为 100101,“51区”通过hash算法计算为 101011。这样我们的字符串就变成了一串串数字。

• 加权

通过 2步骤的hash生成结果，需要按照单词的权重形成加权数字串，比如“美国”的hash值为“100101”，通过加权计算为“4 -4 -4 4 -4 4”；“51区”的hash值为“101011”，通过加权计算为 “ 5 -5 5 -5 5 5”。

• 合并

把上面各个单词算出来的序列值累加，变成只有一个序列串。比如 “美国”的 “4 -4 -4 4 -4 4”，“51区”的 “ 5 -5 5 -5 5 5”， 把每一位进行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。这里作为示例只算了两个单词的，真实计算需要把所有单词的序列串累加。

• 降维

把4步算出来的 “9 -9 1 -1 1 9” 变成 0 1 串，形成我们最终的simhash签名。如果每一位大于0 记为 1，小于0 记为 0。最后算出结果为：“1 0 1 0 1 1”。

3.相似度计算 

我们把库里的文本都转换为simhash签名，并转换为long类型存储，空间大大减少，但是如何计算两个simhash的相似度呢？

难道是比较两个simhash的01有多少个不同吗？其实也就是这样，我们通过海明距离（Hamming distance）就可以计算出两个simhash到底相似不相似。两个simhash对应二进制（01串）取值不同的数量称为这两个simhash的海明距离。海明距离越小，相似度越大。

举例个例子：10101 和 00110 从第一位开始依次有第一位、第四、第五位不同，则海明距离为3。对于二进制字符串的a和b，海明距离为等于在a XOR b运算结果中1的个数（普遍算法）。

4.我们如何应用？

虽然simhash是针对文档去重的应用提出来的，但它的思想完全可以用在其他大规模规模样本的聚类上，我们只需要准备好特征及权重即可。在安全领域也不例外，比如针对恶意代码聚类，可以选取样本的多个特征，并为每个特征赋予经验权重。然后按照simhash算法的流程进行hash、加权、合并、降维，最后对每一个样本都生成对应的simhash签名。

这个时候问题来了，如果样本量大的话，两两对比simhash签名也是不小的工作量，为了解决这个问题，我们又使用了minhash进行分桶处理。

三、MinHash

1.算法思想

在数据挖掘中，一个最基本的问题就是比较两个集合的相似度。通常通过遍历这两个集合中的所有元素，统计这两个集合中相同元素的个数，来表示集合的相似度，也就是Jaccard相似度。

而minhash函数可以用来衡量原始集合之间的Jaccard相似度，因此可以用来快速估算两个集合的相似度。跟simhash一样，minhash也是LSH的一种，由Andrei Broder提出，最初用于在搜索引擎中检测重复网页，也可以应用于大规模聚类问题。

2.流程实现

假设集合A、B是两个特征向量：

• 使用一组随机的hash函数h(x)对集合A和B中的每个元素进行hash。

• hmin(A)、hmin(B)分别表示分别hash后集合A和集合B的最小值的向量。

• Jaccard距离来衡量相似度。

详情可参考这篇文章：

https://blog.csdn.net/liujan511536/article/details/47729721

3.我们如何应用？

既然minhash算法可以用来快速估算两个集合的相似度，那么我们就采用它来实现我们的分桶策略。接着前面应用部分的内容讲，我们对多个样本计算好simhash签名后，因为要两两比较相似度，样本多的情况下，计算量会比较大，这个时候minhash算法就闪亮登场了。

在得到每个样本的simhash签名后，采用minhash函数对它继续降维，将样本分入不同的桶中，然后再对同一个桶中的样本计算simhash相似度，这样既减少了计算量，又保证了准确性。