算法设计技术(编程珠玑)

算法设计技术

2010年10月3日星期日

20:53

#include <stdio.h>

#include <memory>

 

 

// 编程珠玑问题算法

typedefstruct

{

intst, ed, val;

}M;

 

voidsetM(M &m, int s, int e, int v)

{

m.st = s;

m.ed = e;

m.val = v;

}

 

voidcpyM(M &des, M &src)

{

des.st = src.st;

des.ed = src.ed;

des.val = src.val;

}

 

// 迭代算法，算法复杂度为O(N)

M FindMaxSubSet(int *a, intarray_size)

{

M *array_m = (M*)malloc(sizeof(M) * array_size);

int i;

 

setM(array_m[0], 0, 0, a[0]);

 

M _4ret = {0,0,a[0]};

 

for( i = 1; i <array_size; i++)

{

if(array_m[i - 1].val< 0)

{

setM(array_m[i], i, i, a[i]);

}

else

{

setM(array_m[i], array_m[i - 1].st, i, array_m[i - 1].val + a[i]);

}

 

if(array_m[i].val> _4ret.val)

                 {

cpyM(_4ret, array_m[i]);

}        

}

 

free(array_m ); array_m = 0;

 

return _4ret;

 

}

 

int main()

{

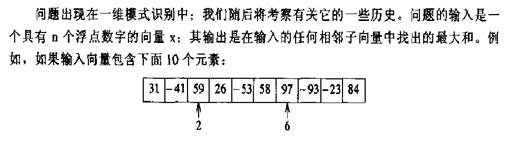
int A[] = {31, -41, 59, 26, -53, 58, 97, -93, -23, 84};

 

M m = FindMaxSubSet(A, sizeof(A) / sizeof(A[0]));

 

printf("l = %d, r = %d, val = %d\n", m.st, m.ed, m.val);

 

return 0;

}        

 

 

 

重要的算法设计技术：

保存状态，避免重复计算。算法2和4使用了简单的动态编程形式。通过使用一些空间来保存各个结果，我们就可以避免因重新计算而浪费时间。

   将信息预处理到数据结构中，算法2b中的cumarr结构允许对子向量中的总和进行快速计算。

    分治算法。算法3使用了简单的分治法形式;有关算法设计方面的教科书介绍了更多高级的分治法形式。

扫描算法。有关数组的问题经常可以通过询问“我如何可以将x[O..i-1 ]的解决方案扩展为x[0..i]的解决方案?”的方式得到解决。算法4同时保存旧的答案和一些辅助数据，以计算新答案。

累计。算法2b使用了累积表，在累积表中，第i个元素包含、中前i个值的总和;在处理范围时，这一类表很常见。例如，从本年初到10月份为止的销售额中减去本年初到2月份为止的销售额，业务分析师可以确定3月份到}D月份之间的销售额。

    下限。只有了解到他们的算法已经是可能算法中的最佳时，算法设计师才可能安安稳稳地睡个好觉。为此，他们必须证明某个匹配下限。本问题的线性下限就是问题6的主题，更加复杂的下限的求解可能会十分困难。算法复杂度计算