【基础算法】递归

一、递归是什么

递归是一种应用非常广泛的算法（或者变成技巧），很多算法的实现都需要依赖递归，比如，归并排序、快速排序、DFS 深度优先搜索、二叉树的前中后序遍历等。所以，搞懂递归非常重要。

简单来说，递归就是在函数中调用自己。递归求解问题分为“递”和“归” 2 个过程。

 

我们通过求整数 n 的阶乘来感受一下递归。

/**
 * 求整数 n 的阶乘
 *
 * @param n 整数
 * @return n 的阶乘
 */
public int factorial(int n) {
    if (n == 1) {
        return 1;
    }
    return n * factorial(n - 1);
}

首先，factorial 函数中调用自己，这是一个典型的递归函数。

其次，factorial 函数存在“递”和“归”2 个过程，先“递”再“归”。“递”的意思是将问题拆成子问题来解决，子问题再拆成子子问题 ... 直到被拆成的子问题无序再拆，即可以求解。“归”的意思是将最小的子问题解决了，那它的上一级子问题也就解决了，上上一级也就解决了 ... 直到最开始的问题解决。下图显示了 factorial(5) 的“递”和“归” 过程。

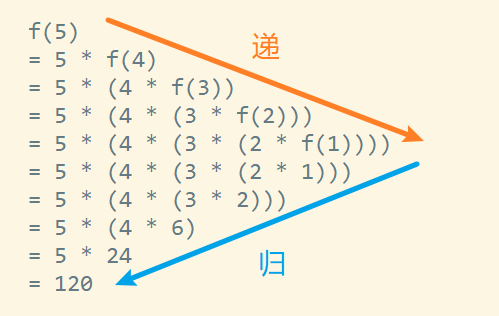
求解问题 f(5), 由于 f(5) = 5 * f(4), 所以 f(5) 需要拆成子问题 f(4) 进行求解，同理 f(4) = 4 * f(3) ,也需要进一步拆分 ... 直到 f(1), 这是“递”。f(1) 解决了，那 f(2) = 2 * f(1) = 2 * 1 = 1 也就解决了... f(5) 到最后也解决了，这是“归”。

递归的本质是逐步把问题拆分成具有相同解决思路的子问题，直到最后被拆成的子问题不能拆分，解决了最小粒度可求解的子问题后，在“归”的过程中自然而然地解决了最开始的问题。

 

二、递归的适用场景

同时满足以下 2 个条件的问题，都可以使用递归来解决。

1. 问题可以拆分成具有相同解决思路的子问题，也就是说这些问题都可以调用同一个函数来解决，而这个解决思路就是递推公式；
2. 经过层层拆分后，必然存在不能再拆分的固定值，即终止条件；否则，无穷无尽的拆分下去，问题显然是无解的。

 

比如，求整数 5 的阶乘，可以拆分为“5 * 4 的阶乘”，而 4 的阶乘求解思路与 5 的阶乘完全一样。最终，存在固定值“1 的阶乘 = 1”。

 

三、写递归代码的思路

写递归代码的关键是找到递推公式，确定终止条件，剩下将递推公式转化为代码就简单了。

 

我们通过走台阶例子看一下。假如有 n 个台阶，你每步可以跨 1 个台阶或者 2 个台阶，请编程求解走这 n 个台阶共有多少种走法。

第一，寻找递推公式，也就是寻找问题与子问题的关系。自上而下思考，因为每步可以跨 1 个台阶或者 2 个台阶，那么要走到第 n 个台阶，只能是走到第 n-1 个台阶再走一步（这一步跨 1 个台阶），或者走到第 n-2 个台阶再走一步（这一步跨 2 个台阶）。所以，走到第 n 个台阶的走法，就是走到第 n-1 个台阶的走法 加上 走到第 n-2 个台阶的走法。用公式表示为f(n) = f(n-1) + f(n-2)。

第二，确定终止条件。当只有 1 个台阶时，只有 1 种走法（一步跨 1 台阶）；当只有 2 个台阶时，只有 2 种走法（一步跨 1 个台阶，走 2 步；一步跨 2 个台阶，走 1 步）。用公式表示f(1) = 1, f(2) = 2。

 

把找到的递推公式和终止条件放到一起就是这样的：

// 终止条件
f(1) = 1;
f(2) = 2;

// 递推公式
f(n) = f(n-1) + f(n-2);

最终，转换成代码如下：

/**
 * 每步可以跨 1 个台阶或者 2 个台阶，求走 n 个台阶共有多少种走法
 *
 * @param n 台阶数量
 * @return 共有多少种走法
 */
public int walkNum(int n) {
    // 终止条件
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }

    // 递推公式
    return walkNum(n - 1) + walkNum(n - 2);
}

 

总结一下，写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。 

 

四、避免理解递归的思维误区

虽然说了这么多，但是可能还是有人感觉递归代码理解起来比较困难，其实大多数人都会有这种感觉。

刚讲的阶乘的例子，递归调用只有一个分支，也就是说“一个问题只需要分解为一个子问题”，我们很容易能够想清楚“递”和“归”的每一个步骤，所以写起来、理解起来都不难。

但是，当我们面对的是一个问题要分解为多个子问题的情况，递归代码就没那么好理解了。像刚讲的走台阶的例子，如果只有 3 个台阶，我们还能想明白每一种走法的每一步应该跨几个台阶，但是如果有 30 个台阶、300 个台阶，人脑几乎没办法把整个“递”和“归”的过程一步一步都想清楚。

计算机擅长做重复的事情，所以递归正符合它的胃口。而我们人脑更喜欢平铺直叙的思维方式。当我们看到递归时，总想把递归平铺展开，脑子里就会循环，一层一层往下调，然后再一层一层返回，试图想搞清楚计算机每一步都是怎么执行的，这样就很容易被绕进去。对于递归代码，试图想清楚整个递和归的过程，实际上是进入了一个思维误区。很多时候，我们理解起来比较吃力，主要原因就是自己给自己制造了这种理解障碍。

 

正确的思维方式应该是：如果一个问题 A 可以分解为子问题 B、C，我们可以假设子问题 B、C 已经解决，在此基础上思考如何解决问题 A。而且，只需要思考问题 A 与子问题 B、C 两层之间的关系即可，不需要一层一层往下思考子问题与子子问题，子子问题与子子子问题之间的关系。屏蔽掉递归细节，这样子理解起来就简单多了。

因此，编写递归代码的关键是，只要遇到递归，我们就把它抽象成一个递推公式，不用想一层层的调用关系，不要试图用人脑去分解递归的每个步骤。

 

五、递归代码常见问题

1.堆栈溢出

递归代码是在函数中调用自己，我们知道，函数调用会使用栈来保存临时变量，每调用一个函数，都会将临时变量封装为栈帧压入内存栈，等函数执行完成返回时，才出栈。系统栈或者虚拟机栈空间一般都不大。如果递归求解的数据规模很大，调用层次很深，一直压入栈，就会有堆栈溢出的风险。

比如，求 5 的阶乘，会调用函数 5 次，如果求 10000 的阶乘，会调用函数 10000 次，可能就会有堆栈溢出问题。

 

要避免堆栈溢出，可以在代码中对函数递归调用次数进行统计，超过一定调用次数让代码直接返回或者报错。也可以思考是否可以使用非递归的方式解决问题。

 

2.重复计算

递归代码可能会出现重复计算的问题，比如，走台阶的例子，如果我们把整个递归过程分解的话，就是下图所示的样子：

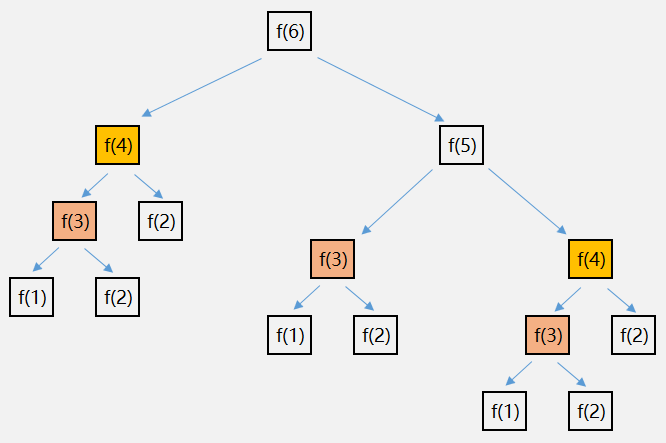
由图可知，计算 f(6) 的过程中，f(4) 被重复计算了 2 次，f(3) 被重复计算了 3 次。如果要计算 f(10) 重复计算的次数会更多。

 

为了避免重复计算，我们可以通过一个数据结构（比如散列表）来保存已经求解过的 f(k)。当递归调用到 f(k) 时，先看下是否已经求解过了。如果是，则直接从散列表中取值返回，不需要重复计算。

// key 是 n，value 是 f(n)
private Map<Integer, Integer> solvedMap = new HashMap<>();
    
/**
 * 每步可以跨 1 个台阶或者 2 个台阶，求走 n 个台阶共有多少种走法
 *
 * @param n 台阶数量
 * @return 共有多少种走法
 */
public int walkNum(int n) {
    // 终止条件
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }

    // 获取已经计算过的值，避免重复计算
    if (solvedMap.get(n) != null) {
        return solvedMap.get(n);
    }

    // 递推公式
    int res = walkNum(n - 1) + walkNum(n - 2);

    // 保存计算过的值
    solvedMap.put(n, res);
    return res;
}

 

改造后，避免了重复计算，但是由于我们保存了中间的计算结果，所以空间复杂度是 O(n)。可以将递归转为循环遍历来降低空间复杂度。

 

六、递归代码转为循环遍历

递归一般都是使用自上而下的分析方式，但是对于很多问题，我们可以转变思路，用自下而上的方式来解决。这样，就可以将递归代码转换为循环遍历，可以有效避免堆栈溢出、重复计算等问题。

 

比如，求整数阶乘的问题，通过自下而上的分析方法，我们发现：

f(1) = 1;
f(2) = 2 * f(1);
f(3) = 3 * f(2);
f(4) = 4 * f(3);
...
f(n) = n * f(n-1);

写成循环代码如下：

public static int factorial(int n) {
    int res = 1;
    for (int i = 2; i <= n; i++) {
        res *= i;
    }
    return res;
}

 

通过自下而上的方法分析走台阶的问题：

f(1) = 1;
f(2) = 2;
f(3) = f(1) + f(2);
f(4) = f(2) + f(3);
...
f(n) = f(n-2) + f(n-1);

写成循环代码如下：

public int walkNum(int n) {
    if (n == 1) {
        return 1;
    }
    if (n == 2) {
        return 2;
    }

    int res = 0;
    int prepre = 1;
    int pre = 2;
    for (int i = 3; i <= n; i++) {
        res = prepre + pre;
        prepre = pre;
        pre = res;
    }
    return res;
}