多层自编码器的微调
多层自编码器由多个稀疏自编码器和一个Softmax分类器构成;(其中,每个稀疏自编码器的权值可以利用无标签训练样本得到, Softmax分类器参数可由有标签训练样本得到)多层自编码器微调是指将多层自编码器看做是一个多层的神经网络,利用有标签的训练样本集,对该神经网络的权值进行调整。
1多层自编码器的结构
多层自编码器的结构如图1所示,它包含一个具有2个隐藏层的栈式自编码器和1个softmax模型;栈式自编码器的最后一个隐藏层的输出作为softmax模型的输入,softmax模型的输出作为整个网络的输出(输出的是条件概率向量)。
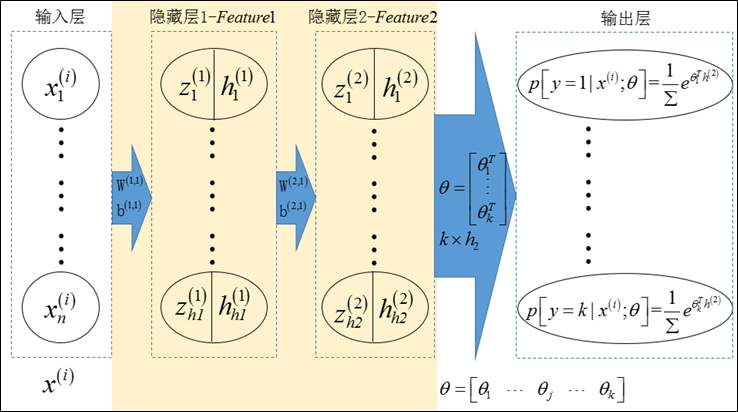
图1 多层自编码器的结构
微调多层自编码器的流程图如图2所示,该流程主要包括三部分:
(1)初始化待优化参数向量
(2)调用最优化函数,计算最优化参数向量
(3)得到最优化参数向量,可以转换为网络各结构所对应的参数
其中,最小化代价函数主要利用minFunc函数,该优化函数格式如下:

可知,为了实现优化过程,最为关键问题就是编写stackedAECost函数

图2 多层自编码器的微调流程
2整个网络参数的初始化
整个网络的参数stackedAETheta(列向量形式)由两部分组成:softmax分类器参数向量+稀疏自编码器参数向量;他们的初始化值由稀疏自编码和softmax学习获得:


3 stackedAECost函数
3.1稀疏自编码器部分的激励值
3.1.1 稀疏自编码器部分的结构图
多层网络的稀疏自编码器部分如下图所示
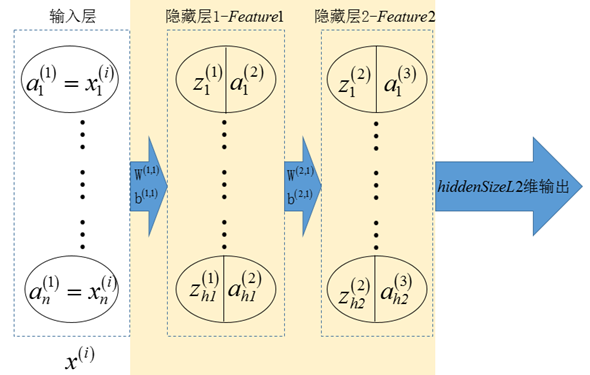
图3 多层网络的稀疏自编码器部分
3.1.2 稀疏自编码器部分各层激励值(输出)
|
单个样本 |
多个样本 |
|
|
|
3.1.3 softmax分类器的激励值(输出)
|
单个样本 |
多个样本 |
|
|
|
3.1.4 程序

3.2代价函数
3.2.1代价函数的计算公式
该多层网络的代价函数完全按照softmax模型的代价函数计算,并加入正则项,但要注意,这里加入的正则项必须要对整个网络的所有参数进行惩罚!
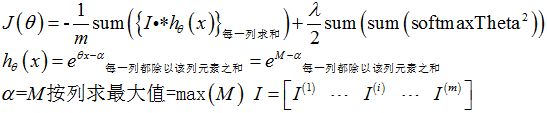
3.2.2程序如下

3.3梯度计算
3.3.1 softmax模型
该模型的梯度计算与单独使用softmxa模型的公式是相同的,即:
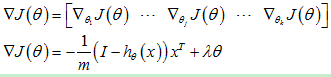
只不过这里的x为softmax自编码器最后一层的输出h(2)。

3.1.2 stack自编码器各层
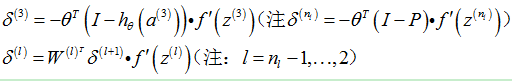
|
单个样本 |
多个样本 |
|
|
|
3.3.3 整个网络的梯度
最后,将整个网络的梯度(softmaxThetaGrad和stackgrad)存放在一个列向量中



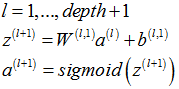
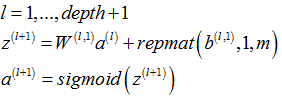
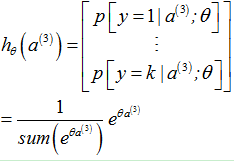
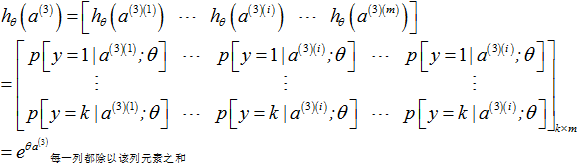
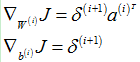
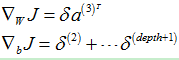

 浙公网安备 33010602011771号
浙公网安备 33010602011771号