卷积神经网络 cnnff.m程序 中的前向传播算法 数据 分步解析
最近在学习卷积神经网络,哎,真的是一头雾水!最后决定从阅读CNN程序下手!
程序来源于GitHub的DeepLearnToolbox
由于确实缺乏理论基础,所以,先从程序的数据流入手,虽然对高手来讲,这样有点太小儿科了,但觉得对于个人理解CNN网络的结构和数据流走向有较大帮助!
下面,将要分析CNN的前向传播算法cnnff.m
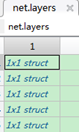
本程序所用的神经网络的结构如下图的结构体net所示
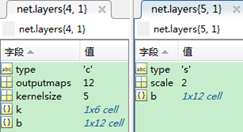
| 结构体net | 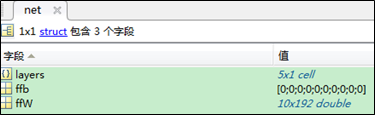 |
|
包含5层
|
每层的结构
|
这五层的结构如下:
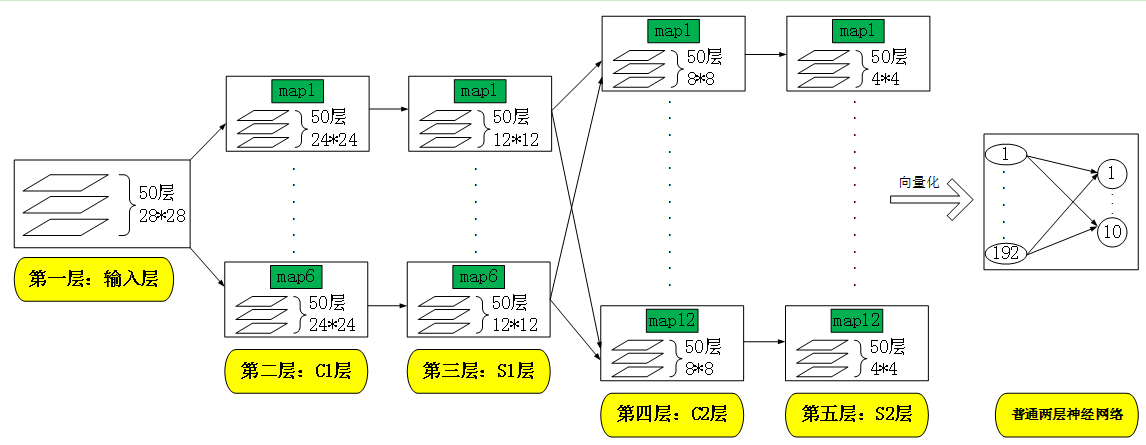
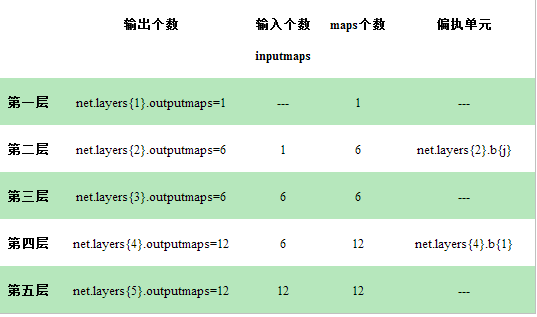
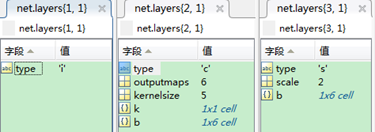
每层的结构分别如下:
为了方便自己理解,下面,分别对每一层的输入、输出、传播分解介绍
只考虑某一批词的样本
注:所有样本集被分为numbatches批,每一批含有batchsize个样本,对于本程序而言,共有50个样本
1 第一层到第五层的数据传递

2 第1层到第2层的前面传播(l=2):卷积操作

利用循环,分别计算第二层每个map的输出:net.layers{2}.a{j} (j=1,..,6)(这里的l=2)

(1)初始化一个三维矩阵z
-
z的大小为24*24*50,即第二层中每个map的尺寸
-
z存放的是:第二层中每个map的输入
(2)计算第2层第j个map的输入
-
即第1层的所有输出(i=1,…, inputmaps)对第2层的第j个输入的贡献的累加
-
z的计算方法是:
利用第二层的第j个map的卷积核net.layers{2}.k{i}{j}分别对第一层中的第i个map进行卷积运算(i=1,…, net.layers{1}.outputmaps),并将得到的所有卷积结果相加
![]()
-
第2层的inputmaps=1
-
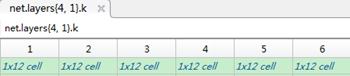
对net.layers{l}.k{i}{j}进行解释:
|
net.layers{l}.k:是一个元胞,有两层 net.layers{l}.k{i}:第l-1层的第i个map到第l层的所有maps的卷积核 net.layers{l}.k{i}{j}:第l-1层的第i个map到第l层的第j个map的卷积核 下面是一个例子: 第四层的卷积核元胞
第3层的第1个map到第4层的所有maps的卷积核(12)个
第3层的第1个map到第四层的第1个maps的卷积核
|
(3)计算第2层的第j个map的输出
-
第二层的第j个map的输出为net.layers{2}.a{j}=sigm(z+net.layers{l}.b{j})
即第二层的第j个map的输入z+该map的偏执项后,求sigm函数
(4)对第1层的map进行卷积操作的图例
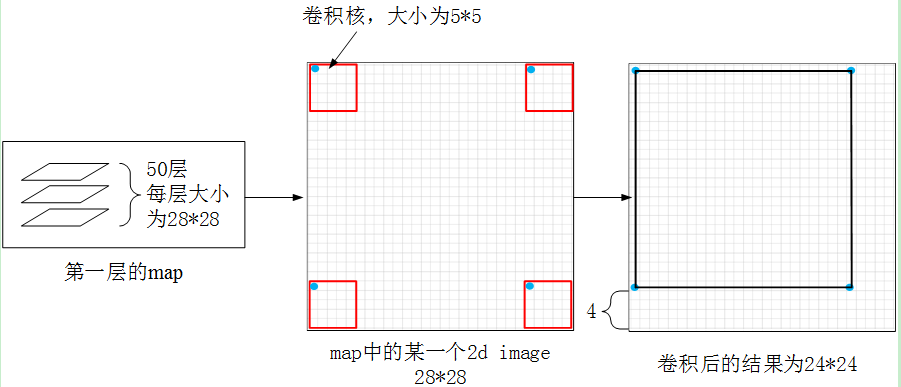
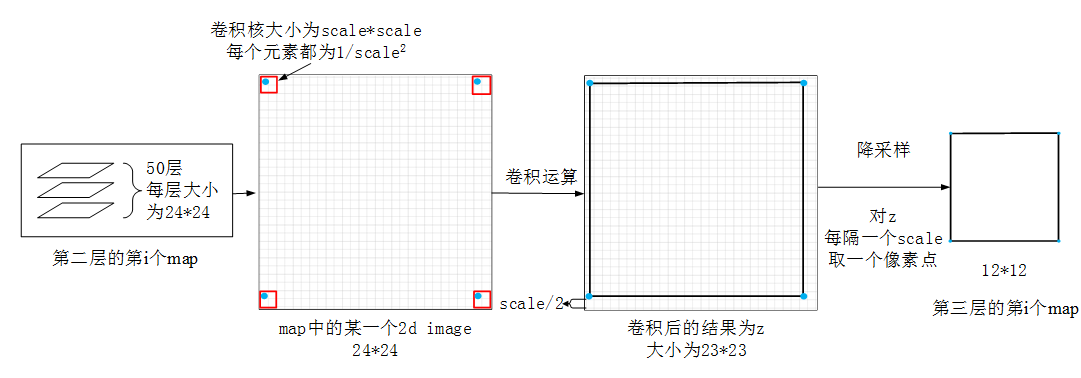
3 第2层到第3层(l=3):降采样操作


下面,讨论第j次循环时,循环体内部的分步解析
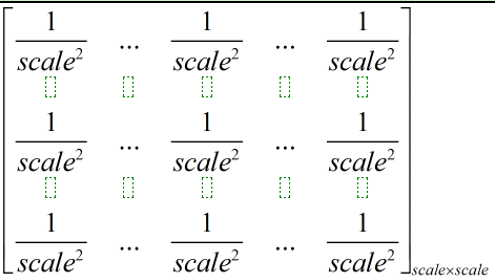
(1)对第二层的第j个map进行卷积运算,得到z
-
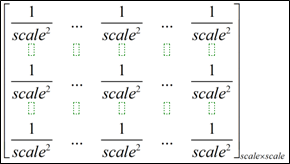
利用的卷积核(大小为scale*scale)如下:
![]()
(2)对z进行降采样,得到第三层的第j个map的输出
(3)如上所示的降采样过程示例如下图所示
4 第3层到第4层的前面传播(l=4):卷积操作
利用循环,分别计算第四层每个map的输出:net.layers{4}.a{j} (j=1,..,12)(这里的l=4)

下面,讨论第j次循环时,循环体内部的分步解析
(1)初始化一个三维矩阵z
-
z的大小为24*24*50,即第二层中每个map的尺寸
-
z存放的是:第四层中每个map的输入
(2)计算第4层的第j个map的输入
-
即第3层的所有输出(i=1,…, inputmaps)对第4层的第j个输入的贡献的累加
-
z的计算方法是:
利用第4层的第j个map的卷积核net.layers{4}.k{i}{j}分别对第3层中的第i个map进行卷积运算(i=1,…, net.layers{1}.outputmaps),并将得到的所有卷积结果相加
![]()
-
第4层的inputmaps=12
(3)计算第4层的第j个map的输出
-
第4层的第j个map的输出为net.layers{4}.a{j}=sigm(z+net.layers{4}.b{j})
即第4层的第j个map的输入z+该map的偏执项后,求sigm函数
(4)对第3层的map进行卷积操作的图例

5 第4层到第5层 (l=5):降采样
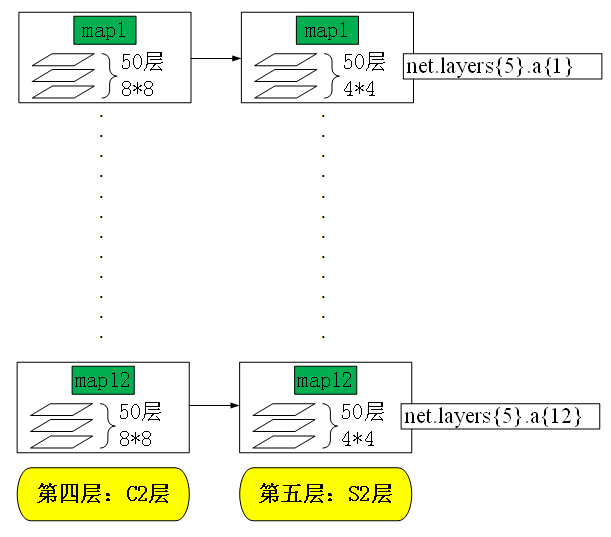

下面,讨论第j次循环时,循环体内部的分步解析
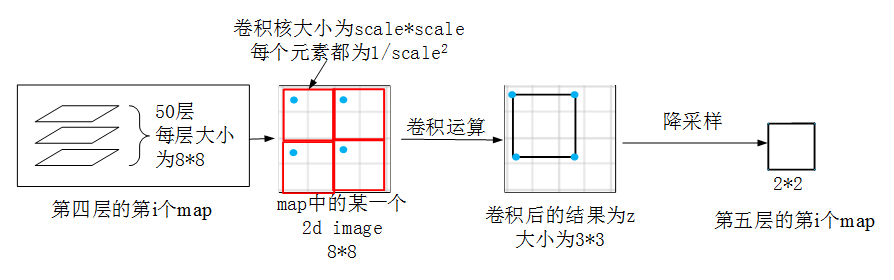
(1)对第四层的第j个map进行卷积运算,得到z
-
利用的卷积核(大小为scale*scale)如下:
![]()
(2)对z进行降采样,得到第五层的第j个map的输出
6 将第五层的map输出向量化
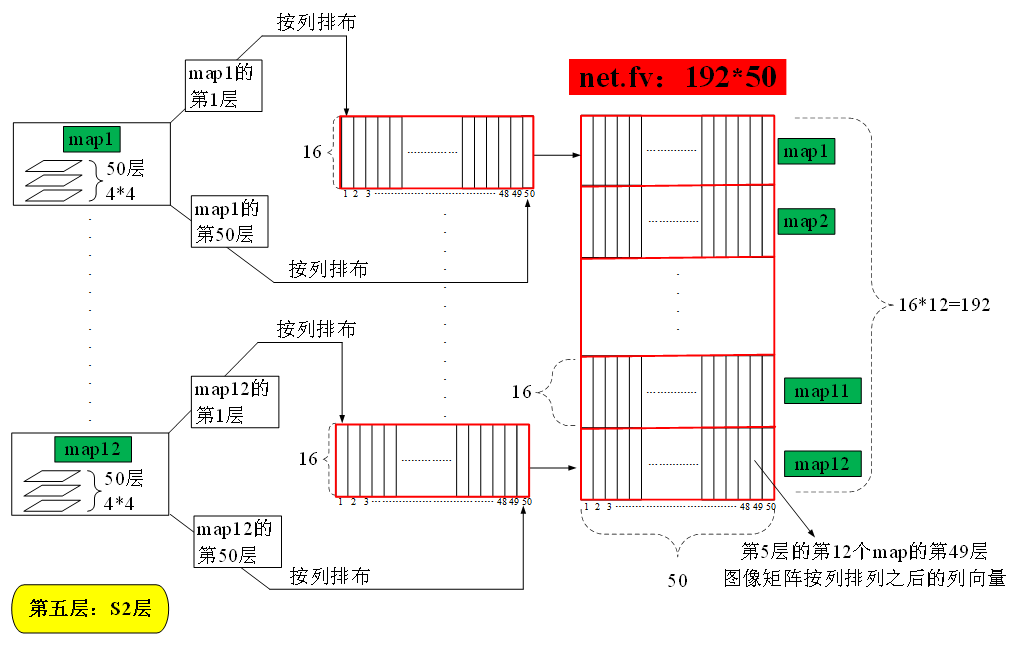

(3)对于第五层的第j个输出map
-
得到第五层第j个输出map的尺寸,应该是三维的,得到的三维尺寸向量存入sa中
-
将第五层的第j个输出map的矩阵转化为一个sa(1)*sa(2),sa(3)大小的矩阵
-
并将该得到的转化矩阵接入到第五层的第j-1个输出map之后
-
关于矩阵fv的结构如上图所示
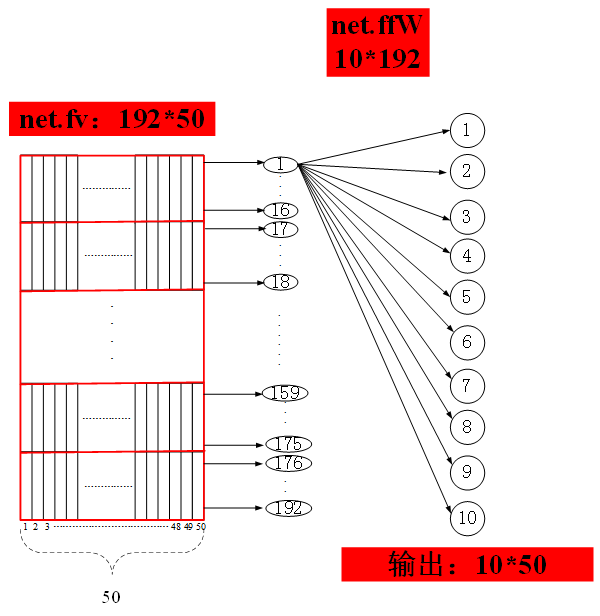
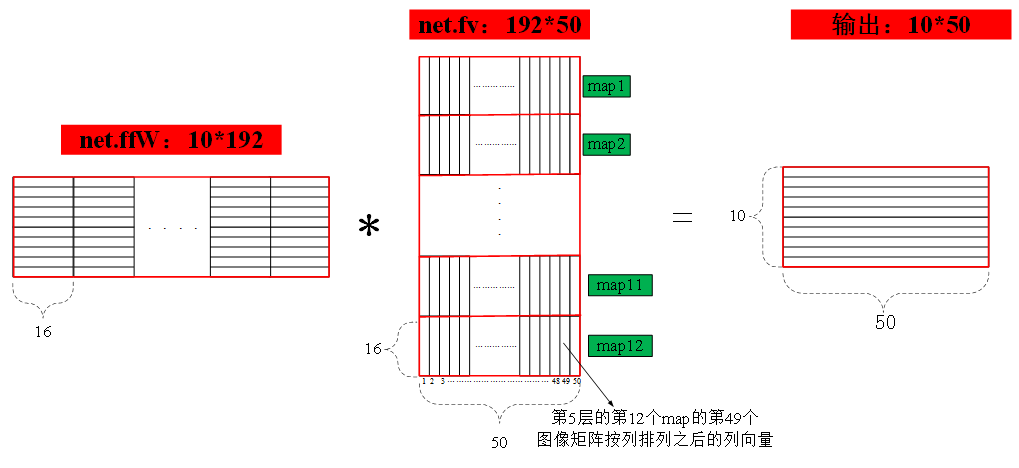

第五层的向量化输出传入一个普通的神经网络,只有输入层和输出层,输入层含有192个神经元,输出层含有10个神经元,输入到输出层的权值矩阵存放在矩阵net.ffW中,在该权值矩阵作用下,该简单神经网络的输出即为最终的整个网络的输出,输出结果存放在net.o矩阵中,该矩阵大小为10*50,每一列分别表示每个输入样本得到的相应的输出


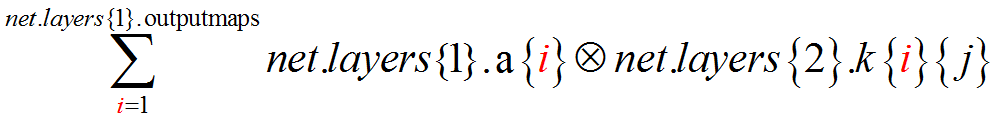


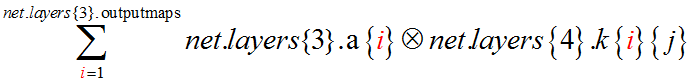

 浙公网安备 33010602011771号
浙公网安备 33010602011771号