思考:对一亿个int型整数排序,哪种排序算法效率最高?
下图是常见排序算法的最好,最坏,平均时间复杂度、空间复杂度,稳定性总结表。

直接看表格,综合时间复杂度、空间复杂度等各种因素,目测堆排序是最优选择。不管最好、最坏还是平均情况,时间复杂度都是O(nlogn),而且还不像快排排序和归并排序那样占空间,计数排序、基数排序、桶排序空间复杂度太大,需要消耗大量额外空间。
快速排序和堆排序
接下来亲自比较一下,快速排序和堆排序到底谁效率更高。附上快速排序和堆排序的代码(其中,快速排序使用《编程珠玑》第二版第11章中的方法,堆排序使用第14章中的方法)。
//快速排序
void swap(int*a, int*b){
int temp = *a;
*a = *b;
*b = temp;
}
void quicksort(int *a, int l, int u){
if (l >= u) return;
srand(time(NULL));
int j = (rand() % (u - l + 1)) + l;
swap(&a[l], &a[j]);
int m = a[l];
int index = u + 1;
for (int i = u; i >= l; i--)
{
if (a[i] >= m)
swap(&a[i], &a[--index]);
}
quicksort(a, l, index - 1);
quicksort(a, index + 1, u);
}
//堆排序
vector<int> x;
void swap(int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}
void siftup(int n){
int i, p;
for (i = n; i > 1 && x[p = i / 2] > x[i]; i = p) {
swap(&x[i],&x[p]);
}
}
void siftdown(int n)
{
int i, c;
for (i = 1; (c = 2 * i) <= n; i = c)
{
if (c + 1 <= n && x[c + 1] < x[c])c++;
if (x[i] <= x[c])break;
swap(&x[i],&x[c]);
}
}下面是本人在自己电脑上测试的结果,win7系统,i7 7代CPU,8G内存。
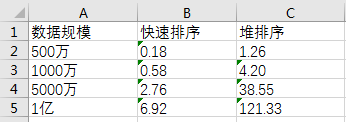
不比不知道,一比吓一跳,数据规模越大,快速排序的优势越来越大,Why??? 难道只从复杂度角度判断算法优劣有问题???
从复杂度角度判断算法其实也没什么问题,只能说是想的太少了,结合到实际的内存存储问题,数据频繁交换、写入、移除、调整等问题,堆排序要大很多。
在堆排序(小根堆)的时候,每次总是将最小的元素移除,然后将最后的元素放到堆顶,再让其自我调整。这样一来,有很多比较将是被浪费的,因为被拿到堆顶的那个元素几乎肯定是很大的,而靠近堆顶的元素又几乎肯定是很小的,最后一个元素能留在堆顶的可能性微乎其微,最后一个元素很有可能最终再被移动到底部。在堆排序里面有大量这种近乎无效的比较。随着数据规模的增长,比较的开销最差情况应该在(线性*对数)级别,如果数据量是原来的10倍,那么用于比较的时间开销可能是原来的10log10倍。
堆排序的过程中,需要有效的随机存取。比较父节点和字节点的值大小的时候,虽然计算下标会很快完成,但是在大规模的数据中对数组指针寻址也需要一定的时间。而快速排序只需要将数组指针移动到相邻的区域即可。在堆排序中,会大量的随机存取数据;而在快速排序中,只会大量的顺序存取数据。随着数据规模的扩大,这方面的差距会明显增大。在这方面的时间开销来说,快速排序只会线性增长,而堆排序增加幅度很大,会远远大于线性。
在快速排序中,每次数据移动都意味着该数据距离它正确的位置越来越近,而在堆排序中,类似将堆尾部的数据移到堆顶这样的操作只会使相应的数据远离它正确的位置,后续必然有一些操作再将其移动,即“做了好多无用功”。
在《编程珠玑》一书中,编者建议我们使用C/C++标准函数库中的sort函数。
C++标准库里的sort()函数
为什么要用c++标准库里的排序函数?
Sort函数包含在头文件为#include<algorithm>的c++标准库中,调用标准库里的排序方法可以不必知道其内部是如何实现的,只要出现我们想要的结果即可!
Sort()函数是c++一种排序方法之一,学会了这种方法也打消我学习c++以来使用的冒泡排序和选择排序所带来的执行效率不高的问题!貌似它是使用者的输入数据来选择最优的排序算法,执行效率较高!
sort函数有三个参数:
(1)第一个是要排序的数组的起始地址。
(2)第二个是结束的地址(最后一位要排序的地址)
(3)第三个参数是排序的方法,可以是从大到小也可是从小到大,还可以不写第三个参数,此时默认的排序方法是从小到大排序。
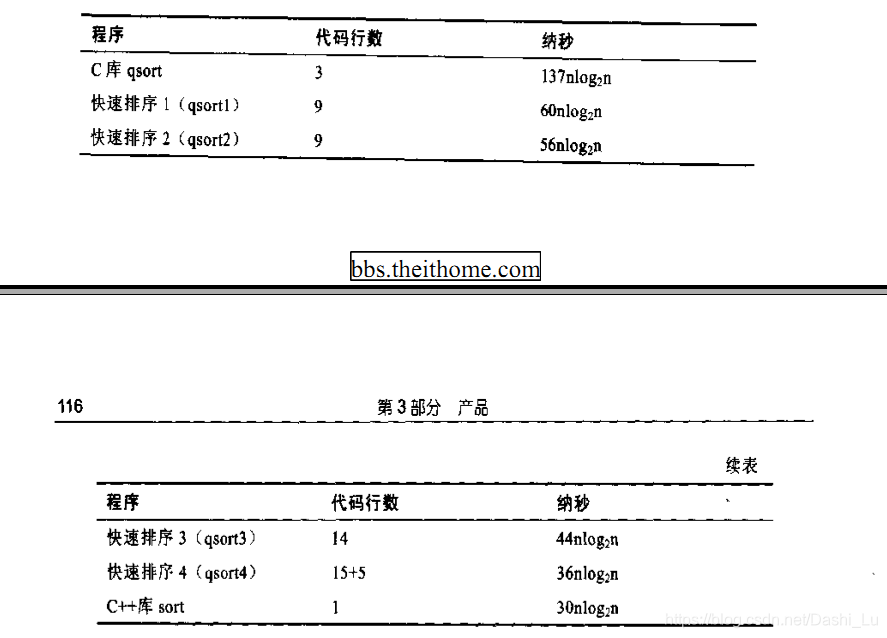
(参考《编程珠玑》第二版第11章)
进击的排序
我在某论坛里看到有人提到使用位图排序,稍微看了一下,没有仔细研究!
贴上网上抄袭的电话号码排序问题实现算法。
#include <iostream>
#include <cstdlib>
#include <ctime>
#include <bitset>
using namespace std;
void randInt(int n, int m, int arrayM[])
{
srand(time(0));
int *arrayN = new int[n];
for (int i = 0; i < n; i++)
arrayN[i] = i + 1;
for (int i = 0; i < n; i++) {
int temp, rint;
rint = rand() % n;
temp = arrayN[i];
arrayN[i] = arrayN[rint];
arrayN[rint] = temp;
}
for (int i = 0; i < m; i++)
arrayM[i] = arrayN[i];
}
int main(){
int n = 10, m = 5;
int *arrayM = new int[m];
randInt(n, m, arrayM);
cout << "orginal number: ";
for (int i = 0; i < m; i++)
cout << arrayM[i] << " ";
cout << endl;
bitset<10> abit;
abit.reset();
for (int i = 0; i < m; i++)
abit.set(arrayM[i] - 1);
cout << "sorted number: ";
for (int i = 0; i < n; i++)
if (abit.test(i))
cout << i + 1 << " ";
cout << endl;
return 0;
}参考文献:《编程珠玑》第二版


