树(二叉树)
前面学过的数据结构，包括向量、链表、栈、队列，从物理上或者逻辑上来说，存在一定的前后次序，并且前驱和后继是唯一的，因此称之为线性结构。然而，向量的插入和删除操作、链表的循秩访问等操作，复杂度都非常高。树的结构，可以把两种结构的优势结合起来。
与前两种结构不同，树不存在天然的直接后继或者直接前驱关系，不过，我们可以通过定义一些约束，在树中确定节点之间的线性次序。树属于半线性结构。从结构来看，树其实是一种特殊的图，等价于连通无环图。与图一样，树也由一组顶点以及之间的联边组成，外加指定一个特定的根节点。
树的几个概念
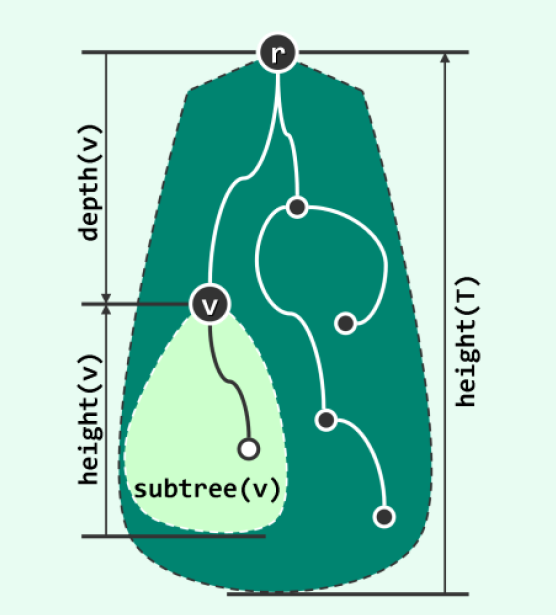深度(depth)：如图所示，根节点为r，v是一个树中间的节点。v的深度，即为v到r的唯一通路经过的边的个数，记作depth(v)。
祖先(ancestor)、后代(descendant)：任一节点v在通往树根沿途所经过的每个节点都是其祖先，v是他们的后代。特别地，如果u恰好比v高一层，则u是v的父亲(parent)，v是u的孩子(child)。
度数(degree)：v孩子的个数，称为v的度数，记作deg(v)。
叶节点(leaf)：如果节点v没有后代，那么v称为叶节点。
子树(subtree)：v及其后代，以及他们直接的联边，称为一颗子树，记作subtree(v)。
高度(height)：树T中所有节点深度的最大值，称作该树的高度，记作height(T)，推广这一定义，节点v对应子树的高度，记作height(v)。
二叉树
如果每个节点最多有两个孩子，即每个节点的度数均不超过2，称为二叉树(binary tree)。
二叉树中，如果同一节点的孩子以左右区分，称为有序二叉树(ordered binary tree)。特别地，不含一度节点的二叉树称作真二叉树(proper binary tree)。二叉树是不失一般性地，比如一个多叉树，如果可以定义兄弟节点的次序，那么可以转换为一颗二叉树。比如，假设每个节点有两个指针，一个指向“长子”，一个指向下一个兄弟，那么这颗多叉树就转化为了一颗二叉树，如下如所示：
二叉树的实现与遍历
下面，简单定义一个二叉树节点的模板类:
1 template<typename T> class BinNode { 2 public: 3 T data; 4 BinNodePosi(T) parent; 5 BinNodePosi(T) lc; BinNodePosi(T) rc; 6 int height; 7 // 构造函数 8 BinNode() :parent(nullptr), lc(nullptr), rc(nullptr), height(0) {} 9 BinNode(T e, BinNodePosi(T) p = nullptr, BinNodePosi(T) lc = nullptr, BinNodePosi(T) rc = nullptr,int h = 0) : 10 data(e), parent(p), lc(lc), rc(rc), height(h){} 11 // 操作接口 12 int size();//返回以该节点作为根节点的子树规模 13 BinNodePosi(T) insertAsLC(T const&); 14 BinNodePosi(T) insertAsRC(T const&); 15 BinNodePosi(T) succ();//直接后继 16 17 }; 18 template<typename T> BinNodePosi(T) BinNode<T>::insertAsLC(T const& e) 19 { 20 return lc = new BinNode(e, this); 21 } 22 template<typename T> BinNodePosi(T) BinNode<T>::insertAsRC(T const& e) 23 { 24 return rc = new BinNode(e, this); 25 }
二叉树的模板类：
1 template<typename T> int stature(BinNodePosi(T) p) 2 { 3 return (p) ? (p)->height : -1; 4 } 5 template<typename T> class BinTree { 6 protected: 7 int _size; BinNodePosi(T) _root; 8 virtual int updateHeight(BinNodePosi(T) x);//更新节点x的高度 9 void updateHeightAbove(BinNodePosi(T) x);//更新节点及其祖先的高度 10 public: 11 BinTree() :_size(0), _root(NULL) {} 12 ~BinTree() { if (_size > 0) remove(_root); } 13 int size() const { return _size; } 14 bool empty()const { return !_root; } 15 BinNodePosi(T) root() const { return _root; } 16 BinNodePosi(T) insertAsRoot(T const& e); 17 BinNodePosi(T) insertAsLC(BinNodePosi(T) x,T const& e); 18 BinNodePosi(T) insertAsRC(BinNodePosi(T) x, T const& e);//x原来没有LC||RC 19 BinNodePosi(T) attachAsLC(BinNodePosi(T) x, BinTree<T>*& T);//T作为x的子树接入 20 BinNodePosi(T) attachAsRC(BinNodePosi(T) x, BinTree<T>*& T); 21 int remove(BinNodePosi(T) x);//删除x为根的子树 22 BinTree<T>* secede(BinNodePosi(T) x);//删除子树，并作为新树返回根节点 23 }; 24 int max(int a, int b) { return a > b ? a : b; } 25 template<typename T> int BinTree<T>::updateHeight(BinNodePosi(T) x) 26 { 27 return x->height = 1 + max(stature(x->lc), stature(x->rc)); 28 } 29 template<typename T> void BinTree<T>::updateHeightAbove(BinNodePosi(T) x) 30 { 31 while (x) 32 { 33 updateHeight(x); x = x->parent; 34 } 35 } 36 template<typename T> BinNodePosi(T) BinTree<T>::insertAsRoot(T const& e) 37 { 38 _size = 1; 39 return _root = new BinNode<T>(e); 40 } 41 template<typename T> BinNodePosi(T) BinTree<T>::insertAsLC(BinNodePosi(T) x, T const& e) 42 { 43 _size++; x->insertAsLC(e); updateHeightAbove(x); return x->lc; 44 } 45 template<typename T> BinNodePosi(T) BinTree<T>::insertAsRC(BinNodePosi(T) x, T const& e) 46 { 47 _size++; x->insertAsRC(e); updateHeightAbove(x); return x->rc; 48 } 49 template<typename T> BinNodePosi(T) BinTree<T>::attachAsLC(BinNodePosi(T) x, BinTree<T>*& S) 50 { 51 x->lc = S->_root; S._root->parent = x; 52 _size += S->_size; updateHeightAbove(x); 53 S->_root = NULL; S->_size = 0; release(S); S = NULL; return x; 54 } 55 template<typename T> BinNodePosi(T) BinTree<T>::attachAsRC(BinNodePosi(T) x, BinTree<T>*& S) 56 { 57 x->rc = S->_root; S._root->parent = x; 58 _size += S->_size; updateHeightAbove(x); 59 S->_root = NULL; S->_size = 0; release(S); S = NULL; return x; 60 } 61 template<typename T> int BinTree<T>::remove(BinNodePosi(T) x) 62 { 63 FromParentTo(*(x)) = NULL;//切断parent->x 64 updateHeightAbove(x->parent); 65 int n = removeAt(x); _size -= n; return n; 66 } 67 template<typename T> static int removeAt(BinNodePosi(T) x)//删除位置x处的节点及其后代，返回被删除节点的值 68 { 69 if (!x) return 0; 70 int n = 1 + removeAt(x->lc) + removeAt(x->rc); 71 //release(x->data); release(x); 72 return n; 73 } 74 template<typename T> BinTree<T>* BinTree<T>::secede(BinNodePosi(T) x) 75 { 76 FromParentTo(*x) = NULL; updateHeightAbove(x->parent); 77 BinTree<T>* S = new BinTree<T>; S->_root = x; x->parent = NULL;//以x为根节点新建树 78 S->_size = x->size(); _size -= S->_size; return S; 79 }
只包含了一些简单的功能，比如插入节点，返回树的根节点，删除节点以及以该节点为根节点的子树、接入一颗子树、子树分离等操作。需要考虑的地方都比较类似，一定不要忘记更新操作后祖先的高度，以及树的规模。
树的遍历
树的遍历是非常重要的部分，如果能确定一个先后次序，就可以像访问链表一样，方便地对存储的数据进行操作。常见的遍历，包括先序遍历、中序遍历、后续遍历以及层次遍历，他们的访问次序如下图所示：
几种遍历的递归方法
递归方法是比较简单的，根据几种遍历的规则，可以简单地得出，以先序遍历为例：
1 template<typename T> void travPre(BinNodePosi(T) x) 2 { 3 if (!x) return; 4 visit(x); 5 travPre(x->lc); 6 travPre(x->rc); 7 }
先访问父节点，再递归地访问左孩子和右孩子，另外两种遍历也类似。
迭代方法
1 template<typename T> void travPre(BinNodePosi(T) x)//子树中序遍历 2 { 3 stack<BinNodePosi(T)> s; 4 while (1) 5 { 6 while (x) 7 { 8 visit(x); 9 if (x->rc) s.push(x->rc); 10 x = x->lc; 11 } 12 if (s.empty()) break; 13 x = s.top(); 14 s.pop(); 15 } 16 } 17 template<typename T> void travIn_v1(BinNodePosi(T) x) 18 { 19 stack<BinNodePosi(T)> s; 20 while (1) 21 { 22 while (x) 23 { 24 s.push(x); 25 x = x->lc; 26 } 27 if (s.empty()) break; 28 x = s.top(); 29 visit(x); 30 s.pop(); 31 x = x->rc; 32 } 33 } 34 template<typename T> BinNodePosi(T) BinNode<T>::succ() 35 { 36 BinNodePosi(T) s = this; 37 if (rc) 38 { 39 s = rc; 40 while (s->lc) s = s->lc;//若有右孩子，后继为右子树最深处最靠左的节点 41 } 42 else//否则，直接后继应当为将当前节点包含于其左子树中的最低祖先 43 { 44 while ((s->parent)&&(s->parent->rc==s)) s = s->parent;//若s为右孩子， 45 s = s->parent; 46 } 47 return s; 48 } 49 template<typename T> void travIn_v2(BinNodePosi(T) x)//不需要辅助栈的中序遍历 50 { 51 bool backtrack = false; 52 while (true) 53 if (!backtrack && (x->lc))//当不是刚刚回溯的并且有左子树 54 x = x->lc; 55 else //刚刚回溯或者没有子树 56 { 57 visit(x); 58 if (x->rc)//如果右子树非空 59 { 60 x = x->rc; 61 backtrack = false; 62 } 63 else 64 { 65 if (!(x = x->succ())) break;//回溯(包括了抵达末节点时的退出) 66 backtrack = true; 67 } 68 } 69 } 70 template<typename T> void travPost(BinNodePosi(T) x) 71 { 72 stack<BinNodePosi(T)> S; 73 if (x) S.push(x);//根节点入栈 74 while (!S.empty()) 75 { 76 if (S.top() != x->parent)//栈顶若不是当前节点的父亲，则必定是其右兄弟(右孩子先入栈，右为空时，栈顶为其父亲) 77 {//若栈顶为当前访问元素的父亲，则直接访问不需要继续搜索 78 while (BinNodePosi(T) x = S.top())//从栈顶出发，寻找栈顶节点的左右孩子 79 if (x->lc)//当有左孩子的时候，尽量向左 80 { 81 if (x->rc) S.push(x->rc);//若有右孩子，先入栈 82 S.push(x->lc);//然后把左孩子也入栈 83 } 84 else//若当前节点只有右孩子(可能不存在为空) 85 S.push(x -> rc); 86 S.pop();//退出循环时，栈顶为空，弹出这个空节点 87 } 88 x = S.top(); 89 S.pop(); 90 visit(x);//栈顶节点出栈并访问 91 } 92 } 93 template<typename T> void travLevel(BinNodePosi(T) x) 94 { 95 queue<BinNodePosi(T)> q; 96 q.push(x); 97 while (!q.empty()) 98 { 99 BinNodePosi(T) n = q.front(); q.pop(); visit(n); 100 if (n->lc) q.push(n->lc); 101 if (n->rc) q.push(n->rc); 102 } 103 }
对于先序遍历，在递归中我们也可以看到，属于尾递归，故一定可以修改得到迭代方法。在这里，我们采用了一个辅助栈的方法，借助栈来记录下一个要访问的节点。
对于中序遍历，延续先序遍历的方法，也给出了一种不需要辅助栈的方法，代价是我们需要定义一个函数，每次寻找后继节点。事实上，通过使用直接后继的方法，中序遍历可以无需借助辅助栈以及标志位来实现。
后序遍历的复杂程度要超过前两种，并且一定无法从递归得来，也通过使用辅助栈解决。
对于层次遍历，方法最为简单明了。借助队列，每次访问节点，将其孩子入队，下次循环出队列，即可按照层次访问。
最后，区分一下几种二叉树。
完全二叉树：在对某棵二叉树层次遍历的过程中，如果前[n/2](向下取整)次迭代中都有左孩子入队，且前[n/2](向上取整)-1次迭代中都有右孩子入队，则称为完全二叉树(complete binary tree)。完全二叉树简单来说，就是最后一层左侧必须有节点，而右侧可以有空缺，有如下宏观特征：叶节点只能出现在最底部的两层，并且最底层叶节点均处于次底层叶节点的左侧。因此，高度为h的完全二叉树，节点数应在2^h到2^(h+1)-1之间，反之，规模为n的完全二叉树，高度h=log[log2n](向下取整)。叶节点虽不至于少于内部节点，但最多多出一个。
满二叉树：完全二叉树的一种特殊情况，所有叶节点同处于最底层，每一层的节点数都达到饱和，称为满二叉树。
二叉树的向量实现
有了完全二叉树的概念，我们可以在二叉树的层次遍历中，得出一种二叉树节点的新组成形式。因为完全二叉树的特性，内部节点均为二度节点，因此，父节点与子节点间存在一定的数量关系，可以在层次遍历时，把二叉树组织为一个向量结构，从而便于进行访问和修改。具体关系如下:
假设一个节点的序号(秩)为r(x)，则他的左孩子序号为2*r(x)+1，右孩子序号为2*r(x)+2。通过二进制展开也可以判断父子关系，一个节点是另外一个节点的祖先，当且仅当二进制展开是它的前缀。特别地，|S(A)|+1=|S(D)|时，为父子关系。
以向量实现的二叉树，层次遍历只需要从前到后进行。其它几种遍历方式与前面的实现原理上相同，不同之处仅在于，节点是普通的向量元素，不再存在父子指针。因此，可以通过将父子指针修改为上面提到的秩的关系，即可实现各种遍历。
ps:文中的图片选自邓俊辉老师《数据结构(C++语言版)》。
