随机梯度下降法(SGD)

梯度下降法

大多数机器学习或者深度学习算法都涉及某种形式的优化。优化指的是改变特征x以最小化或最大化某个函数f(x)的任务。我们通常以最小化f(x)指代大多数最优化问题。最大化可经由最小化算法最小化-f(x)来实现。

我们要把最小化或最大化的函数称为目标函数或准则。当我们对其进行最小化时，我们也把它称为损失函数或误差函数。

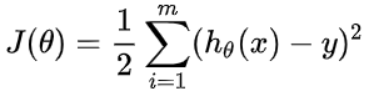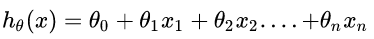下面，我们假设一个损失函数为,其中然后要使得最小化它。

 

梯度下降：梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，因此我们在做梯度下降的时候，应该是沿着梯度的反方向进行权重的更新，可以有效的找到全局的最优解。这个参数的更新过程可以描述为：

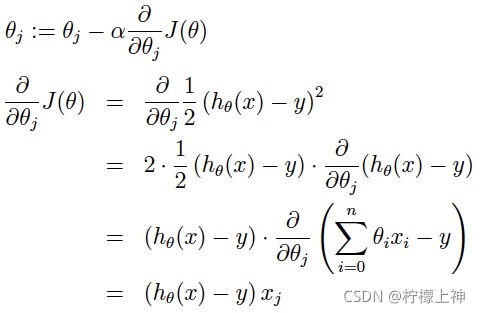
随机梯度下降法

随机梯度下降（SGD）是一种简单但非常有效的方法，多用于支持向量机，逻辑回归（LR）等凸损失函数下的线性分类器的学习。并且SGD已成功应用于文本分类和自然语言处理中经常遇到的大规模和稀疏机器学习问题。

SGD既可以用于分类计算，也可以用于回归计算。

SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。（重点：每次迭代使用一组样本）

为什么叫随机梯度下降算法呢？这里的随机是指每次迭代过程中，样本都要被随机打乱，这个也很容易理解，打乱是有效减小样本之间造成的参数更新抵消问题。

为什么引入SGD?深度神经网络通常有大量的参数需要学习，因此优化算法的效率和精度非常重要。传统的梯度下降算法需要计算全部样本的梯度，非常耗时，并且容易受到噪声的影响。随机梯度下降算法则可以使用一小部分样本来计算梯度，从而大大提高了训练速度和鲁棒性。此外，SGD还可以避免陷入布局最小值，使得训练结果更加准确。

 

对于权值的更新不再通过遍历全部的数据集，而是选择其中的一个样本即可。一般来说其步长的选择比梯度下降法的步长要小一点，因为梯度下降法使用的是准确梯度，所以它可以朝着全局最优解（当问题为凸问题时）较大幅度的迭代下去，但是随机梯度法不行，因为它使用的是近似梯度，或者对于全局来说有时候它走的也许根本不是梯度下降的方法，故而它走的比较缓，同样这样带来的好处就是相比于梯度下降法，它不是那么容易陷入到局部最优解中去。

更新公式：

 

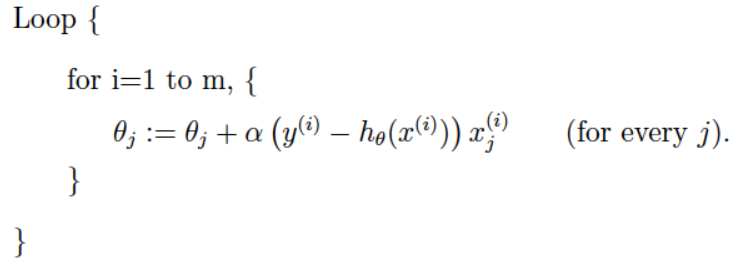
 分类

随机梯度下降算法通常还有三种不同的应用方式，它们分别是SGD,Batch-SGD,Mini-SGD

1.SGD是最基本的随机梯度下降，它是指每次参数更新只使用一个样本，这样可能导致更新较慢。

2.Batch-SGD是批随机梯度下降，它是指每次参数更新使用所有样本，即把所有样本都代入计算一遍，然后取它们的参数更新均值，来对参数进行一次性更新，这种更新方式较为粗糙；

3.Mini-Batch-SGD是小批量随机梯度下降，它是指每次参数更新使用一小批样本，这批样本的数量通常可以采用trial-and-error的方法来确定，这种方法被证明可以有效加快训练速度。

优点：

（1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。

缺点：

（1）准确率下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。

（2）可能会收敛到局部最优，由于单个样本并不能代表全部样本的趋势。

（3）不易于并行实现。

代码：

import torch
from torch import nn
from torch import optim

data = torch.tensor([[0,0],[0,1],[1,0],[1,1.]],requires_grad=True)
target = torch.tensor([[0],[0],[1],[1.]],requires_grad=True)

model = nn.Linear(2,1)

def train():
    opt = optim.SGD(params=model.parameters(),lr = 0.1)
    for iter in range(20):
        # 消除之前的梯度(如果存在)
        opt.zero_grad()
        # 预测
        pred = model(data)
        # 计算损失
        loss = ((pred - target)**2).sum()
        # 指出那些导致损失的参数
        loss.backward()
        for name,param in model.named_parameters():
            print(name,param.data,param.grad)

        #更新参数
        opt.step()
        print(loss.data)

if __name__ == "__main__":
    train()

 optim.SGD()是pytorch中的随机梯度下降优化器，它可以调整神经网络中的参数以最小化损失函数。它是一种梯度下降优化算法，通过迭代每个参数，以最小化损失函数。它的基本思想是，在每次迭代中，每个参数都会沿着梯度的反方向移动一小步，以期望最小化损失函数。

结果：

weight tensor([[0.3631, 0.4273]]) tensor([[0.9060, 3.0344]])
bias tensor([0.6498]) tensor([4.3597])
tensor(1.7762)
weight tensor([[0.2725, 0.1238]]) tensor([[-1.8072, -0.1044]])
bias tensor([0.2138]) tensor([-0.7042])
tensor(0.5756)
weight tensor([[0.4532, 0.1343]]) tensor([[-0.7817,  0.5805]])
bias tensor([0.2842]) tensor([0.6238])
tensor(0.3414)
weight tensor([[0.5314, 0.0762]]) tensor([[-0.8347,  0.2551]])
bias tensor([0.2219]) tensor([0.2053])
tensor(0.2281)
weight tensor([[0.6148, 0.0507]]) tensor([[-0.6339,  0.2379]])
bias tensor([0.2013]) tensor([0.2729])
tensor(0.1556)
weight tensor([[0.6782, 0.0269]]) tensor([[-0.5371,  0.1604]])
bias tensor([0.1740]) tensor([0.2130])
tensor(0.1071)
weight tensor([[0.7319, 0.0109]]) tensor([[-0.4395,  0.1184]])
bias tensor([0.1527]) tensor([0.1933])
tensor(0.0743)
weight tensor([[ 0.7759, -0.0009]]) tensor([[-0.3647,  0.0817]])
bias tensor([0.1334]) tensor([0.1671])
tensor(0.0520)
weight tensor([[ 0.8123, -0.0091]]) tensor([[-0.3020,  0.0551]])
bias tensor([0.1167]) tensor([0.1466])
tensor(0.0366)
weight tensor([[ 0.8425, -0.0146]]) tensor([[-0.2509,  0.0348]])
bias tensor([0.1020]) tensor([0.1281])
tensor(0.0260)
weight tensor([[ 0.8676, -0.0181]]) tensor([[-0.2087,  0.0198]])
bias tensor([0.0892]) tensor([0.1120])
tensor(0.0186)
weight tensor([[ 0.8885, -0.0201]]) tensor([[-0.1740,  0.0088]])
bias tensor([0.0780]) tensor([0.0980])
tensor(0.0134)
weight tensor([[ 0.9059, -0.0210]]) tensor([[-0.1454,  0.0009]])
bias tensor([0.0682]) tensor([0.0857])
tensor(0.0098)
weight tensor([[ 0.9204, -0.0211]]) tensor([[-0.1217, -0.0047]])
bias tensor([0.0597]) tensor([0.0749])
tensor(0.0071)
weight tensor([[ 0.9326, -0.0206]]) tensor([[-0.1020, -0.0084]])
bias tensor([0.0522]) tensor([0.0655])
tensor(0.0052)
weight tensor([[ 0.9428, -0.0197]]) tensor([[-0.0857, -0.0109]])
bias tensor([0.0456]) tensor([0.0573])
tensor(0.0039)
weight tensor([[ 0.9514, -0.0187]]) tensor([[-0.0722, -0.0123]])
bias tensor([0.0399]) tensor([0.0501])
tensor(0.0029)
weight tensor([[ 0.9586, -0.0174]]) tensor([[-0.0609, -0.0130]])
bias tensor([0.0349]) tensor([0.0438])
tensor(0.0021)
weight tensor([[ 0.9647, -0.0161]]) tensor([[-0.0515, -0.0131]])
bias tensor([0.0305]) tensor([0.0383])
tensor(0.0016)
weight tensor([[ 0.9698, -0.0148]]) tensor([[-0.0436, -0.0129]])
bias tensor([0.0267]) tensor([0.0335])
tensor(0.0012)