知识图谱-TransH模型

TransH:将知识嵌入到超平面(Knowledge graph embedding by translating on hyperplanes)

1.从TransE到TransH模型

在之前的文章知识图谱-TransE模型原理中，我们介绍了TransE模型的基本原理，对于TransE模型而言，其核心思想为：h + r = t

其中h时头实体向量，r是关系向量，t是尾实体向量。根据这个核心公式，我们不难发现其存在着一定的局限性。比如当存在多对一关系的时候，假设（h₁,r,t）,(h₂,r,t),根据TransE的假设，可以确定的是：

h₁ + r = t, h₂ + r =t

这使得h₁,h₂两个头实体的向量过于相近。与此同时，当存在（h,r,t）,(t,r,h)均在图谱中出现的时候，会计算出r=0,h=t.

总的来说，TransE模型在处理多对一，多对多，自反关系的时候，会有很多局限性。为了解决上面的我们提到的问题,提出了TransH模型。

2.TransH模型

2.1基本思想

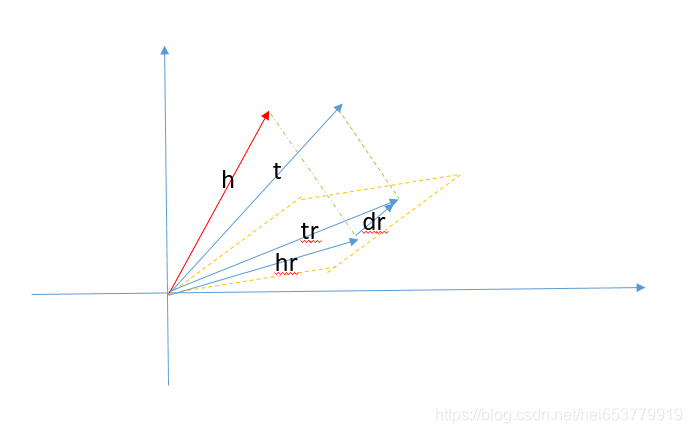
TransH全称是Knowledge Graph Embedding by Translating on Hyperplanes,直译为超平面上的知识图谱词嵌入。针对每一个关系r,都给出一个超平面Wr,在Wr超平面上定义关系向量dr,在将原有的头实体h和尾实体t映射到超平面上为hr,tr。要求正确的三元组满足下面的公式

hr + dr = tr.

我们用一张图来表示这个过程：

 

2.2相对于TransE的改进

我们之前提到了，在TransE模型中，如果h1和h2向量都存在着同一个关系r和同一个尾实体t。那么在TransE中h1和h2是相同的。由于TransE在一对多，多对一，多对多关系时或者自反关系上效果不是很好，所以TransH被提出。

自反关系：指head和tail相同，例如：

（曹操  欣赏   曹操）这是自反关系，（曹操  欣赏  司马懿）这不是自反关系。

一对一：指同一组head,relation只会对应一个tail。例如：

（司马懿  妻子  张春华），（诸葛亮  妻子   黄月英）

一对多：指同一组head，relation会对应多个不同的tail。例如：

（司马懿  小妾  柏灵筠） ，（司马懿   小妾  静姝）

多对一：指多个head会对应同一组relation,tail。例如：

（司马师  父亲  司马懿） ，（司马昭  父亲   司马懿）

多对多：指多组head ,relatioin对应多个tail。例如：

（司马懿  懂得  孙子兵法），（司马懿  懂得  三略），（司马懿   懂得   六韬）

（诸葛亮  懂得   孙子兵法），（诸葛亮  懂得  三略），（诸葛亮   懂得    六韬）

（周公瑾   懂得  孙子兵法），（周公瑾    懂得   三略），（周公瑾   懂得    六韬）

 

为什么TransE会在一对多等关系上效果不好，比如我们看两组关系，（司马懿  小妾  柏灵筠），（司马懿  小妾  静姝）。因为两组关系都存在实体“司马懿”和关系“小妾”，那么如果只简单考虑h + r = t,那么 “柏灵筠” = “司马懿”+“小妾”和“静姝” = “司马懿”+“小妾”，所以“柏灵筠”=“静姝”，很显然，这并不是我们想要的结果。

再比如自反关系，（曹操  欣赏   曹操），“曹操” + “欣赏” = “曹操”，所以“欣赏” = 0.如果你非要说如果存在自反关系，relation就该为0，那么轮到计算（曹操  欣赏   司马懿）时，如果将“欣赏” = 0代入，则会产生“曹操” = “司马懿”的将结果。当然TransE在实际迭代中也不会这样，原因是因为（曹操  欣赏  司马懿）这类的数据大概率会在训练集中占大多数，而（曹操  欣赏  曹操）会被它当作噪音数据一样的存在，所以会影响效果。

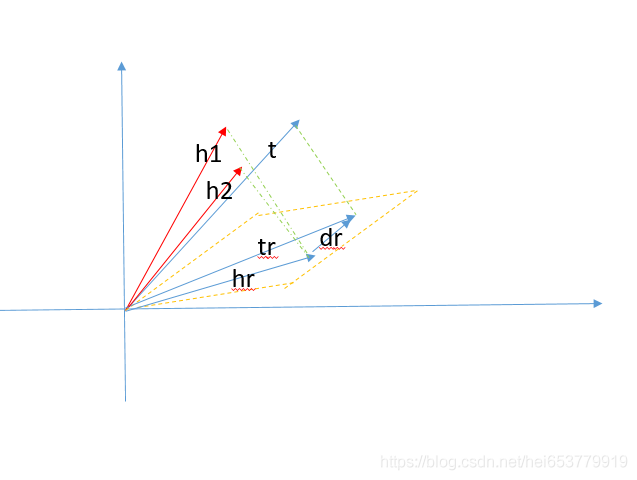
而在TransH中，如果对于h1和h2向量都存在一个三元组(h1,r,t)和（h2,r,t）。通过TransH中关系r的超平面的映射，则有：h_1r+dr = t_r

h_2r+dr = t_r

也就是说h₁,h₂在超平面上的映射是形同或者近似的。但是对于h₁,h₂本身可以是不相近的，也就是可以区分的。如下图所示：

 

2.3TransH数学推导

首先，我们假设w为关系平面Wr的单位法向量，在原始的向量h在法向量w上的投影长度为：

|w|*|h|*cosθ

整理成向量的形式就是：

|w|*|h|*cosθ*w

其中，一定要注意的是w是单位法向量。

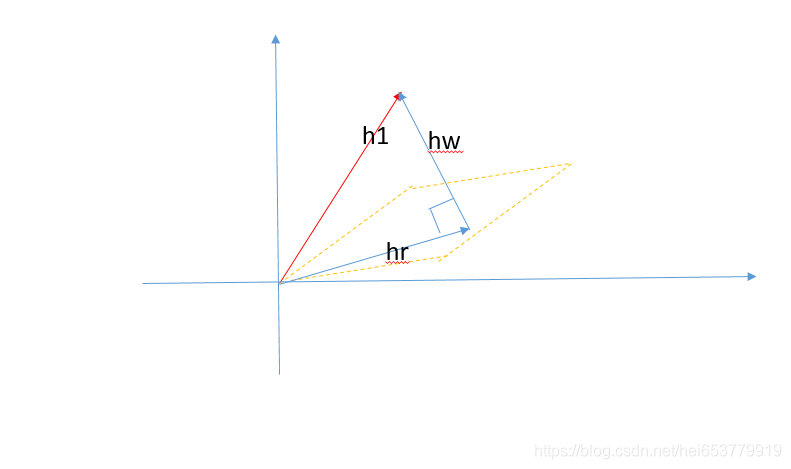
也就是说，原始向量h在关系平面Wr上的单位法向量的投影为：

h_w = w^Thw

我们用图来表示就是：

 

则，我们可以确定的是对于映射向量hr有：

h_r = h - h_w = h - w^Thw

同理，我们可以确定的有：

t_w = w^Ttw

t_r = t-t_w = t-w^Ttw

然后我们回忆一下，TransE模型中目标函数：

 

 

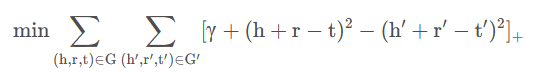
 这里我们采用的是L2范数，在TransH中，我们也采用这种方式，与TransE模型的目标函数类似，我们希望的是最小化在关系平面上的正确三元组的距离差，最小化错误三元组距离差的相反数，也就是：

 

 

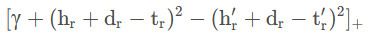
 其中，[x]₊表示max(x,0),而对于 hr​,tr​,hr′​,tr′​有：

h_r = h - h_w = h-w^Thw

t_r = t - t_w = t - w^Ttw

t_r′​ = t' - t_w'=t' - w^Tt'w

h_r' = h'-h_w' = h' - w^Th'w

$$则可以定义总的目标函数为：$$

 

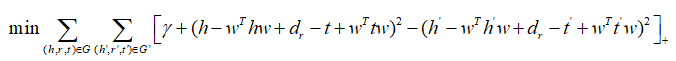
 进而，损失函数就确定为：

 

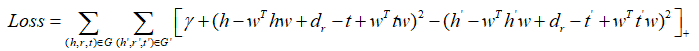
 根据损失函数分别对参数进行求导，同理。

原文链接：https://blog.csdn.net/hei653779919/article/details/104296370