Pytorch中norm(几种范数norm的详细介绍)
1.范数（norm）的简单介绍
概念：
距离的定义是一个宽泛的概念，只要满足非负，自反，三角不等式就可以称之为距离。范数是一种强化了的距离概念，它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解，我们可以把范数当作距离来理解。
在数学上，范数包括向量范数和矩阵范数，向量范数表征向量空间中向量的大小，矩阵范数表征矩阵引起变化的大小。
一种非严密的解释就是，对应向量范数，向量空间中的向量都是有大小的，这个大小如何度量，就是用范数来度量的，不同的范数都可以来度量这个大小；对于矩阵范数，学过线性代数，通过运算AX = B ,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
1.1 L-P范数
与闵可夫斯基距离的定义一样，L-P范数不是一个范数，而是一组范数，其定义如下：
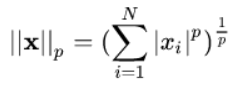
根据P的变化，范数也有着不同的变化，一个经典的有关P范数的变化图如下：
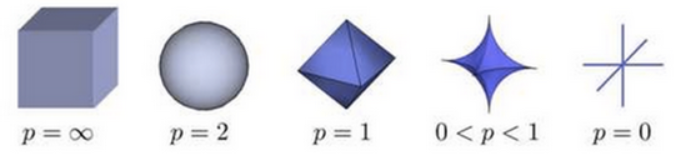
上图表示了p从无穷到0变化时，三维空间中到原点的距离(范数)为1的点构成的图形的变化情况。以常见的L-2范数
（p=2）为例，此时的范数也即欧式距离，空间中到原点的欧式距离为1的点构成了一个球面。
1.2 L0范数
当P=0时，也就是L0范数，由上面可以，L0范数并不是一个真正的范数，它主要被用来度量向量中非零元素的个数。
1.3 L1范数
L1范数是我们经常见到的一种范数，它的定义如下：
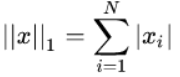
表示向量x中非零元素的绝对值之和。
L1范数有很多的名字，例如我们熟悉的曼哈顿距离，最小绝对误差等。使用L1范数可以度量两个向量间的差异，如绝对误差和。
1.4 L2范数
L2范数是我们最常见最常用的范数了，我们用的最多的度量距离欧式距离就是一种L2范数，它的定义如下：
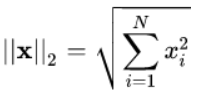
Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开放，pytorch调用函数norm(x,2)。
像L1范数一样，L2也可以度量两个向量间的差异，如平方差和：SSD
L2范数通常会被用来做优化函数的正则化项，防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。
1.5 无穷范数
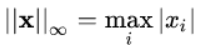
即所有向量元素绝对值中的最小值，matlab调用函数norm(x,-inf)
2.矩阵范数
2.1 1-范数
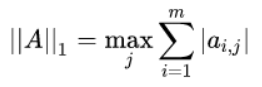
列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A，1)
2.2 2-范数
对于实矩阵A,它的谱范数定义为：
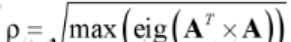
其中，eig(X)为计算方阵X特征值，它返回特征值向量：谱范数，即A'A矩阵的最大特征值的开平方。matlab调用函数norm(x,2)。
2.3 无穷范数
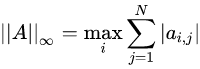
行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A,inf)。
2.4 F-范数
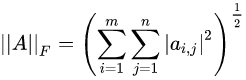
Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A,'fro')
2.6核范数
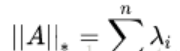
是A的奇异值，核范数即奇异值之和。
3.Pytorch中的x.norm(p=2,dim=1,keepdim=True)的理解
3.1 方法介绍
代码：x.norm(p=2,dim=1,keepdim=True)
功能：求指定维度上的范数
函数原型：返回输入张量给定维dim上每行的p范数
torch.norm(input,p,dim,out=None,keepdim=False) ->Tensor
注：范数求法：对N个数据求p范数
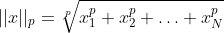
3.2函数参数
input(Tensor) -输入张量
p(float) - 范数计算中的幂指数值
dim(int) - 缩减的维度，dim=0是对0维度上的一个向量求范数，返回结果数量等于其列的个数，也就是说有多少个0维度的向量，将得到多少个范数.dim=1同理。
out(Tensor,optional) - 结果张量
keepdim(bool) - 保持输出的维度。当keepdim = False时，输出比输入少一个维度（就是指定的dim求范数的维度）。而keepdim = True时，输出与输入维度相同，仅仅时输出在求范数的维度上元素个数变为1。这也是为什么有时我们把参数中的dim称为缩减的维度，因为norm运算之后，此维度或者消失或者元素个数变为1.
3.3实例演示
import torch import numpy as np data = torch.tensor([ [1., 2., 3., 4.], [ 2., 4., 6., 8.], [ 3., 6., 9., 12.] ]) print(torch.norm(data,p=2,dim=1,keepdim=True) )#按行
输出：
tensor([[ 5.4772], [10.9545], [16.4317]])
print(torch.norm(data,p=2,dim=0,keepdim=True) ) #按列
输出
tensor([[ 3.7417, 7.4833, 11.2250, 14.9666]])
3.2.2 keepdim参数
print(torch.norm(data,p=2,dim=1)) print(torch.norm(data,p=2,dim=1,keepdim=False))
输出：
tensor([ 5.4772, 10.9545, 16.4317])
tensor([ 5.4772, 10.9545, 16.4317])
可以看到输出少了一维，其实就是dim=1(求范数)那一维（列）少了，因为从4列变成1列，就是三行中求每一行的2范数，就剩下1列了，不保持这一维不会对数据产生影响。或者也可以这么理解，就是数据中每个数据有没有用[]扩起来。
不写keepdim，则默认不保留dim的那个维度
不写dim,则计算Tensor中所有元素的2范数
print(torch.norm(data,p=2))
输出
tensor(20.4939)
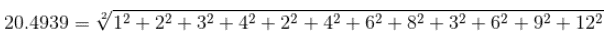
与上面一样的效果，默认是L2范数
torch.norm(data)
输出
tensor(20.4939)
首先，它对张量y每个元素进行平方，然后对它们求和，最后取平方根。
原文：https://blog.csdn.net/qq_46092061/article/details/121498557
