2020牛客暑期多校训练营（第二场）F二维单调队列

 

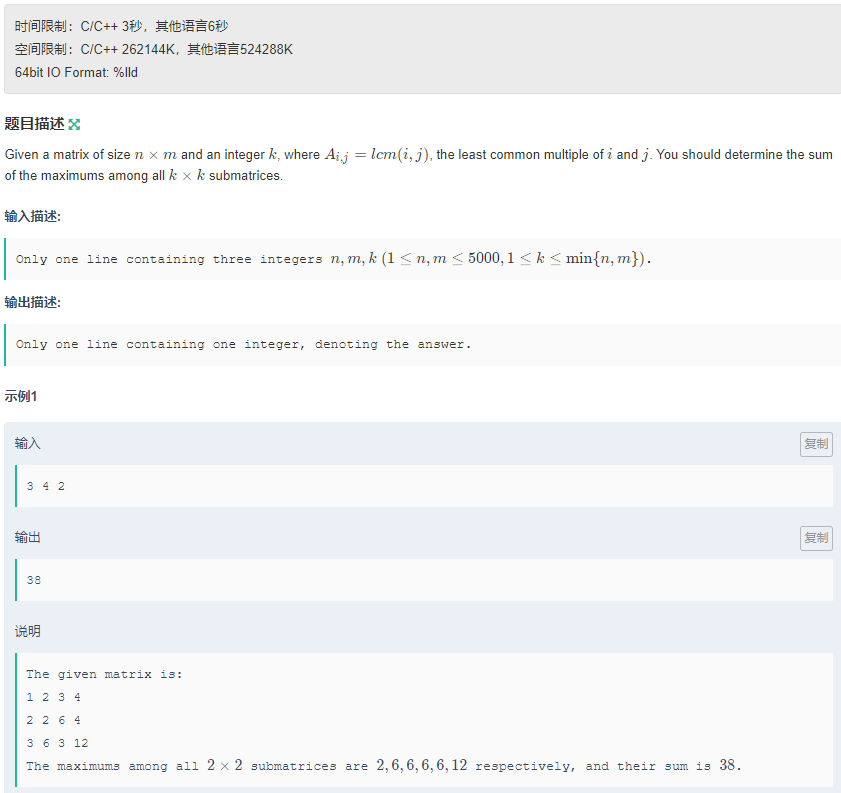
 本题所用到的算法：二维单调队列

一维单调队列：

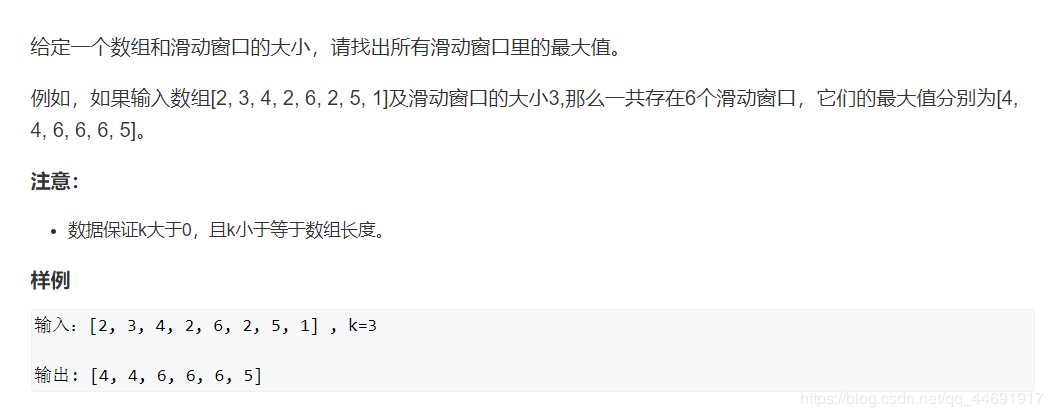
 首先不难分析窗口是这样滑动的：

 

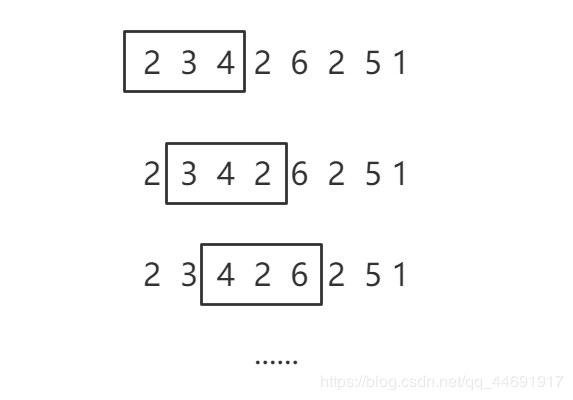
如果我们使用尺取/滑动窗口，时间复杂度为O(n*k)，当k很大时容易超时。本题采用单调队列优化

所谓单调队列即双端队列，队列中的值是单调的，在每次滑动之后维持队列的单调性

对于本题来说，每次都是最左端的数移除队列，最右边的数加入队列，由于队列的单调性我们直接取队列的最左端的值，即为区间最值

对于此题来说需要降序的单调队列：

对于新加入的数，我们需要判断前面是否都是比它大的。因为如果它更大，区间在移动过程中（实际是该数慢慢左移直到移出队列过程中），前面的数不可能作为最大值，所以我们需要降序维持队列单调性

 

队列中直接存每个数吗？

• 一开始我也是这么想的，但是写着写着发现无法实现，如果我们存数的话我们需要知道当前队列的长度是否超过k。但是区间长度是变化的，一般小于k，因此没有办法动态维护

• 因此我们存每个数的下标去操作，具体看下面的常规代码

常规代码：

#include <set>
#include <map>
#include <stack>
#include <queue>
#include<iostream>
using namespace std;
#define lowbit(x) (x&(-x))
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> P;
const double eps=1e-8;
const int inf=0x3f3f3f3f;
const ll INF=1e18;
const int Mod=1e9+7;
const int maxn=2e5+10;

int q[maxn],a[maxn];  //数组维护双端队列即可

int main(){
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>a[i];
    int l=1,r=1;
    for(int i=1;i<=n;i++){   //注意边界的判断
        while(r-l>0 && q[l]<=i-k) 
            l++;  //将前面超过长度k的删除
        while(r-l>0 && a[q[r-1]]<=a[i])
            r--;  //将小于这个下标值删除，注意这里是a[q[r-1]]
        q[r++]=i;  //每次添加当前下标
        if(i>=k) 
            cout<<a[q[l]]<<" "; //只有长度达到k之后才能输出区间最值
    }
    return 0;
}
//8 3
//2 3 4 2 6 2 5 1

本题：

思路：

    考虑 一维 求每一行每k 个元素的最大值 ，很容易想到单调队列（滑动窗口），可以维护每个长度为 k 的区间的最大值，但这里是二维的，其实只要在一维的基础上 再对列做单调队列。因为在一维单调队列的基础上，我们已经求得了第 i 行 第 j个元素为起点长度为 k 的区间的最大值 ，在求整个区间时就只要用我们已经得到的值来求就好了。

#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long ll;
const int maxn = 5e3+5;
int a[maxn][maxn],ans[maxn][maxn],que[maxn];
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}
int lcm(int a,int b){
    return a*b/gcd(a,b);
}

int main(){
    int n,m,k;
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            a[i][j]=lcm(i,j);
        }
    }
    for(int i=1;i<=n;i++){
        int head=1,tail=1;
        for(int j=1;j<=m;j++){
            while(tail-head>0&&que[head]<=j-k) head++;
            while(tail-head>0&&a[i][que[tail-1]]<=a[i][j]) tail--;
            que[tail++]=j;
            ans[i][j] = a[i][que[head]];
//            cout<<ans[i][j]<<endl;
        }
    }
    for(int j=1;j<=m;j++){
        int head=1,tail=1;
        for(int i=1;i<=n;i++){
            while(tail-head>0&&que[head]<=i-k) head++;
            while(tail-head>0&&ans[que[tail-1]][j]<=ans[i][j]) tail--;
            que[tail++] =i;
            ans[i][j] = ans[que[head]][j];
//            cout<<ans[i][j]<<endl;
        }
    }
    ll anss=0;
    for(int i=k;i<=n;i++){
        for(int j=k;j<=m;j++){
            anss+=ans[i][j];
//            cout<<ans[i][j]<<" ";
        }
//        cout<<endl;
    }
    cout<<anss<<endl;
    return 0;
}