逆元

1.概念

求（a/b)%m时，因b可能会过大，会出现爆精度的情况，所以需变除法为乘法。若a*x≡1(mod b),且a与b互质，我们定义x是a的逆元，记为a^(-1)或inv(a)。

2.三种方法

2.1 费马小定理

#include<cstdio>
#include<cstring>
using namespace std;
int Quick_Power(int a,int b,int c)
{
    int ans=1;
    while(b)
    {
        if(b&1)
          ans=(1ll*ans*a)%c;
        a=(1ll*a*a)%c;
        b>>=1;
    }
    return ans;
}
int main()
{
    int a,b,p;
    scanf("%d%d%d",&a,&b,&p);
    b=Quick_Power(b,p-2,p);
    printf("%d",((a%p)*(b%p))%p);
    return 0;
}

 

2.2扩展欧几里得

扩展欧几里德算法是用来在已知a, b求解一组x，y，使它们满足贝祖等式： ax+by = gcd(a, b) =d（解一定存在，根据数论中的相关定理）。扩展欧几里德常用在求解模线性方程及方程组中。


算法证明：

a和m是互质的

代码：

#include<cstdio>
#include<cstring>
void exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return;
    }
    exgcd(b,a%b,y,x);
    y-=a/b*x;
}
int main()
{
    int a,b,p,x,y;
    scanf("%d%d%d",&a,&b,&p);
    exgcd(b,p,x,y);
    x=(x+p)%p;
    printf("%d",((a%p)*(x%p))%p);
    return 0;
}

 

2.3 线性筛

就是通过递推求 1 到 n 之间所有数的逆元。

时间复杂度O（）

设x的逆元为x^(-1)

我们先有一个1的逆元为1

设p=k*i+r,(1<r<i<p) 也就是 k 是 p / i的商，r是余数 。

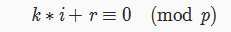
然后乘上i的逆元和r的逆元

然后公式就出来了

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,p;
ll inv[3000005];
int main()
{
    cin>>n>>p;
     inv[1]=1;
     printf("%lld\n",inv[1]);
     for(int i=2;i<=n;i++)
    {
        inv[i]=(p-p/i)*inv[p%i]%p;
         printf("%lld\n",inv[i]);
    }
}