尺取法

顾名思义，像尺子一样取一段，尺取法通常是对数组保存一对下标，即所选取的区间的左右端点，然后根据实际情况不断地推进区间左右端点以得出答案。之所以需要掌握这个技巧，是因为尺取法比直接暴力枚举区间效率高很多，尤其是数据量大的时候，所以尺取法是一种高效的枚举区间的方法，一般用于求取有一定限制的区间个数或最短的区间等等。当然任何技巧都存在其不足的地方，有些情况下尺取法不可行，无法得出正确答案。

也可以说是，在给的一组数据中找到不大于某一个上限的“最优连续子序列”。

尺取法查找大于10的思路如下图，黄色区域是每次查找的区间，第一次先找出左右端点后，固定右端点移动左端点，依次移动左端点直到无法满足的情况下更新右端点。每次比较序列长度得到最优解。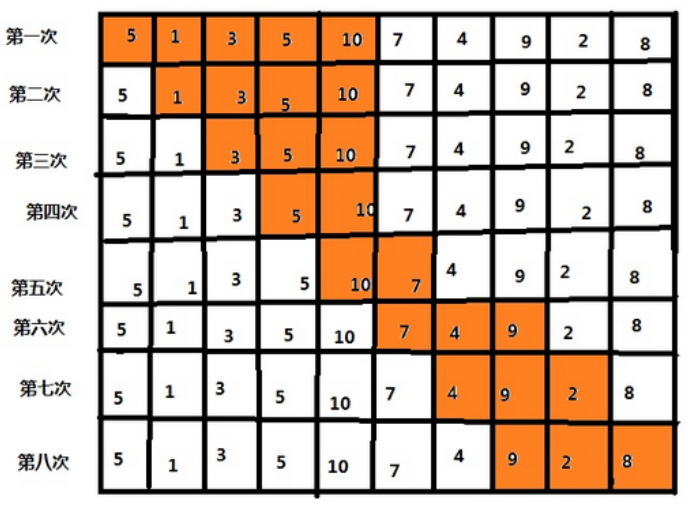

例题一

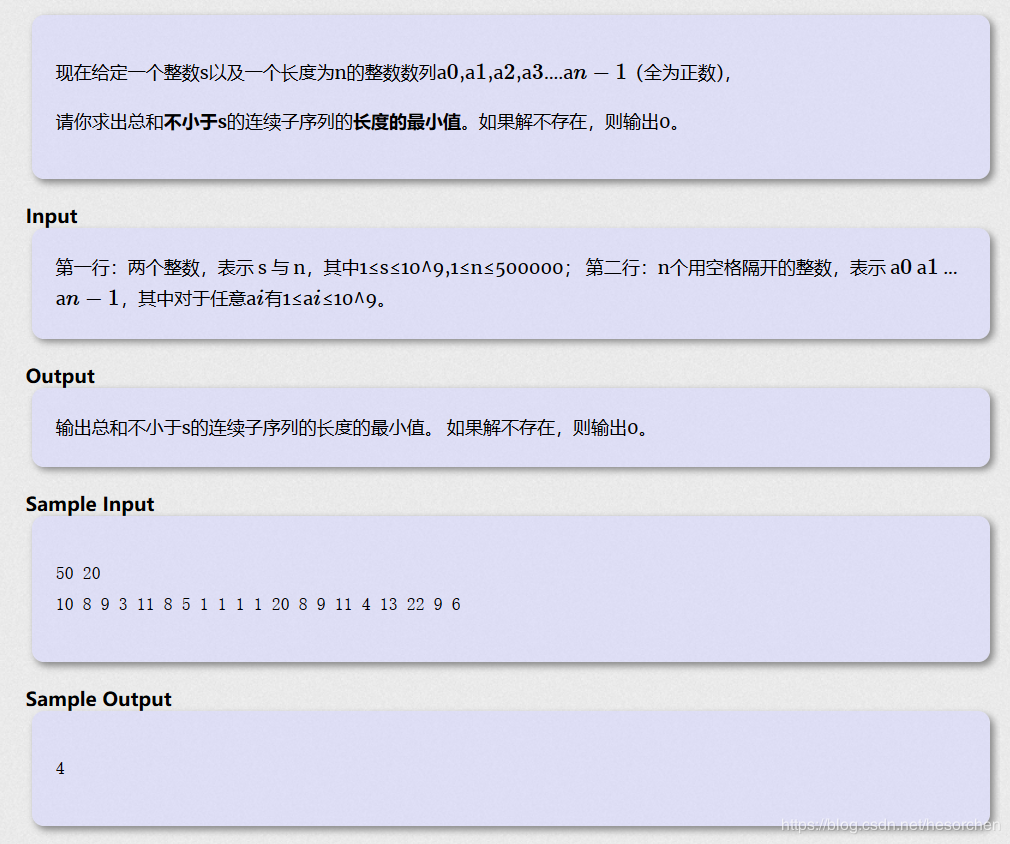
代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll p[500005];
int main()
{
    ll s, n;
    cin >> s >> n;
    ll sum = 0;
    for (int i = 0; i < n; i++)
        cin >> p[i], sum += p[i];
    if (sum < s)
        printf("0\n");
    else
    {
        sum = 0;
        int l = 0, r = 0;
        int ans = n;
        while (1)
        {
            while (r < n && sum < s) //每次将右端点r推到首次满足题意的位置
                sum += p[r++];
            if (sum < s) //如果已经没有满足题意的右端点（即右端点推到尽头）
                break;
            ans = min(ans, r - l); //过程中不断更新答案
            sum -= p[l++];         //左端点向右推动一个单位
        }
        cout << ans << endl;
    }
    return 0;
}

 

例题二

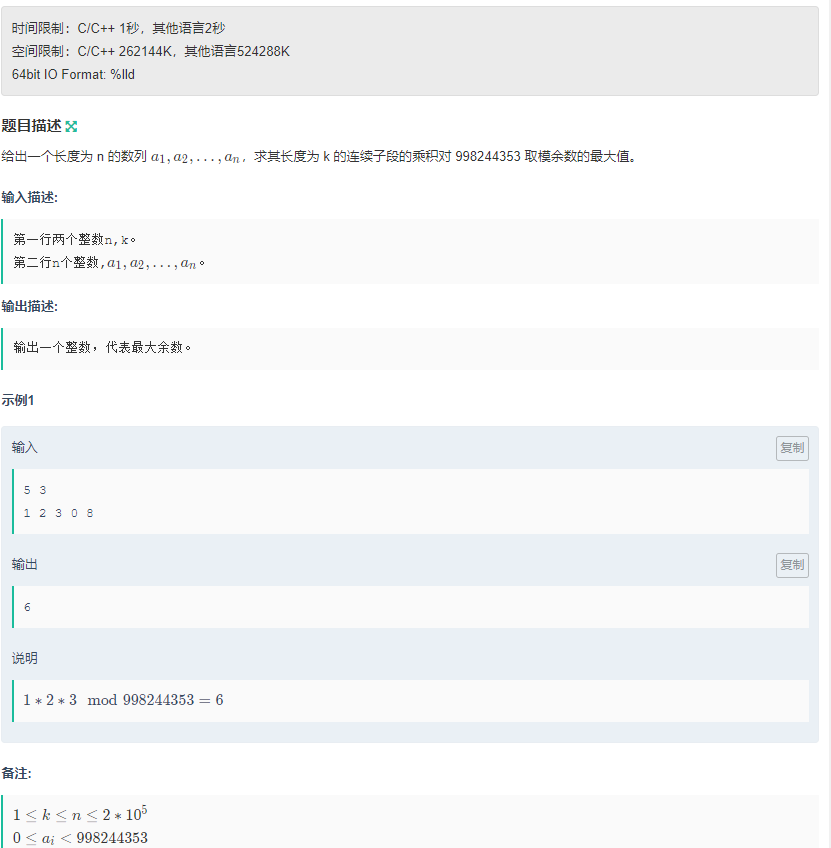
代码：

#include<iostream>
using namespace std;
const int mod = 998244353;
const int maxn = 2e5+10;
typedef long long ll;
ll a[maxn];
ll ans;
ll Power(ll x,ll y){
    ll res =1;
    while(y){
        if(y&1) res=res*x%mod;
        x=x*x%mod;
        y>>=1;
    }
    return res;
}
int main(){
    ll n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++)   
        scanf("%lld",&a[i]);
    ll temp = 1;
    for(int l=1,r=1;r<=n;r++){
        if(!a[r]){
            temp=1,l=r+1;
            continue;
        }
        temp =temp*a[r]%mod;
        while(r-l+1>k){
            temp =temp*Power(a[l],mod-2)%mod;
            l++;
        }
        if(r-l+1==k) ans = max(ans,temp);
    }
    cout<<ans<<endl;
    return 0;
}