牛客练习赛53 B 美味果冻

链接：https://ac.nowcoder.com/acm/contest/1114/B
来源：牛客

时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 524288K，其他语言1048576K
64bit IO Format: %lld

题目描述

 由于n越大jelly越美味，这里n<=3000000,只需求这个式子对1e9+7取模的值。

输入描述:

第一行输入一个整数 n。 1<=n<=3000000。

输出描述:

输出一个整数表示答案。

示例1

输入

复制

3

输出

复制

22

思路：
这道题主要是开始对这个式子的转化过程，这是比较难想的，可能我们就会直接用这个公式去做，这样就会很难做
转化过程：

转化为

 

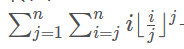
原因：为什么想到去转化，如果不转化的话，那么i/j中j作为分母，并且还有j次幂，而j又在内循环里面，所以很不方便写程序，最理想的是j是外循环里的变量，

接下来，我们来分析为什么是这样转化

对于i=1i=1，有j=1j=1
对于i=2i=2，有　　j=1,2
。。。
对于i=ni=n，有　　j = 1,2,...,n

我们发现i都是大于等于j的，于是就可以得到这个转化的式子

代码：

#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long ll;
const int maxn = 3e6+10;
const ll mod = 1e9+7;
ll a[maxn];
ll div2 = 5e8+4;//2对于1e9+7的逆元
void init1(int k){
    for(int i=1;i<=k;i++)
        a[i] = 1;
} 

void init2(int k){
    for(int i=1;i<=k;i++){
        a[i] = (a[i]*i)%mod;
    }
}

ll f(ll n){
    ll sum = 0;
    init1(n);
    for(ll j = 1 ; j<=n;j++){
        init2(n/j);
        for(ll k = 1;k<=n/j;k++){
            ll mm = min(n,(k+1)*j-1);
            sum = (sum+((((mm-k*j+1+mod)%mod)*(k*j+mm)%mod)*div2%mod)*a[k]%mod)%mod;
            
        }
    }
    return sum%mod;
}
int main(){
    int n;
    cin>>n;
    cout<<f(n)<<endl;
    return 0;
}