代码随想录算法训练营day37 | leetcode 738. 单调递增的数字、968. 监控二叉树
题目链接:738. 单调递增的数字-中等
题目描述:
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10
输出: 9
示例 2:
输入: n = 1234
输出: 1234
示例 3:
输入: n = 332
输出: 299
提示:
0 <= n <= 10^9
此题需要从后往前遍历,当遇到前一位比该位大的时候,将前一位数字减一,向前继续遍历,直到最大位(即第1位),记录下需要改的最大位(即循环里后面遍历到的),从这一位开始后面的都修改为9,得到的就是结果。
代码如下:
// 时间复杂度:O(n),n 为数字长度
// 空间复杂度:O(n),需要一个字符串,转化为字符串操作更方便
class Solution {
public:
int monotoneIncreasingDigits(int n) {
string str = to_string(n);
int flag = str.size();
for (int i = str.size() - 1; i > 0; --i) {
if (str[i - 1] > str[i]) {
--str[i - 1];
flag = i;
}
}
for (int i = flag; i < str.size(); ++i) {
str[i] = '9';
}
return stoi(str);
}
};
题目链接:968. 监控二叉树-困难
题目描述:
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
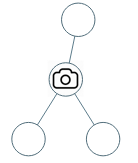
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
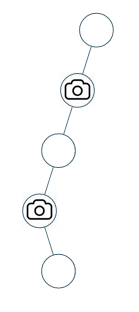
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
主要有如下四类情况:
- 情况1:左右节点都有覆盖
左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。
- 情况2:左右节点至少有一个无覆盖的情况
如果是以下情况,则中间节点(父节点)应该放摄像头
- 情况3:左右节点至少有一个有摄像头
如果是以下情况,其实就是 左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态)
- 情况4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况
代码如下:
// 时间复杂度: O(n),需要遍历二叉树上的每个节点
// 空间复杂度: O(n)
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
// 空节点,该节点有覆盖
if (cur == NULL) return 2;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
// 情况1
// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;
// 情况2
// left == 0 && right == 0 左右节点无覆盖
// left == 1 && right == 0 左节点有摄像头,右节点无覆盖
// left == 0 && right == 1 左节点有无覆盖,右节点摄像头
// left == 0 && right == 2 左节点无覆盖,右节点覆盖
// left == 2 && right == 0 左节点覆盖,右节点无覆盖
if (left == 0 || right == 0) {
result++;
return 1;
}
// 情况3
// left == 1 && right == 2 左节点有摄像头,右节点有覆盖
// left == 2 && right == 1 左节点有覆盖,右节点有摄像头
// left == 1 && right == 1 左右节点都有摄像头
// 其他情况前段代码均已覆盖
if (left == 1 || right == 1) return 2;
// 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解
// 这个 return -1 逻辑不会走到这里。
return -1;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
// 情况4
if (traversal(root) == 0) { // root 无覆盖
result++;
}
return result;
}
};
精简如下:
class Solution {
private:
int result;
int traversal(TreeNode* cur) {
if (cur == NULL) return 2;
int left = traversal(cur->left); // 左
int right = traversal(cur->right); // 右
if (left == 2 && right == 2) return 0;
else if (left == 0 || right == 0) {
result++;
return 1;
} else return 2;
}
public:
int minCameraCover(TreeNode* root) {
result = 0;
if (traversal(root) == 0) { // root 无覆盖
result++;
}
return result;
}
};



