代码随想录算法训练营day34 | leetcode 1005. K 次取反后最大化的数组和、134. 加油站、135. 分发糖果
题目链接:1005. K 次取反后最大化的数组和-简单
题目描述:
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标
i并将nums[i]替换为-nums[i]。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1
输出:5
解释:选择下标 1 ,nums 变为 [4,-2,3] 。
示例 2:
输入:nums = [3,-1,0,2], k = 3
输出:6
解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。
示例 3:
输入:nums = [2,-3,-1,5,-4], k = 2
输出:13
解释:选择下标 (1, 4) ,nums 变为 [2,3,-1,5,4] 。
提示:
1 <= nums.length <= 10^4-100 <= nums[i] <= 1001 <= k <= 10^4
本题的解题步骤为:
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时k--
- 第三步:如果k还大于0,那么反复转变数值最小的元素,将k用完
- 第四步:求和
代码如下:
// 时间复杂度: O(nlogn)
// 空间复杂度: O(1)
class Solution {
static bool cmp(int a, int b) { return abs(a) > abs(b); }
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
sort(nums.begin(), nums.end(), cmp);
int res = 0;
for (int i = 0; i < nums.size(); ++i) {
if (k <= 0)
break;
if (nums[i] < 0 && k > 0) {
--k;
nums[i] *= (-1);
}
}
if (k % 2)
nums[nums.size() - 1] *= (-1);
for (int i = 0; i < nums.size(); ++i) {
res += nums[i];
}
return res;
}
};
题目链接:134. 加油站-中等
题目描述:
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
gas.length == ncost.length == n1 <= n <= 10^50 <= gas[i], cost[i] <= 10^4
本题暴力思路为两层循环,遍历每个起点,从该起点出发,尝试能否跑完所有站点,若找到则返回。for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,要善于使用while!
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
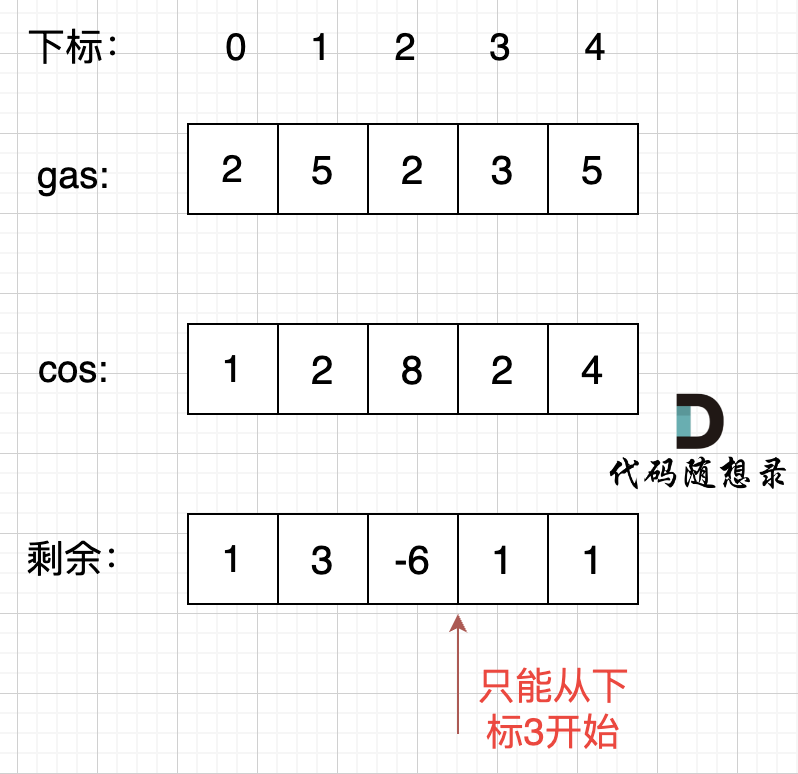
代码如下:
// 时间复杂度: O(n)
// 空间复杂度: O(1)
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int sum = 0; // 总剩余油量
int cur = 0; // 当前起始位置
int curSum = 0; // 从当前起始位置出发后目前的总油量
for (int i = 0; i < gas.size(); ++i) {
int rest = gas[i] - cost[i];
curSum += rest;
sum += rest;
if (curSum < 0) {
cur = i + 1;
curSum = 0;
}
}
if (sum < 0)
return -1;
return cur;
}
};
题目链接:135. 分发糖果-困难
题目描述:
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
提示:
n == ratings.length1 <= n <= 2 * 10^40 <= ratings[i] <= 2 * 10^4
这道题目一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
代码如下:
// 时间复杂度: O(n)
// 空间复杂度: O(n)
class Solution {
public:
int candy(vector<int>& ratings) {
vector<int> candys(ratings.size(), 1);
for (int i = 1; i < ratings.size(); ++i) {
if (ratings[i] > ratings[i - 1])
candys[i] = candys[i - 1] + 1;
}
for (int i = ratings.size() - 2; i >= 0; --i) {
if (ratings[i] > ratings[i + 1])
candys[i] = max(candys[i], candys[i + 1] + 1);
}
int res = 0;
for (int a : candys)
res += a;
return res;
}
};



