代码随想录算法训练营day20 | leetcode 654. 最大二叉树、617. 合并二叉树、700. 二叉搜索树中的搜索、98. 验证二叉搜索树
题目链接：654. 最大二叉树-中等
题目描述：
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点，其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 *最大二叉树* 。
示例 1：
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
- 空数组，无子节点。
- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
- 空数组，无子节点。
- 只有一个元素，所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
- 只有一个元素，所以子节点是一个值为 0 的节点。
- 空数组，无子节点。
示例 2：
输入：nums = [3,2,1]
输出：[3,null,2,null,1]
提示：
1 <= nums.length <= 10000 <= nums[i] <= 1000nums中的所有整数 互不相同
可以将其优化，就是每次分隔不用定义新的数组，而是通过下标索引直接在原数组上操作。
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
if (nums.size() == 0)
return NULL;
int rootIndex = max_element(nums.begin(), nums.end()) - nums.begin();
TreeNode* root = new TreeNode(nums[rootIndex]);
if (nums.size() == 1)
return root;
vector<int> leftNums(nums.begin(), nums.begin() + rootIndex);
vector<int> rightNums(nums.begin() + rootIndex + 1, nums.end());
/* 也可以替换为
// nums.erase(nums.begin() + rootIndex);
// vector<int> rightNums(nums.begin() + rootIndex, nums.end());
*/
root->left = constructMaximumBinaryTree(leftNums);
root->right = constructMaximumBinaryTree(rightNums);
return root;
}
};
题目链接：617. 合并二叉树-简单
题目描述：
给你两棵二叉树： root1 和 root2 。
想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1：
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]
示例 2：
输入：root1 = [1], root2 = [1,2]
输出：[2,2]
提示：
- 两棵树中的节点数目在范围
[0, 2000]内 -10^4 <= Node.val <= 10^4
也可以定义一棵新的树
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if (root1 == NULL)
return root2;
else if (root2 == NULL)
return root1;
else
root1->val += root2->val;
root1->left = mergeTrees(root1->left, root2->left);
root1->right = mergeTrees(root1->right, root2->right);
return root1;
}
};
题目链接：700. 二叉搜索树中的搜索-简单
题目描述：
给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。
示例 1:
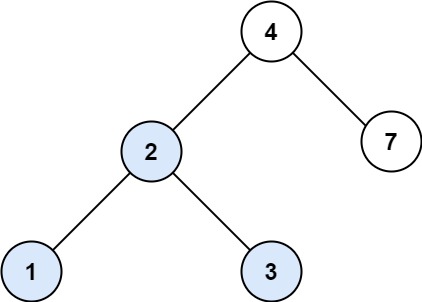
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]
示例 2:
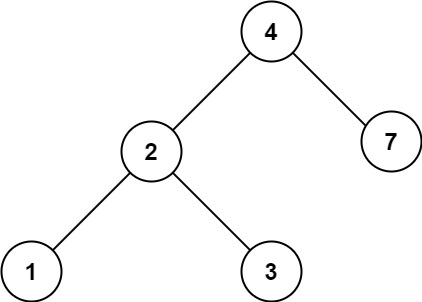
输入：root = [4,2,7,1,3], val = 5
输出：[]
提示：
- 树中节点数在
[1, 5000]范围内 1 <= Node.val <= 10^7root是二叉搜索树1 <= val <= 10^7
用迭代法将更加简单
代码如下：
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
if(root == NULL) return NULL;
if(val < root->val)
return searchBST(root->left, val);
if(val > root->val)
return searchBST(root->right, val);
return root;
}
};
题目链接：98. 验证二叉搜索树-中等
题目描述：
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
-
节点的左
子树
只包含
小于
当前节点的数。
-
节点的右子树只包含 大于 当前节点的数。
-
所有左子树和右子树自身必须也是二叉搜索树。
示例 1：
输入：root = [2,1,3]
输出：true
示例 2：
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。
提示：
- 树中节点数目范围在
[1, 10^4]内 -23^1 <= Node.val <= 23^1 - 1
陷阱：可能会采用后序遍历，如果左右子树都为二叉树则将结果返回给父节点，这样容易造成左子树中的右节点比父节点大，右子树同理。因此需要采取中序遍历
代码如下：
class Solution {
public:
TreeNode* pre = NULL;
bool isValidBST(TreeNode* root) {
if(root == NULL) return true;
bool leftTree = isValidBST(root->left);
if(pre != NULL && pre->val >= root->val)
return false;
pre = root;
bool rightTree = isValidBST(root->right);
return leftTree && rightTree;
}
};
