代码随想录算法训练营day17 | leetcode 110. 平衡二叉树、257. 二叉树的所有路径、404. 左叶子之和
题目链接:110. 平衡二叉树-简单
题目描述:
给定一个二叉树,判断它是否是平衡二叉树
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -10^4 <= Node.val <= 10^4
重点:
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
代码可精简
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
int getHeight(TreeNode* root) {
if (root == NULL)
return 0;
int lHeight = getHeight(root->left);
if (lHeight == -1)
return -1;
int rHeight = getHeight(root->right);
if (rHeight == -1)
return -1;
if (abs(lHeight - rHeight) > 1)
return -1;
return max(lHeight, rHeight) + 1;
}
bool isBalanced(TreeNode* root) {
int res = getHeight(root);
return res == -1 ? false : true;
}
};
题目链接:257. 二叉树的所有路径-简单
题目描述:
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
迭代法:
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
if (root == NULL)
return res;
stack<TreeNode*> stTree;
stack<string> stPath;
stTree.push(root);
stPath.push(to_string(root->val));
while (!stTree.empty()) {
TreeNode* cur = stTree.top();
stTree.pop();
string path = stPath.top();
stPath.pop();
if (cur->left == NULL && cur->right == NULL) {
res.push_back(path);
}
if (cur->left) {
stTree.push(cur->left);
stPath.push(path + "->" + to_string(cur->left->val));
}
if (cur->right) {
stTree.push(cur->right);
stPath.push(path + "->" + to_string(cur->right->val));
}
}
return res;
}
};
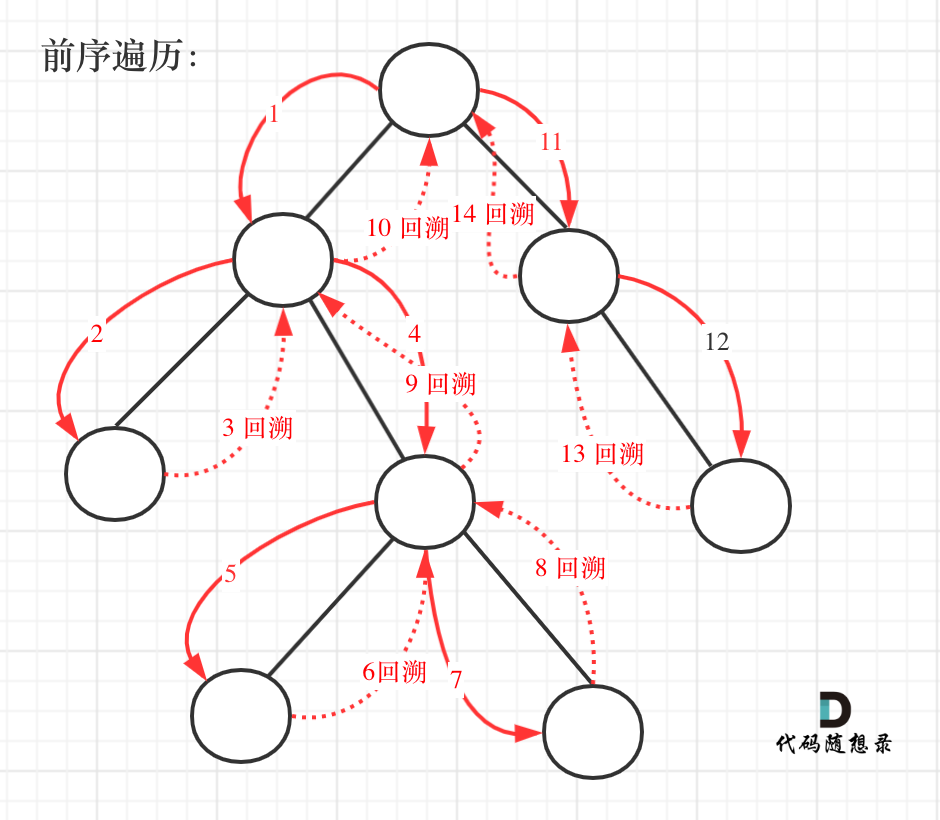
递归法:
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void traversal(TreeNode* root, vector<int>& ndoeVal, vector<string>& res) {
ndoeVal.push_back(root->val);
if (root->left == NULL && root->right == NULL) {
string sPath;
for (int i = 0; i < ndoeVal.size() - 1; ++i) {
sPath += to_string(ndoeVal[i]);
sPath += "->";
}
sPath += to_string(ndoeVal[ndoeVal.size() - 1]);
res.push_back(sPath);
return;
}
if (root->left){
traversal(root->left, ndoeVal, res);
ndoeVal.pop_back(); // 将叶子节点弹出
}
if (root->right){
traversal(root->right, ndoeVal, res);
ndoeVal.pop_back(); // 将叶子节点弹出
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> res;
vector<int> ndoeVal;
traversal(root, ndoeVal,res);
return res;
}
};
题目链接:404. 左叶子之和-简单
题目描述:
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 0;
int lSum = sumOfLeftLeaves(root->left);
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL)
lSum = root->left->val;
int rSum = sumOfLeftLeaves(root->right);
return lSum + rSum;
}
};



