代码随想录算法训练营day15 | leetcode 【二叉树的层序遍历十题】、226. 翻转二叉树、101. 对称二叉树、100. 相同的树、572. 另一棵树的子树
目录
- 题目链接：102. 二叉树的层序遍历-中等
- 题目链接：107. 二叉树的层序遍历 II-中等
- 题目链接：199. 二叉树的右视图-中等
- 题目链接：637. 二叉树的层平均值-简单
- 题目链接：429. N 叉树的层序遍历-中等
- 题目链接：515. 在每个树行中找最大值-中等
- 题目链接：116. 填充每个节点的下一个右侧节点指针-中等
- 题目链接：117. 填充每个节点的下一个右侧节点指针 II-中等
- 题目链接：104. 二叉树的最大深度-简单
- 题目链接：111. 二叉树的最小深度-简单
- 题目链接：226. 翻转二叉树-简单
- 题目链接：101. 对称二叉树-简单
- 题目链接：100. 相同的树-简单
- 题目链接：572. 另一棵树的子树-简单
题目链接：102. 二叉树的层序遍历-中等
题目描述：
给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。
示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]
示例 2：
输入：root = [1]
输出：[[1]]
示例 3：
输入：root = []
输出：[]
提示：
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。而这种层序遍历方式就是图论中的广度优先遍历
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
TreeNode* cur;
while(!que.empty()){
int size = que.size();
vector<int> subRes;
while(size--){
cur = que.front();
que.pop();
subRes.push_back(cur->val);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
res.push_back(subRes);
}
return res;
}
};
题目链接：107. 二叉树的层序遍历 II-中等
题目描述：
给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]
示例 2：
输入：root = [1]
输出：[[1]]
示例 3：
输入：root = []
输出：[]
提示：
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
同上一题，最后翻转结果即可。
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> res;
queue<TreeNode*> que;
if (root != NULL) que.push(root);
TreeNode* cur;
while(!que.empty()){
int size = que.size();
vector<int> subRes;
while(size--){
cur = que.front();
que.pop();
subRes.push_back(cur->val);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
res.push_back(subRes);
}
reverse(res.begin(), res.end());
return res;
}
};
题目链接：199. 二叉树的右视图-中等
题目描述：
给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
层序遍历的时候，判断是否遍历到单层的最后面的元素就可以了。
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
queue<TreeNode*> que;
if (root != NULL)
que.push(root);
TreeNode* cur;
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; ++i) {
cur = que.front();
que.pop();
if (i == (size - 1))
res.push_back(cur->val);
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
}
return res;
}
};
题目链接：637. 二叉树的层平均值-简单
题目描述：
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10^-5 以内的答案可以被接受。
示例 1：
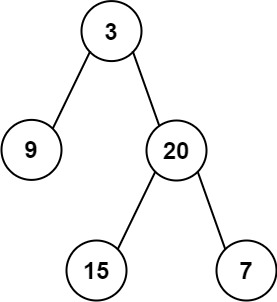
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。
示例 2:
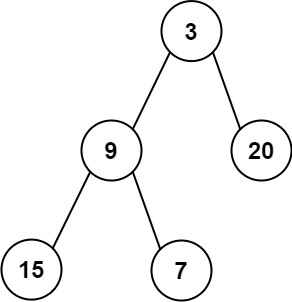
输入：root = [3,9,20,15,7]
输出：[3.00000,14.50000,11.00000]
提示：
- 树中节点数量在
[1, 104]范围内 -2^31 <= Node.val <= 2^31 - 1
层序遍历的时候把一层求个总和在取一个均值
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> res;
queue<TreeNode*> que;
if (root != NULL)
que.push(root);
while (!que.empty()) {
TreeNode* cur;
int size = que.size();
double sum = 0.00000;
for (int i = 0; i < size; ++i) {
cur = que.front();
que.pop();
sum += cur->val;
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
res.push_back(sum / size);
}
return res;
}
};
题目链接：429. N 叉树的层序遍历-中等
题目描述：
给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。
树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。
示例 1：
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]
示例 2：
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
提示：
- 树的高度不会超过
1000 - 树的节点总数在
[0, 10^4]之间
代码如下：
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
queue<Node*> que;
if (root != NULL)
que.push(root);
while (!que.empty()) {
int size = que.size();
Node* cur;
vector<int> subRes;
for (int i = 0; i < size; ++i) {
cur = que.front();
que.pop();
subRes.push_back(cur->val);
for (int i = 0; i < cur->children.size(); ++i) { // 将节点孩子加入队列
que.push(cur->children[i]);
}
}
res.push_back(subRes);
}
return res;
}
};
题目链接：515. 在每个树行中找最大值-中等
题目描述：
给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。
示例1：
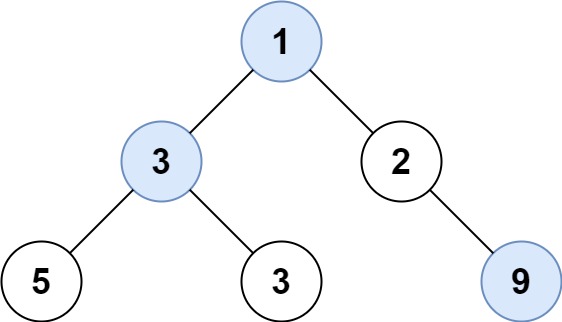
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
示例2：
输入: root = [1,2,3]
输出: [1,3]
提示：
- 二叉树的节点个数的范围是
[0,10^4] -2^31 <= Node.val <= 2^31 - 1
层序遍历，取每一层的最大值
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> res;
queue<TreeNode*> que;
if (root != NULL)
que.push(root);
while (!que.empty()) {
int size = que.size();
TreeNode* cur;
int max = INT_MIN; // 取每一层的最大值
for (int i = 0; i < size; ++i) {
cur = que.front();
que.pop();
max = cur->val > max ? cur->val : max;
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
res.push_back(max);
}
return res;
}
};
题目链接：116. 填充每个节点的下一个右侧节点指针-中等
题目描述：
给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。
示例 1：
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。
示例 2:
输入：root = []
输出：[]
提示：
- 树中节点的数量在
[0, 2^12 - 1]范围内 -1000 <= node.val <= 1000
进阶：
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。
层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了（双指针）
代码如下：
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL)
que.push(root);
while (!que.empty()) {
int size = que.size();
Node* head;
Node* cur;
for (int i = 0; i < size; ++i) {
if (i == 0) {
head = que.front();
que.pop();
cur = head; // 为了将cur的左右孩子节点加入队列
} else {
cur = que.front();
que.pop();
head->next = cur;
head = head->next;
}
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
head->next = NULL;
}
return root;
}
};
题目链接：117. 填充每个节点的下一个右侧节点指针 II-中等
题目描述：
给定一个二叉树：
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。
初始状态下，所有 next 指针都被设置为 NULL 。
示例 1：
输入：root = [1,2,3,4,5,null,7]
输出：[1,#,2,3,#,4,5,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。
示例 2：
输入：root = []
输出：[]
提示：
- 树中的节点数在范围
[0, 6000]内 -100 <= Node.val <= 100
进阶：
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求，本题中递归程序的隐式栈空间不计入额外空间复杂度。
与上题代码一致
代码如下：
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> que;
if (root != NULL)
que.push(root);
while (!que.empty()) {
int size = que.size();
Node* head;
Node* cur;
for (int i = 0; i < size; ++i) {
if (i == 0) {
head = que.front();
que.pop();
cur = head; // 为了将cur的左右孩子节点加入队列
} else {
cur = que.front();
que.pop();
head->next = cur;
head = head->next;
}
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
head->next = NULL;
}
return root;
}
};
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if (root == NULL)
return root;
// 定义一个队列
queue<Node*> que;
que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; ++i) {
Node* cur = que.front();
que.pop();
if (i == size - 1) {
// 每一层的最后一个节点，设置为NULL
cur->next = NULL;
} else {
// 非最后一个节点，设置指向下一个节点，即队列的首元素
cur->next = que.front();
}
// 把下一层节点入队
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
}
return root;
}
};
题目链接：104. 二叉树的最大深度-简单
题目描述：
给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：3
示例 2：
输入：root = [1,null,2]
输出：2
提示：
- 树中节点的数量在
[0, 10^4]区间内。 -100 <= Node.val <= 100
层序遍历模板题
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL)
return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()) {
int size = que.size();
TreeNode* cur;
depth++; // 记录深度
for (int i = 0; i < size; ++i) {
cur = que.front();
que.pop();
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
}
}
return depth;
}
};
递归法：
代码如下：
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL)
return 0;
int lDepth = maxDepth(root->left);
int rDepth = maxDepth(root->right);
return max(lDepth, rDepth) + 1;
}
};
class Solution {
int ans = 0;
void dfs(TreeNode *node, int cnt) {
if (node == NULL) return;
++cnt;
ans = max(ans, cnt);
dfs(node->left, cnt);
dfs(node->right, cnt);
}
public:
int maxDepth(TreeNode *root) {
dfs(root, 0);
return ans;
}
};
题目链接：111. 二叉树的最小深度-简单
题目描述：
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。
示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：2
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
提示：
- 树中节点数的范围在
[0, 10^5]内 -1000 <= Node.val <= 1000
当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == NULL)
return 0;
int depth = 0;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()) {
int size = que.size();
depth++; // 记录最小深度
for (int i = 0; i < size; ++i) {
TreeNode* cur = que.front();
que.pop();
if (cur->left)
que.push(cur->left);
if (cur->right)
que.push(cur->right);
if (!cur->left && !cur->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出
return depth;
}
}
}
return depth;
}
};
递归法：
代码如下：
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == NULL)
return 0;
int lDepth = minDepth(root->left);
int rDepth = minDepth(root->right);
if (root->left == NULL && root->right != NULL)
return rDepth + 1;
else if (root->left != NULL && root->right == NULL)
return lDepth + 1;
return min(lDepth, rDepth) + 1;
}
};
题目链接：226. 翻转二叉树-简单
题目描述：
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
示例 1：
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]
示例 2：
输入：root = [2,1,3]
输出：[2,3,1]
示例 3：
输入：root = []
输出：[]
提示：
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
递归法：
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
swap(root->left, root->right); // 中
invertTree(root->left); // 左
invertTree(root->right); // 右
return root;
}
};
还可按前序遍历、后序遍历、中序遍历、层序遍历这些迭代法做。
题目链接：101. 对称二叉树-简单
题目描述：
给你一个二叉树的根节点 root ， 检查它是否轴对称。
示例 1：
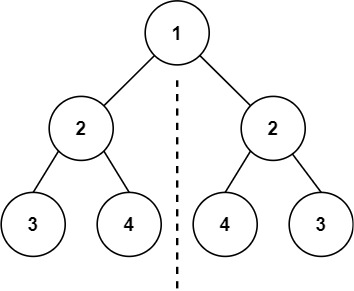
输入：root = [1,2,2,3,4,4,3]
输出：true
示例 2：
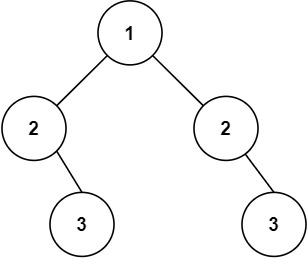
输入：root = [1,2,2,null,3,null,3]
输出：false
提示：
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
进阶：你可以运用递归和迭代两种方法解决这个问题吗？
递归法：
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
bool isSame(TreeNode* left, TreeNode* right) {
if (left == NULL && right == NULL)
return true;
else if (left == NULL || right == NULL || left->val != right->val)
return false;
return isSame(left->left, right->right) && isSame(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if (root == NULL)
return true;
return isSame(root->left, root->right);
}
};
迭代法：
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
queue<TreeNode*> que;
if (root == NULL) return true;
que.push(root->left);
que.push(root->right);
while(!que.empty()){
TreeNode* lNode = que.front(); que.pop();
TreeNode* rNode = que.front(); que.pop();
if(lNode == NULL && rNode == NULL)
continue;
if(lNode == NULL || rNode == NULL || lNode->val != rNode->val)
return false;
que.push(lNode->left);
que.push(rNode->right);
que.push(lNode->right);
que.push(rNode->left);
}
return true;
}
};
题目链接：100. 相同的树-简单
题目描述：
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
示例 1：
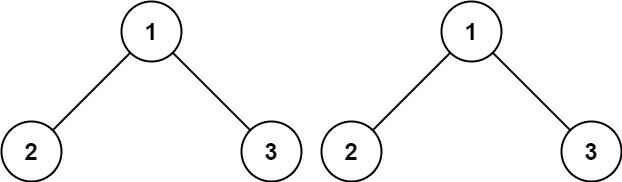
输入：p = [1,2,3], q = [1,2,3]
输出：true
示例 2：
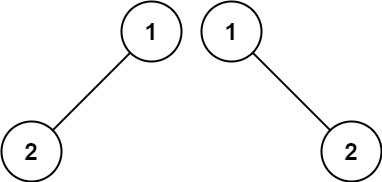
输入：p = [1,2], q = [1,null,2]
输出：false
示例 3：
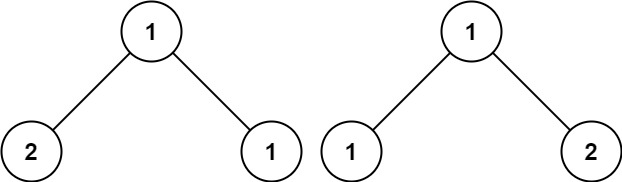
输入：p = [1,2,1], q = [1,1,2]
输出：false
提示：
- 两棵树上的节点数目都在范围
[0, 100]内 -10^4 <= Node.val <= 10^4
同上题，只需要改为对比左的左，右的右即可，迭代法同
递归法：
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL)
return true;
else if (p == NULL || q == NULL || p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
迭代法：
代码如下：
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
queue<TreeNode*> que;
if (p == NULL && q == NULL) return true;
que.push(p);
que.push(q);
while(!que.empty()){
TreeNode* pNode = que.front(); que.pop();
TreeNode* qNode = que.front(); que.pop();
if(pNode == NULL && qNode == NULL)
continue;
if(pNode == NULL || qNode == NULL || pNode->val != qNode->val)
return false;
que.push(pNode->left);
que.push(qNode->left);
que.push(pNode->right);
que.push(qNode->right);
}
return true;
}
};
题目链接：572. 另一棵树的子树-简单
题目描述：
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1：
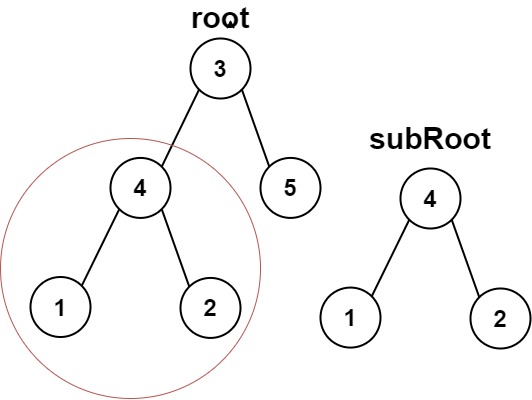
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true
示例 2：
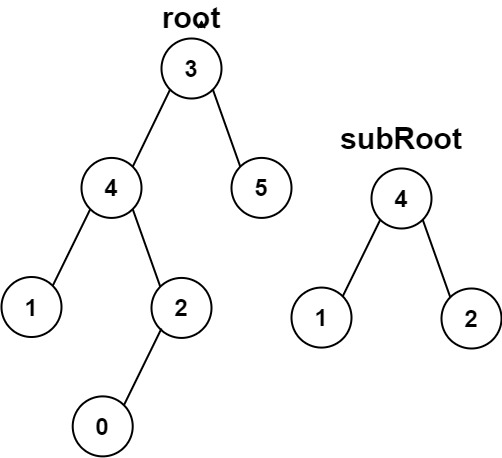
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false
提示：
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-10^4 <= root.val <= 10^4-10^4 <= subRoot.val <= 10^4
递归+迭代法：
代码如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL)
return true;
else if (p == NULL || q == NULL || p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
bool isSame = false;
queue<TreeNode*> que;
que.push(root);
while(!que.empty()){
TreeNode* cur = que.front();
que.pop();
if (cur->val == subRoot->val)
isSame = isSame || isSameTree(cur, subRoot);
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
}
return isSame;
}
};
双重递归法：
代码如下：
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == NULL && q == NULL)
return true;
else if (p == NULL || q == NULL || p->val != q->val)
return false;
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
if (root == NULL)
return false;
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot) || isSameTree(root, subRoot);
}
};
