代码随想录算法训练营day08 | leetcode 344. 反转字符串、541. 反转字符串 II、54. 替换数字、151. 反转字符串中的单词、55. 右旋字符串

目录

题目链接：344. 反转字符串-简单

题目描述：

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

示例 1：

输入：s = ["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：s = ["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

提示：

  • 1 <= s.length <= 10^5
  • s[i] 都是 ASCII 码表中的可打印字符

代码如下：

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
    void reverseString(vector<char>& s) {
        int i = 0, j = s.size() - 1;
        while(i < j){
            swap(s[i], s[j]);
            ++i;
            --j;
        }
    }
};

题目链接：541. 反转字符串 II-简单

题目描述：

给定一个字符串 s 和一个整数 k，从字符串开头算起，每计数至 2k 个字符，就反转这 2k 字符中的前 k 个字符。

  • 如果剩余字符少于 k 个，则将剩余字符全部反转。
  • 如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。

示例 1：

输入：s = "abcdefg", k = 2
输出："bacdfeg"

示例 2：

输入：s = "abcd", k = 2
输出："bacd"

提示：

  • 1 <= s.length <= 104
  • s 仅由小写英文组成
  • 1 <= k <= 10^4

也可以自己实现reverse函数，同上题

代码如下：

// 时间复杂度：O(n)
// 空间复杂度：O(1)
class Solution {
public:
    string reverseStr(string s, int k) {
        for(int i = 0; i < s.size(); i += (2 * k))
        {
            if(i + k <= s.size())
                reverse(s.begin() + i, s.begin() + i + k);
            else
                reverse(s.begin() + i, s.end());
        }
        return s;
    }
};

题目链接：[54. 替换数字](题目页面 (kamacoder.com))

题目描述：

给定一个字符串 s，它包含小写字母和数字字符，请编写一个函数，将字符串中的字母字符保持不变，而将每个数字字符替换为number。 例如，对于输入字符串 "a1b2c3"，函数应该将其转换为 "anumberbnumbercnumber"。

输入描述

输入一个字符串 s,s 仅包含小写字母和数字字符。

输出描述

打印一个新的字符串，其中每个数字字符都被替换为了number

输入示例

a1b2c3

输出示例

anumberbnumbercnumber

提示信息

数据范围：
1 <= s.length < 10000。

img

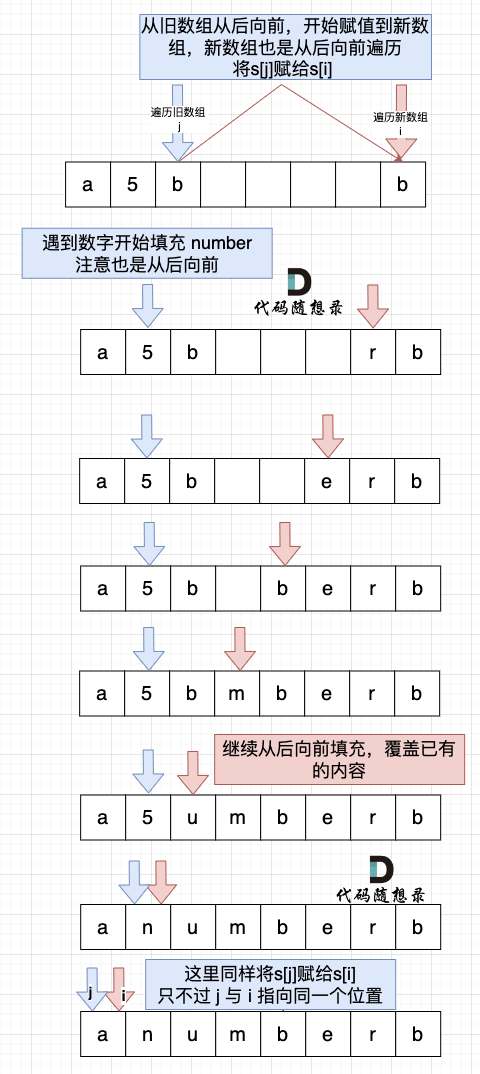
为什么要从后向前填充，而不是从前往后填充

从前向后填充就是O(n^2)的算法了，因为每次添加元素都要将添加元素之后的所有元素整体向后移动。

其实很多数组填充类的问题，其做法都是先预先给数组扩容带填充后的大小，然后在从后向前进行操作。

这么做有两个好处：

  1. 不用申请新数组。
  2. 从后向前填充元素，避免了从前向后填充元素时，每次添加元素都要将添加元素之后的所有元素向后移动的问题。

代码如下：

// 时间复杂度：O(n)
// 空间复杂度：O(1)
#include<iostream>
using namespace std;
int main() {
    string s;
    while (cin >> s) {
        int count = 0; // 统计数字的个数
        int iOldSize = s.size();
        for (int i = 0; i < iOldSize; ++i) {
            if (s[i] >= '0' && s[i] <= '9') {
                ++count;
            }
        }
        // 扩充字符串s的大小，也就是每个空格替换成"number"之后的大小
        int iNewSize = iOldSize + count * 5;
        s.resize(iNewSize);
        // 从后先前将空格替换为"number"
        for (int i = iNewSize - 1, j = iOldSize - 1; j >= 0; --i, --j) {
            if (s[j] > '9' || s[j] < '0') {
                s[i] = s[j];
            } else {
                s[i] = 'r';
                s[i - 1] = 'e';
                s[i - 2] = 'b';
                s[i - 3] = 'm';
                s[i - 4] = 'u';
                s[i - 5] = 'n';
                i -= 5;
            }
        }
        cout << s << endl;
    }
}

题目链接：151. 反转字符串中的单词-中等

题目描述：

给你一个字符串 s ，请你反转字符串中 单词 的顺序。

单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。

返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。

注意：输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。

示例 1：

输入：s = "the sky is blue"
输出："blue is sky the"

示例 2：

输入：s = "  hello world  "
输出："world hello"
解释：反转后的字符串中不能存在前导空格和尾随空格。

示例 3：

输入：s = "a good   example"
输出："example good a"
解释：如果两个单词间有多余的空格，反转后的字符串需要将单词间的空格减少到仅有一个。

提示：

  • 1 <= s.length <= 104
  • s 包含英文大小写字母、数字和空格 ' '
  • s 中 至少存在一个 单词

进阶：如果字符串在你使用的编程语言中是一种可变数据类型，请尝试使用 O(1) 额外空间复杂度的 原地 解法。

步骤：

  • 去除空格
  • 整体翻转
  • 局部翻转

代码如下：

// 时间复杂度：O(n)
// 空间复杂度: O(1) 或 O(n)，取决于语言中字符串是否可变
class Solution {
public:
    void reverse(string& s, int start, int end){
        for(int i = start, j = end; i < j; ++i, --j){
            swap(s[i], s[j]);
        }
    }
    void removeSpaces(string& s){
        int slow = 0;
        for(int fast = 0; fast < s.size(); ++fast){
            // 遇到要删除的元素，fast指针继续往下走，即不做任何处理
            if(s[fast] != ' '){ // 遇到非空格就处理，即删除所有空格。
                if(slow != 0) s[slow++] = ' '; // 手动控制空格，给单词之间添加空格。slow != 0说明不是第一个单词，需要在单词前添加空格。
                while(fast < s.size() && s[fast] != ' ')
                    s[slow++] = s[fast++]; // 补上该单词，遇到空格说明单词结束。
            }
        }
        s.resize(slow);
    }
    string reverseWords(string s) {
        removeSpaces(s);
        reverse(s, 0, s.size() - 1);
        int subStart = 0;
        for(int i = 0; i <= s.size(); ++i){
            if(s[i] == ' ' || i == s.size()){
                reverse(s, subStart, i - 1);
                subStart = i + 1;
            }
        }
        return s;
    }
};

题目链接：[55. 右旋字符串](题目页面 (kamacoder.com))

题目描述：

字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k，请编写一个函数，将字符串中的后面 k 个字符移到字符串的前面，实现字符串的右旋转操作。 

例如，对于输入字符串 "abcdefg" 和整数 2，函数应该将其转换为 "fgabcde"。

输入描述

输入共包含两行，第一行为一个正整数 k，代表右旋转的位数。第二行为字符串 s，代表需要旋转的字符串。

输出描述

输出共一行，为进行了右旋转操作后的字符串。

输入示例

2
abcdefg

输出示例

fgabcde

提示信息

数据范围：
1 <= k < 10000,
1 <= s.length < 10000;

步骤：

  • 整体翻转
  • 翻转前一段
  • 翻转后一段

代码如下：

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main()
{
    int k;
    string s;
    while(cin >> k >> s)
    {
        if(k > s.size()) return 0;
        reverse(s.begin(), s.end()); // 整体反转
        reverse(s.begin(), s.begin() + k); // 先反转前一段，长度n
        reverse(s.begin() + k, s.end()); // 再反转后一段
        cout << s <<endl;
    }
}
posted @ 2024-02-28 23:03  Humphreyr  阅读(9)  评论(0)  编辑  收藏  举报