Java中二叉树的遍历、查找

1、准备节点

/**
 * 二叉树的节点
 * @author lurenjia
 * @date 2022/12/7-12:07
 */
public class Node {
    Object value;
    Node leftChild;
    Node rightChild;

    public Node(Object o){
        value = o;
    }

    public Node(Object value, Node leftChild, Node rightChild) {
        this.value = value;
        this.leftChild = leftChild;
        this.rightChild = rightChild;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                ", leftChild=" + leftChild +
                ", rightChild=" + rightChild +
                '}';
    }
}

2、实现对二叉树的操作

import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;

/**
 * 二叉树实现
 * @author lurenjia
 * @date 2022/12/7-12:10
 */
public class BinaryTree {
    private Node root;//根节点

    public BinaryTree(Node root) {    this.root = root;}

    public BinaryTree() {}

    /**
     * 判断二叉树是否为空，为空返回true
     * @return
     */
    public boolean isEmpty(){   return root==null;}

    /**
     * 中序遍历
     */
    public void LDRtraverse(){
        System.out.print("中序遍历，使用递归实现：");
        this.LDRtraverse(root);
        System.out.println();
    }
    private void LDRtraverse(Node root){
        if(root!=null){
            //1、遍历左子树
            this.LDRtraverse(root.leftChild);
            //2、输出根
            System.out.print(root.value+" ");
            //3、遍历右子树
            this.LDRtraverse(root.rightChild);
        }
    }

    /**
     * 中序遍历二叉树，使用栈（后进先出）实现。
     */
    public void LDRtraverseByStack(){
        System.out.print("中序遍历，使用栈实现：");
        //1、创建栈
        Deque<Node> stack = new LinkedList<>();
        //2、获取根节点
        Node current = root;
        //若根节点不为空，或者栈不为空则进入循环
        while ( current!=null || !stack.isEmpty()){

            //如果不为空节点，则入栈，而后判断左子节点是否存在，存在则入栈，最终左下角的元素在栈首
            while (current!=null){
                stack.push(current);
                current = current.leftChild;
            }

            //如果栈不为空，则出栈一个（即左下角元素），节点指向出栈的右子节点
            if(!stack.isEmpty()){
                current = stack.pop();
                System.out.print(current.value+" ");
                current = current.rightChild;
            }
        }
        System.out.println();
    }
    /**
     * 获取二叉树的高度
     * @return
     */
    public int getHeight(){ return this.getHeight(root); }
    private int getHeight(Node root){
        if(root==null){
            return 0;
        }else{
            //1、获取左子树的高度
            int nl = this.getHeight(root.leftChild);
            //2、获取右子树的高度
            int nr = this.getHeight(root.rightChild);
            //3、其中大的高度，加一，获取
            return nl>nr?nl+1:nr+1;
        }
    }

    /**
     * 获取二叉树内节点个数
     * @return
     */
    public int size(){  return this.size(root); }
    private int size(Node root){
        if(root==null){
            return 0;
        }else {
            //1、获取左子树的结点个数
            int nl = this.size(root.leftChild);
            //2、获取右子树的结点个数
            int nr = this.size(root.rightChild);
            //3、返回个数
            return nl+nr+1;
        }
    }

    /**
     * 在树中寻找对应的元素
     * @param value
     * @return
     */
    public Node findKey(Object value){
        return this.findKey(value,root);
    }
    private Node findKey(Object value,Node root){
        if(root==null){//递归头1：为空树
            return null;
        }else if(root!=null&&root.value==value){
            //递归头2：找到了目标元素
            return root;
        }else {//递归体
            //遍历左子树
            Node node1 = this.findKey(value,root.leftChild);
            //遍历右子树
            Node node2 = this.findKey(value,root.rightChild);

            if(node1!=null&&node1.value==value){
                return node1;
            }else if(node2!=null&&node2.value==value){
                return node2;
            }else {//没找到
                return null;
            }
        }
    }

    /**
     * 按照层次遍历二叉树，使用队列（先进先出）实现。
     */
    public void levelOrderByStack(){
        System.out.print("按照层次遍历二叉树，使用队列实现：");
        if(root==null)return;
        //1、创建队列
        Queue<Node> queue = new LinkedList<>();
        //2、根节点入队
        queue.add(root);
        //队列中有元素则进入循环
        while (queue.size()!=0){
            //按照栈中元素的个数进行出队循环
            int len = queue.size();
            for(int i = 0;i<len;i++){
                //根节点出队
                Node temp = queue.poll();
                System.out.print(temp.value+" ");
                //如果根节点有左子节点，左子节点入队
                if(temp.leftChild!=null) queue.add(temp.leftChild);
                //如果根节点有左子节点，左子节点入队
                if(temp.rightChild!=null) queue.add(temp.rightChild);
            }
        }
        System.out.println();
    }
}

3、测试代码： 

/**
 * @author lurenjia
 * @date 2022/12/7-12:23
 */
public class User {
    public static void main(String[] args) {
        //手动创建节点
        Node node7 = new Node("G",null,null);
        Node node4 = new Node("D",null,null);
        Node node5 = new Node("E",node7,null);
        Node node6 = new Node("F",null,null);
        Node node2 = new Node("B",node4,node5);
        Node node3 = new Node("C",null,node6);
        Node node1 = new Node("A",node2,node3);
        //通过根节点创建一个二叉树对象
        BinaryTree btree = new BinaryTree(node1);
        //判断是否为空
        System.out.println("是否为空："+btree.isEmpty());
        //获取高度
        System.out.println("此二叉树的高度为："+btree.getHeight());
        //获取节点个数
        System.out.println("此二叉树的节点个数为:"+btree.size());
        //中序遍历,递归实现
        btree.LDRtraverse();
        //中序遍历，
        btree.LDRtraverseByStack();
        //按照层次遍历
        btree.levelOrderByStack();
        //查找指定元素
        System.out.println("查找："+btree.findKey("E"));
    }
}

 

测试代码中创建的二叉树：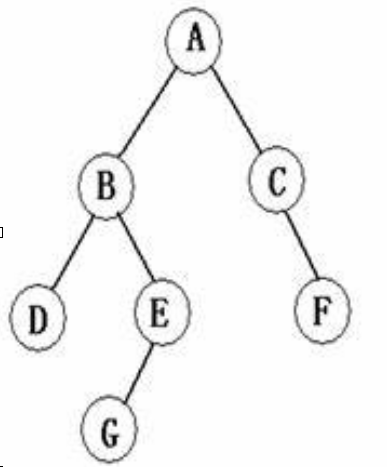

 

 

 

测试结果：

是否为空：false
此二叉树的高度为：4
此二叉树的节点个数为:7
中序遍历，使用递归实现：D B G E A C F 
中序遍历，使用栈实现：D B G E A C F 
按照层次遍历二叉树，使用队列实现：A B C D E F G 
查找：Node{value=E, leftChild=Node{value=G, leftChild=null, rightChild=null}, rightChild=null}

Process finished with exit code 0