动态dp & 矩阵加速递推
前言
对于动态 dp / 矩阵加速递推的题目，我们一般可以先从暴力 dp 转移式入手，（转化为）一个容易使用矩阵乘处理的式子，从而达到使用数据结构维护或使用倍增/快速幂加速递推的效果。
广义矩阵乘法
我们定义两个矩阵 \(A,B\) 在广义矩阵乘法下的乘积为 \(C\)，其中
\[C = \begin{bmatrix} \max\limits_{i=1}\limits^{m} A_{1,i} + B_{i,1} & \max\limits_{i=1}\limits^{m} A_{1,i} + B_{i,2} & \dots & \max\limits_{i=1}\limits^{m} A_{1,i} + B_{i,k} \\\ \max\limits_{i=1}\limits^{m} A_{2,i} + B_{i,1} & \max\limits_{i=1}^{m} A_{2,i} + B_{i,2} & \dots & \max\limits_{i=1}\limits^{m} A_{2,i} + B_{i,k} \\\ \vdots & \vdots & \ddots & \vdots \\\ \max\limits_{i=1}\limits^{m} A_{n,i} + B_{i,1} & \max\limits_{i=1}\limits^{m} A_{n,i} +
B_{i,2} & \dots & \max\limits_{i=1}\limits^{m} A_{n,i}+ B_{i,k}\end{bmatrix}\]
这么定义矩阵乘法是为了改写某些 DP 柿子。不难发现这个乘法依然具有结合律。
\(\max\) 改为 \(\min\) 同理。
动态 dp
引入
有一个序列 \(a\)，你可以在其中选择一些数，但是你不能选择相邻的两个数，求你能选出的数的总和最大是多少。
我们令 \(dp_{i,0/1}\) 为考虑前 \(i\) 个数，选或不选第 \(i\) 个数的最大和。
不难得到 \(dp_{i,0}=\max(dp_{i-1,0},dp_{i-1,1}),dp_{i,1}=dp_{i-1,0}+a_i\)。
那么这跟我们上面所说的矩阵乘法有什么关系呢？
我们将 dp 式改写一下：
\[dp_{i,0}=\max(dp_{i-1,0}+0,dp_{i-1,1}+0)
\]
\[dp_{i,1}=\max(dp_{i-1,0}+a_i,dp_{i-1,1} - \infty)
\]
现在是不是和上述的广义矩阵乘法很像了？我们将 dp 继续改写为矩阵乘的形式：
\[\begin{bmatrix} dp_{i-1,0} & dp_{i-1,1} \end{bmatrix} \times \begin{bmatrix} 0 & a_i \\\ 0 & - \infty \end{bmatrix} = \begin{bmatrix} dp_{i,0} & dp_{i,1} \end{bmatrix}
\]
由于矩阵乘具有结合律，所以我们现在可以将 dp 结果写成一系列矩阵连乘的结果了！
但是我们这么做却不是为了优化时间复杂度，而是为了：
带修
如果我们将引入题改一下，增加 \(m\) 次单点修改 \(a_i\) 的值，怎么做？
我们只需要使用线段树维护上述的矩阵乘法即可！！！
例题 Gym102644H String Mood Updates
首先我们考虑暴力 dp。
我们令 \(dp_{i,0/1}\) 代表读完前 \(i\) 个字符后当前状态为 \(0/1\) 的方案数。转移有：
\[\begin{cases}dp_{i,0}=dp_{i-1,0}+dp_{i-1,1},dp_{i,1}=0 \space\space s_i=\texttt{S,D} \\\ dp_{i,0}=0,dp_{i,1}=dp_{i-1,0}+dp_{i-1,1} \space\space s_i=\texttt{H} \\\ dp_{i,0}=dp_{i-1,1},dp_{i,1}=dp_{i-1,0} \space\space s_i=\texttt{A,E,I,O,U} \\\ dp_{i,0}=20 \times dp_{i-1,0} + 7 \times dp_{i-1,1},dp_{i-1,1}=6 \times dp_{i-1,0} + 19 \times dp_{i-1,1} \space\space s_i=\texttt{?} \\\ dp_{i,0}=dp_{i-1,0},dp_{i,1}=dp_{i-1,1} \space\space \operatorname{otherwise}\end{cases}
\]
带修的话，根据这个状态转移，构建出转移矩阵，并用线段树维护即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
#define fi first
#define sc second
#define pii pair<int,int>
#define pb push_back
const int maxn=2e5+10;
const int mod=1e9+7;
int n,m,dp[maxn][2];
string s;
struct mat{
int n,a[3][3];
void init(int x){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) a[i][j]=x;
}
}
void getI(){
init(0);
for(int i=1;i<=n;i++) a[i][i]=1;
}
mat operator *(mat x){
mat ans;
ans.n=n,ans.init(0);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
ans.a[i][j]=(ans.a[i][j]+a[i][k]*x.a[k][j])%mod;
}
}
}
return ans;
}
void output(){
for(int i=1;i<=n;i++,cout<<endl){
for(int j=1;j<=n;j++) cout<<a[i][j]<<" ";
}
}
};
struct node{
int l,r;
mat mt;
node operator +(node x){
if(l==-1) return x;
if(x.l==-1) return (*this);
node res;
res.l=l,res.r=x.r,res.mt=(mt*x.mt);
return res;
}
void debug(){
cout<<l<<" "<<r<<endl;
cout<<"MATRIX:"<<endl;
mt.output();
cout<<endl;
}
}tr[maxn*4];
int ls(int u){
return (u<<1);
}
int rs(int u){
return (u<<1)|1;
}
bool ir(int L,int R,int l,int r){
return (L<=l)&&(r<=R);
}
bool ofr(int L,int R,int l,int r){
return (R<l)||(r<L);
}
void pushup(int u){
if(tr[u].l==tr[u].r) return ;
tr[u]=tr[ls(u)]+tr[rs(u)];
}
void build(int u,int l,int r){
tr[u].l=l,tr[u].r=r,tr[u].mt.n=2;
if(l==r){
if(s[l]=='S'||s[l]=='D'){
tr[u].mt.a[1][1]=1,tr[u].mt.a[1][2]=0;
tr[u].mt.a[2][1]=1,tr[u].mt.a[2][2]=0;
}
else if(s[l]=='H'){
tr[u].mt.a[1][1]=0,tr[u].mt.a[1][2]=1;
tr[u].mt.a[2][1]=0,tr[u].mt.a[2][2]=1;
}
else if(s[l]=='A'||s[l]=='E'||s[l]=='I'||s[l]=='O'||s[l]=='U'){
tr[u].mt.a[1][1]=0,tr[u].mt.a[1][2]=1;
tr[u].mt.a[2][1]=1,tr[u].mt.a[2][2]=0;
}
else if(s[l]=='?'){
tr[u].mt.a[1][1]=20,tr[u].mt.a[1][2]=6;
tr[u].mt.a[2][1]=7,tr[u].mt.a[2][2]=19;
}
else{
tr[u].mt.a[1][1]=1,tr[u].mt.a[1][2]=0;
tr[u].mt.a[2][1]=0,tr[u].mt.a[2][2]=1;
}
return ;
}
int mid=(l+r)>>1;
build(ls(u),l,mid),build(rs(u),mid+1,r),pushup(u);
}
void upd(int u,int x,char k){
if(tr[u].l==tr[u].r){
if(k=='S'||k=='D'){
tr[u].mt.a[1][1]=1,tr[u].mt.a[1][2]=0;
tr[u].mt.a[2][1]=1,tr[u].mt.a[2][2]=0;
}
else if(k=='H'){
tr[u].mt.a[1][1]=0,tr[u].mt.a[1][2]=1;
tr[u].mt.a[2][1]=0,tr[u].mt.a[2][2]=1;
}
else if(k=='A'||k=='E'||k=='I'||k=='O'||k=='U'){
tr[u].mt.a[1][1]=0,tr[u].mt.a[1][2]=1;
tr[u].mt.a[2][1]=1,tr[u].mt.a[2][2]=0;
}
else if(k=='?'){
tr[u].mt.a[1][1]=20,tr[u].mt.a[1][2]=6;
tr[u].mt.a[2][1]=7,tr[u].mt.a[2][2]=19;
}
else{
tr[u].mt.a[1][1]=1,tr[u].mt.a[1][2]=0;
tr[u].mt.a[2][1]=0,tr[u].mt.a[2][2]=1;
}
return ;
}
int mid=(tr[u].l+tr[u].r)>>1;
if(x<=mid) upd(ls(u),x,k);
else upd(rs(u),x,k);
pushup(u);
}
void solve(){
cin>>n>>m>>s,s=" "+s;
build(1,1,n);
// tr[1].mt.output();
cout<<tr[1].mt.a[2][2]<<endl;
while(m--){
int x;
char c;
cin>>x>>c,upd(1,x,c);
// tr[1].mt.output();
cout<<tr[1].mt.a[2][2]<<endl;
// for(int i=1;i<n*2;i++) tr[i].debug();
// cout<<endl;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
while(t--) solve();
return 0;
}
/*
Samples
input:
output:
THINGS TODO:
检查freopen，尤其是后缀名
检查空间
检查调试语句是否全部注释
*/
【模板】"动态 DP"&动态树分治
令 \(dp_{u,0/1}\) 为选/不选节点 \(u\) 的最大独立集权值，我们还是先考虑暴力 dp 的转移式：
\(\begin{cases}dp_{u,0}=\sum\limits_{v \in son_u} \max(dp_{v,0},dp_{v,1}) \\\ dp_{u,1}=w_u + \sum\limits_{v \in son_u} dp_{v,0} \end{cases}\)
我们发现如果我们对一个点 \(x\) 做单点修改，我们将要重新计算 \(x\) 到根节点路径上的所有点的 \(dp\) 值。
所以我们考虑如何来优化重算 dp 值的过程。
我们对于这样一棵树：
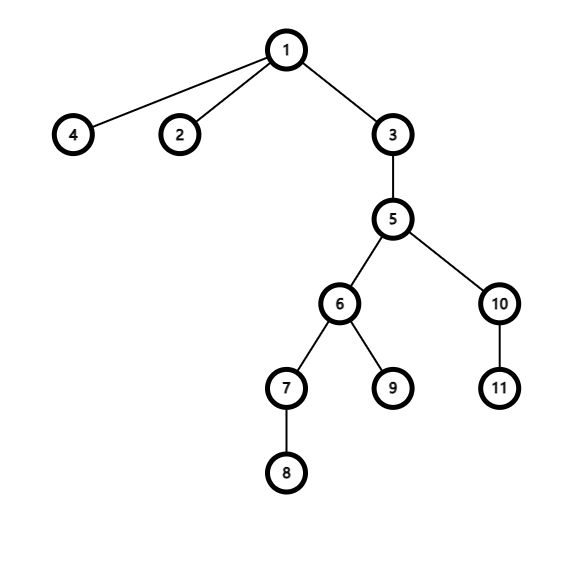
我们暂时只考虑根节点 \(1\) 所在的重链 \(1-3-5-6-7-8\) 的贡献，然后将其它轻儿子的贡献加上。
所以我们记 \(f_{i,0/1}\) 代表选/不选节点 \(u\) 且不选 \(u\) 的重儿子的最大独立集权值，这样我们就会有 \(\begin{cases}dp_{u,0}=f_{u,0} + \max(dp_{hson_u,0},dp_{hson_u,1})) \\\ dp_{u,1}=f_{u,1} + dp_{hson_u,0} \end{cases}\)
其中 \(hson_u\) 为 \(u\) 的重儿子。
可以发现：现在我们的 dp 式好像长得又跟矩阵乘法式很像了！我们对于每一条重链，都有：
\[\begin{bmatrix} dp_{hson_u,0} & dp_{hson_u,1} \end{bmatrix} \times \begin{bmatrix} f_{u,0} & f_{u,1} \\\ f_{u,0} & - \infty \end{bmatrix} = \begin{bmatrix} dp_{u,0} & dp_{u,1} \end{bmatrix}
\]
所以我们可以考虑开线段树维护每一条重链的矩阵乘法，这样我们在修改一个点 \(x\) 的时候，我们只需要修改 \(x\) 到根节点路径上的所有重链的信息即可，时间复杂度 \(O(n \log^2 n)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
#define fi first
#define sc second
#define pii pair<int,int>
#define pb push_back
const int maxn=1e5+10;
const int inf=1e9;
int n,m,w[maxn],sz[maxn],son[maxn],tp[maxn],ed[maxn],dfn[maxn],dep[maxn],cnt,dp[maxn][2],f[maxn];
vector<int> g[maxn];
struct mat{
int n,a[3][3];
void init(int x){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) a[i][j]=x;
}
}
void getI(){
init(-inf);
for(int i=1;i<=n;i++) a[i][i]=0;
}
mat operator *(mat x){
mat ans;
ans.n=n,ans.init(-inf);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
ans.a[i][j]=max(ans.a[i][j],a[i][k]+x.a[k][j]);
}
}
}
return ans;
}
void output(){
cout<<"----MATRIXS----"<<endl;
for(int i=1;i<=n;i++,cout<<endl){
for(int j=1;j<=n;j++) cout<<a[i][j]<<" ";
}
cout<<"------END------"<<endl;
}
}val[maxn],I;
struct node{
int l,r;
mat s;
}tr[maxn*4];
int ls(int u){
return (u<<1);
}
int rs(int u){
return (u<<1)|1;
}
bool ir(int L,int R,int l,int r){
return (L<=l)&&(r<=R);
}
bool ofr(int L,int R,int l,int r){
return (R<l)||(r<L);
}
void dfs1(int u,int fa){
sz[u]=1,dep[u]=dep[fa]+1,dp[u][1]=w[u],f[u]=fa;
for(int v:g[u]){
if(v!=fa){
dfs1(v,u),sz[u]+=sz[v];
if(sz[v]>sz[son[u]]) son[u]=v;
dp[u][0]+=max(dp[v][0],dp[v][1]);
dp[u][1]+=dp[v][0];
}
}
}
void dfs2(int u,int fa,int top){
tp[u]=top,dfn[u]=++cnt,val[dfn[u]].n=2;
if(son[u]) dfs2(son[u],u,top);
val[dfn[u]].a[2][2]=-inf,val[dfn[u]].a[1][2]=w[u];
for(int v:g[u]){
if(v!=fa&&v!=son[u]){
dfs2(v,u,v);
val[dfn[u]].a[1][1]+=max(dp[v][0],dp[v][1]);
val[dfn[u]].a[2][1]+=max(dp[v][0],dp[v][1]);
val[dfn[u]].a[1][2]+=dp[v][0];
}
}
if(!son[u]) ed[u]=u;
else ed[u]=ed[son[u]];
}
void pushup(int u){
if(tr[u].l==tr[u].r) return ;
tr[u].s=tr[rs(u)].s*tr[ls(u)].s;
}
void build(int u,int l,int r){
tr[u].l=l,tr[u].r=r;
if(l==r) return tr[u].s=val[l],void();
int mid=(l+r)>>1;
build(ls(u),l,mid),build(rs(u),mid+1,r),pushup(u);
}
void upd(int u,int x,mat k){
if(tr[u].l==tr[u].r) return tr[u].s=k,void();
int mid=(tr[u].l+tr[u].r)>>1;
if(x<=mid) upd(ls(u),x,k);
else upd(rs(u),x,k);
pushup(u);
}
mat query(int u,int l,int r){
if(ir(l,r,tr[u].l,tr[u].r)) return tr[u].s;
else if(!ofr(l,r,tr[u].l,tr[u].r)) return query(rs(u),l,r)*query(ls(u),l,r);
else return I;
}
void cover(int u,int k){
val[dfn[u]].a[1][2]-=w[u],w[u]=k,val[dfn[u]].a[1][2]+=w[u];
while(u){
mat m1=query(1,dfn[tp[u]],dfn[ed[u]]),m2;
upd(1,dfn[u],val[dfn[u]]),m2=query(1,dfn[tp[u]],dfn[ed[u]]);
u=f[tp[u]];
/*
[fi,0 fi,1]
[fi,0 -inf]
*/
val[dfn[u]].a[1][1]-=max(m1.a[1][1],m1.a[1][2]);
val[dfn[u]].a[1][1]+=max(m2.a[1][1],m2.a[1][2]);
val[dfn[u]].a[2][1]=val[dfn[u]].a[1][1];
val[dfn[u]].a[1][2]-=m1.a[1][1];
val[dfn[u]].a[1][2]+=m2.a[1][1];
}
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
for(int i=1,u,v;i<n;i++) cin>>u>>v,g[u].pb(v),g[v].pb(u);
dfs1(1,0),dfs2(1,0,1),build(1,1,n);
// for(int i=1;i<=n;i++) cout<<tp[i]<<" ";
// cout<<endl;
while(m--){
int x,y;
cin>>x>>y;
cover(x,y);
mat res=query(1,1,dfn[ed[1]]);
cout<<max(res.a[1][1],res.a[1][2])<<endl;
}
}
signed main(){
// freopen("P4719_4.in","r",stdin);
// freopen("out.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t=1;
// cin>>t;
I.n=2,I.getI();
while(t--) solve();
return 0;
}
/*
Samples
input:
output:
THINGS TODO:
检查freopen，尤其是后缀名
检查空间
检查调试语句是否全部注释
*/
矩阵加速递推
例题1 Graph Paths II
我们令 \(dp_{i,j}\) 为已经走了 \(i\) 条边，终点为 \(j\) 的最短路。对于每一条 \(u \to v\)，边权为 \(w\) 的边，我们都有 \(dp_{i,v}=\min(dp_{i-1,u}+w)\)。
我们发现对于每一次转移，转移边是不变的。所以我们可以考虑矩阵快速幂优化 dp。
