图论合集
最短路算法
全源最短路
问题
给出一张图
Floyd 算法
我们令
那么初始化
容易得到
那么
显然第一维对于答案没有影响,那么压掉之后空间就优化成了
时间复杂度
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
}
}
}
单源最短路
Dijkstra 算法
Dijkstra 可以求出一个非负权边图的一个点
令
初始化所有
重复执行以下操作,直到每个点的最短路都确定:
-
从所有不确定最短路的点中,选取一个当前最短路最小的点,此时可以证明它的当前最短路就是它的最短路。
-
更新这个点的所有出边到达的所有点的
时间复杂度为
Dijkstra 的堆优化
不难发现上述操作
将所有松弛到的点丢进一个堆里,每次取堆顶就可以了。
时间复杂度
使用时需要根据图的性质来选择是否使用堆优化。
struct edge{
int to,v;
};
struct node{
int v,w;
bool operator <(node a) const{
return w>a.w;
}
}wsy;
vector<edge> G[maxn];
priority_queue<node> q;
void wsyAKIOI(){
dis[s]=0;
wsy={s,0};
q.push(wsy);
while(q.size()){
int u=q.top().v;
q.pop();
if(vis[u]) continue;
vis[u]=1;
for(int i=0;i<G[u].size();i++){
int v=G[u][i].to,val=G[u][i].v;
if(dis[v]>dis[u]+val){
dis[v]=dis[u]+val;
if(!vis[v]){
wsy={v,dis[v]};
q.push(wsy);
}
}
}
}
}
Bellman-Ford 算法
上述提到了一个松弛式子:
Bellman–Ford 算法所做的,就是不断尝试对图上每一条边进行松弛。我们每进行一轮循环,就对图上所有的边都尝试进行一次松弛操作,当一次循环中没有成功的松弛操作时,算法停止。
不难发现每次操作时
由于一条最短路最多包含
时间复杂度
Bellmax-Ford 算法较于 Dijkstra 的好处就是可以求含负权边图的最短路。
Bellman-Ford 的队列优化——SPFA
不难发现只有上一次被松弛的结点所连接的边才有可能引起下一次的松弛操作。
每次松弛操作的时候塞进一个队列里面,访问的就只有必要的边了。
void spfa(int s){
q.push(s);
inq[s]=114514;
while(q.size()){
int u=q.front();
inq[u]=0;
q.pop();
for(int i=0;i<G[u].size();i++){
int v=G[u][i].e,w=G[u][i].v;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
if(!inq[v]){
inq[v]=1;
q.push(v);
}
}
}
}
}
由于 SPFA 可以被神奇数据卡到
应用
差分约束
差分约束,是由
其中
我们需要对这个
考虑如何来处理这个问题。
我们对约束条件
所以我们便可以对于每个约束条件,连一条
因为我们的图可能不联通,所以我们需要建立一个超级源点
我们又不难注意到对于一组解中的每个数都加上一个常数,得到的仍然是该不等式组的一组解,因为这个常数在做差时会被消掉。
例1【模板】差分约束算法
差分约束模板题。
代码:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m;
const int maxn=5001;
struct node{
int e,v;
};
vector<node> G[maxn+10];
int dis[maxn],cnt[maxn],vis[maxn];
queue<int> q;
bool spfa(int s){
memset(dis,63,sizeof(dis));
dis[s]=0,vis[s]=1;
q.push(s);
while(!q.empty()){
int u=q.front();
q.pop(),vis[u]=0;
for(int i=0;i<G[u].size();i++){
node ed=G[u][i];
int v=ed.e,w=ed.v;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
cnt[v]=cnt[u]+1;
if(cnt[v]>n) return 0;
if(!vis[v]) q.push(v),vis[v]=1;
}
}
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
G[b].push_back((node){a,c});
}
for(int i=1;i<=n;i++){
G[0].push_back((node){i,0});
}
if(!spfa(0)){
puts("NO");
}
else{
for(int i=1;i<=n;i++){
cout<<dis[i]+114514<<" ";
//由于上文提到的性质所以这么做是没问题的
}
}
return 0;
}
例2 小 K 的农场
对于第一种约束,列出不等式
对于第二种约束,列出不等式
对于第三种约束,列出等式
然后 SPFA 即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=5000+10;
int n,m,dis[maxn],inq[maxn],cnt[maxn];
struct edge{
int e,v;
};
vector<edge> G[maxn];
queue<int> q;
bool spfa(int s){
q.push(s);
inq[s]=1;
cnt[s]++;
while(q.size()){
int u=q.front();
q.pop();
inq[u]=0;
for(int i=0;i<G[u].size();i++){
int v=G[u][i].e,w=G[u][i].v;
if(dis[v]>dis[u]+w){
//cout<<"考虑对"<<u<<"->"<<v<<"松弛"<<endl;
dis[v]=dis[u]+w;
//cout<<"松弛后为"<<dis[u]<<endl;
cnt[v]=cnt[u]+1;
if(cnt[v]>n) return 0;
if(!inq[v]){
q.push(v);
inq[v]=1;
}
}
}
}
return 1;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
memset(dis,0x7f,sizeof(dis));
dis[0]=0;
cin>>n>>m;
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int a,b,c;
cin>>a>>b>>c;
G[a].push_back((edge){b,-c});
}
if(op==2){
int a,b,c;
cin>>a>>b>>c;
G[b].push_back((edge){a,c});
}
if(op==3){
int a,b;
cin>>a>>b;
G[a].push_back((edge){b,0});
}
}
for(int i=1;i<=n;i++){
G[0].push_back((edge){i,0});
}
if(spfa(0)) puts("Yes");
else puts("No");
return 0;
}
例3 [1007]倍杀测量者
不难注意到对每个不等式取
即可变形为
显然不可能暴力枚举所有
我们又双叒叕不难注意到答案序列显然有单调性。
所以二分即可,check 函数写个差分约束判一下就行。
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1100;
struct flag{
int op,a,b,k;
}fl[maxn];
struct edge{
int nxt,to,tag;
double w;
}a[maxn<<1];
int n,s,t,c[maxn],fr[maxn],head[maxn],cnt,vis[maxn],gt[maxn];
double l=0,r=1e18,T=-1,dis[maxn];
queue<int> q;
void add(int x,int y,int tag,double w){
a[++cnt]=(edge){head[x],y,tag,log2(w)};
head[x]=cnt;
}
int check(double T){
memset(head,0,sizeof head);
memset(fr,0,sizeof fr);
cnt=0;
while(q.size()){
q.pop();
}
for(int i=1;i<=n;i++){
if(c[i]){
add(i,0,1,c[i]);
add(0,i,0,c[i]);
}
}
for(int i=1;i<=s;i++){
int a=fl[i].a,b=fl[i].b,k=fl[i].k,op=fl[i].op;
if(c[a]&&c[b]&&((op==1&&c[a]<c[b]*(k-T))||(op==2&&c[a]*(k+T)<c[b]))){
return 1;
}
if(op==1){
add(a,b,1,k-T);
}
else{
add(a,b,0,k+T);
}
}
for(int i=0;i<=n;i++){
dis[i]=0;
fr[i]=0;
q.push(i);
vis[i]=1;
}
while(q.size()){
int x=q.front();
for(int i=head[x];i;i=a[i].nxt){
int u=a[i].to;
double w;
if(a[i].tag){
w=dis[x]-a[i].w;
}
else{
w=dis[x]+a[i].w;
}
if(dis[u]<=w&&dis[u]!=-1){
goto luqyou;
}
dis[u]=w;
fr[u]=fr[x]+1;
if(fr[u]==n+2) return 1;
if(!vis[u]){
q.push(u);
vis[u]=1;
}
luqyou:;
}
q.pop();
vis[x]=0;
}
return 0;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>s>>t;
for(int i=1;i<=s;i++){
int op,a,b,k;
cin>>op>>a>>b>>k;
fl[i]=(flag){op,a,b,k};
if(op==1){
r=min(r,(double)k-1e-8);
}
}
for(int i=1;i<=t;i++){
int x,y;
cin>>x>>y;
c[x]=y;
}
while(r-l>1e-6){
double mid=(l+r)/2.0;
if(check(mid)){
l=mid;
T=mid;
}
else{
r=mid;
}
}
if(T==-1){
puts("-1");
}
else{
printf("%.10lf",T);
}
return 0;
}
套路题——分层图
例题1 [JLOI2011] 飞行路线
可以发现
考虑建分层图。
每一层就是原图,然后在每相邻两层,且有直接联通的两点之间连接一个边权为
然后 Dij 求点
连通性问题
割点与割边
定义
连通分量:在一张无向图中的极大连通子图即为该图的连通分量。
割点:去掉这个点后,这张无向图的连通分量数量增加,则这个点称为这个图的割点。
割边:去掉这条边后,这张无向图的连通分量数量增加,则这条边称为这个图的割边。
求割点
主要思路
以下提到的有关树的内容,全部指的是对连通分量做 DFS 得到的 DFS 生成树上的内容。
我们对一个连通分量做一次 DFS,可以得到一棵搜索树。这里引入两个定理:
-
如果这棵 DFS 生成树的根节点至少有两个儿子节点,那么这个根节点是割点。
-
这棵 DFS 生成树中的非根节点的一个儿子节点不能不通过它们之间的连边回到这个点的祖先,那么这个点就是割点。
先看定理
这个很好理解,如果这个根节点不是割点,说明根节点只有一个儿子,因为其他点都可以在不经过根节点的情况下两两到达。看图:

图中黑色边为以
否则将这个节点删掉,一定会使连通分量的数量增加,因为有节点必须通过根节点才能到达别的节点。如图:
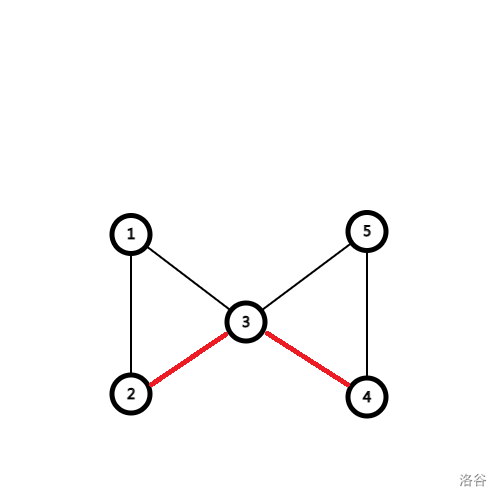 、
、
黑色边是以
我们再看定理
如果删掉这个点,连通分量数量变多,说明有点不再与其他点连通,即没有返祖边连回这个点的祖先。否则一定可以通过这条返祖边连回这个点的祖先,那么连通分量数量也不会增加。

在这个图中,搜索树以
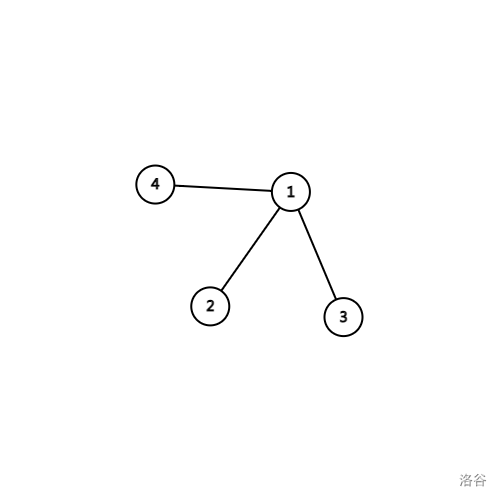
可以看到,连通分量数量并没有增加。因为节点
那么要如何实现呢?我们可以在 dfs 时记录一个点的
那么如何更新
-
在遍历完
-
如果
那么判断割点也很好判断了,根据定理
举个例子:
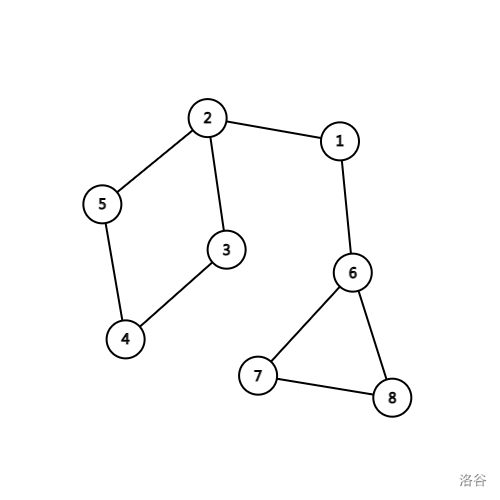
对于上图,我们从
遍历节点
遍历节点
遍历节点
遍历节点
遍历节点
发现节点
回溯至节点
回溯至节点
回溯至节点
回溯至节点
遍历节点
遍历节点
遍历节点
发现节点
回溯至节点
回溯至节点
回溯至节点
由于根节点
所以这张图上的割点为
code
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,dfn[maxn],low[maxn],f[maxn],cnt;
vector<int> G[maxn];
void dfs(int cur,int u,int fa){
dfn[u]=low[u]=++cnt;
int sum=0;
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
if(!dfn[v]){
sum++;
dfs(cur,v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&u!=cur){
f[u]=1;
}
}
else if(dfn[v]<dfn[u]&&v!=fa){
low[u]=min(low[u],dfn[v]);
}
}
if(u==cur&&sum>=2){
f[cur]=1;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
dfs(i,i,-1);
}
}
int ans=0;
for(int i=1;i<=n;i++){
if(f[i]) ans++;
}
cout<<ans<<endl;
for(int i=1;i<=n;i++){
if(f[i]) cout<<i<<" ";
}
return 0;
}
求割边
求割边,只要将求割点的条件从
为什么?
考虑何时
当从
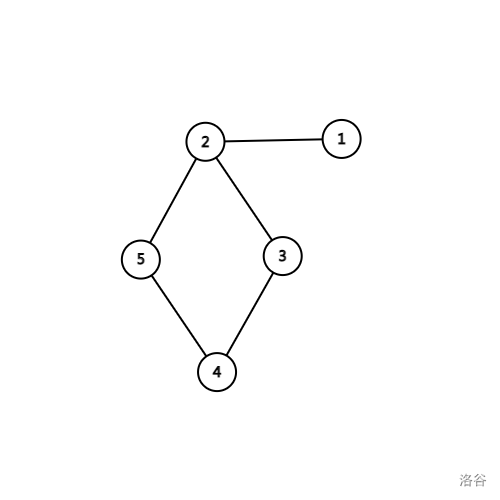
图中节点
但是我们注意到
双连通分量
定义
点双连通分量:如果一个连通分量中不存在割点,则这个连通分量称为点双连通分量。
边双连通分量:如果一个连通分量中不存在割边,则这个连通分量称为边双连通分量。
求点双连通分量
问题:在一张无向图
这里有一个性质:割点会把一个连通分量分为若干个点双。
所以我们在求解割点的时候,使用栈来记录已经遍历过的边。当我们找到割点的时候,我们已经完成了对一个点双的遍历,所以此时栈中的元素就是一个点双。
为什么放入栈中的不是点,是边?
因为一条边只属于一个点双,而一个点可以属于多个点双,当这个点被弹出,就意味着这个点不能属于其他点双,所以存点会错。
生成树问题
生成树的定义
对于一张图
最小生成树
问对于一张图
Kruskal 算法
考虑将所有边按照边权从小到大排序,然后从小到大选择。
但是有个问题:如果我们选择的边连接的两个节点已经联通怎么办?
很简单,不选这个节点就好了。
连通性考虑并查集维护即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
struct edge{
int u,v,w;
bool operator <(edge x){
return w<x.w;
}
}a[maxn];
int n,m,f[maxn],cnt,sum;
int find(int x){
if(f[x]!=x){
f[x]=find(f[x]);
}
return f[x];
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>a[i].u>>a[i].v>>a[i].w;
}
for(int i=1;i<=n;i++){
f[i]=i;
}
sort(a+1,a+m+1);
for(int i=1;i<=m;i++){
int fu=find(a[i].u),fv=find(a[i].v);
if(fu!=fv){
f[fu]=fv;
sum+=a[i].w;
cnt++;
if(cnt==n-1){
break;
}
}
}
int x=find(1);
for(int i=2;i<=n;i++){
if(find(i)!=x){
cout<<"orz"<<endl;
return 0;
}
}
cout<<sum<<endl;
return 0;
}
Prim 算法
从任意一个结点开始,将结点分成两类:已加入的,未加入的。
每次从未加入的结点中,找一个与已加入的结点之间边权最小值最小的结点。
然后将这个结点加入,并连上那条边权最小的边。
重复
拓扑排序
定义
在一张
满足上述条件的即为一个合法的序列。
过程
我们开一个队列,然后用一个数组记录入度。
一开始,我们将入度为
然后不断弹出队首
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cvi>>u>>v;
addedge(u,v);
in[v]++;
}
queue<int> q;
for(int i=1;i<=n;i++){
if(!in[i]){
q.push(i);
}
}
while(q.size()){
int u=q.front();
q.pop();
a[u]=++topo;//a[u]即为 u 的一个合法拓扑序
for(int v:G[u]){
in[v]--;
if(!in[v]){
q.push(v);
}
}
}
例题
[例题1 旅行计划]
拓扑排序常常与 dp 搭配食用。
本题是 DAG 上最长链的简单问题。
对于原图做一遍拓扑排序,然后令
然后在原图上按拓扑序 dp,对于每一条进入
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,dp[maxn],in[maxn],cnt,a[maxn];
vector<int> G[maxn],Gx[maxn];
queue<int> q;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v;
G[u].push_back(v);
Gx[v].push_back(u);
in[v]++;
}
for(int i=1;i<=n;i++){
dp[i]=1;
if(in[i]==0){
q.push(i);
}
}
while(q.size()){
int t=q.front();
q.pop();
a[++cnt]=t;
for(int i=0;i<G[t].size();i++){
int v=G[t][i];
in[v]--;
if(in[v]==0){
q.push(v);
}
}
}
for(int i=1;i<=n;i++){
int u=a[i];
for(int j=0;j<G[u].size();j++){
int v=G[u][j];
dp[v]=max(dp[v],dp[u]+1);
}
}
for(int i=1;i<=n;i++){
cout<<dp[i]<<endl;
}
return 0;
}
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,dp[maxn],in[maxn],cnt,a[maxn];
vector<int> G[maxn],Gx[maxn];
queue<int> q;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v;
G[u].push_back(v);
Gx[v].push_back(u);
in[v]++;
}
for(int i=1;i<=n;i++){
dp[i]=1;
if(in[i]==0){
q.push(i);
}
}
while(q.size()){
int t=q.front();
q.pop();
a[++cnt]=t;
for(int i=0;i<G[t].size();i++){
int v=G[t][i];
in[v]--;
if(in[v]==0){
q.push(v);
}
}
}
for(int i=1;i<=n;i++){
int u=a[i];
for(int j=0;j<G[u].size();j++){
int v=G[u][j];
dp[v]=max(dp[v],dp[u]+1);
}
}
for(int i=1;i<=n;i++){
cout<<dp[i]<<endl;
}
return 0;
}
例题2 因果倒置
本题是拓扑序的很新的应用。
solution
我们先不看所有的无向边,对这个有向图做一遍拓扑排序。
这个时候若我们发现有环,就可以直接 NO 退出。
否则一定有解。
我们考虑一个 DAG 的拓扑序的定义:若
所以我们容易得到,对于每一条无向边,直接考虑这条边连着的两个点哪个拓扑序小,从小的点往大的点连边,就一定不会出现环(因为这样连边原 DAG 的拓扑序不会改变,自然还是一个 DAG)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+10;
int n,m,k,a[maxn],in[maxn],cnt;
vector<int> G[maxn];
queue<int> q;
signed main(){
freopen("cause.in","r",stdin);
freopen("cause.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
G[u].push_back(v);
in[v]++;
}
for(int i=1;i<=n;i++){
if(!in[i]){
q.push(i);
}
}
while(q.size()){
int u=q.front();
q.pop();
a[u]=++cnt;
// cout<<u<<endl;
for(int i=0;i<G[u].size();i++){
int v=G[u][i];
in[v]--;
if(!in[v]){
q.push(v);
}
}
}
if(cnt!=n){
cout<<"NO"<<endl;
return 0;
}
cout<<"YES"<<endl;
cin>>k;
for(int i=1;i<=k;i++){
int u,v;
cin>>u>>v;
if(a[u]>a[v]){
swap(u,v);
}
cout<<u<<" "<<v<<endl;
}
return 0;
}
欧拉路
一些定义
-
欧拉回路:恰好经过每条边一次的回路。
-
欧拉图:存在欧拉回路的图。
-
欧拉通路:恰好经过每条边一次的一条路径。
-
半欧拉图:仅存在欧拉回路的图。
欧拉图的判定
-
一个无向图
-
一个有向图
-
一个无向图
算法流程为从一条回路开始,每次任取一条目前回路中的点,将其替换为一条简单回路,以此寻找到一条欧拉回路。如果从路开始的话,就可以寻找到一条欧拉路。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现