动态规划合集
关于dp
动态规划(简称dp)是一类思想,主要通过分段求解的方式来解决一些决策类问题。
dp所能解决的问题
能用dp解决的问题需要满足三个条件:
- 最优子结构
- 子问题重叠
- 无后效性
最优子结构
- 证明问题最优解的第一个组成部分是做出一个选择;
- 对于一个给定问题,在其可能的第一步选择中,假定你已经知道哪种选择才会得到最优解。你现在并不关心这种选择具体是如何得到的,只是假定已经知道了这种选择;
- 给定可获得的最优解的选择后,确定这次选择会产生哪些子问题,以及如何最好地刻画子问题空间;
- 证明作为构成原问题最优解的组成部分,每个子问题的解就是它本身的最优解。方法是反证法,考虑加入某个子问题的解不是其自身的最优解,那么就可以从原问题的解中用该子问题的最优解替换掉当前的非最优解,从而得到原问题的一个更优的解,从而与原问题最优解的假设矛盾。
子问题重叠
我们可以使用记忆化的方法去记录每一个子问题的解,避免重复解答某一个(或多个)子问题,进而降低整个算法的时间复杂度。
无后效性
你当前一步所做的决策不会对后面造成影响(打个比方,数字三角形,你不能走了这一步,你右边的数全都垮了)。
dp的三个要点:
- 状态
- 状态转移方程
- 边界值与求解顺序
数字三角形问题
有一个数字三角形,你需要从三角形的顶部走到底部,每次可以从这个数字下面的两个数字之间选择一个走,问经过的数字之和最大是多少。
首先肯定会想到贪心:每次往更大的那一边走。
但是这个做法显然是错的,看这个例子:
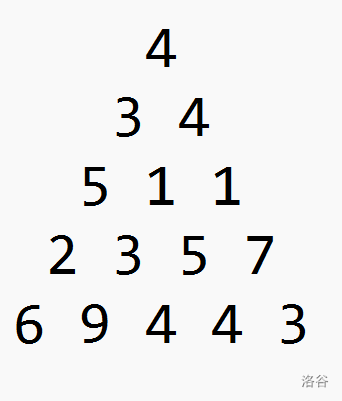
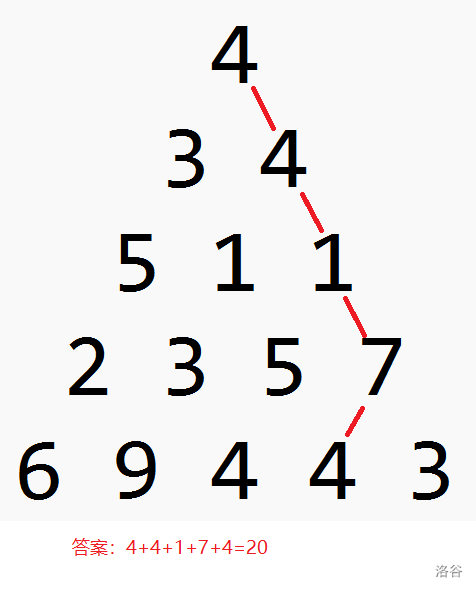
若按照贪心做法,则路径如下:
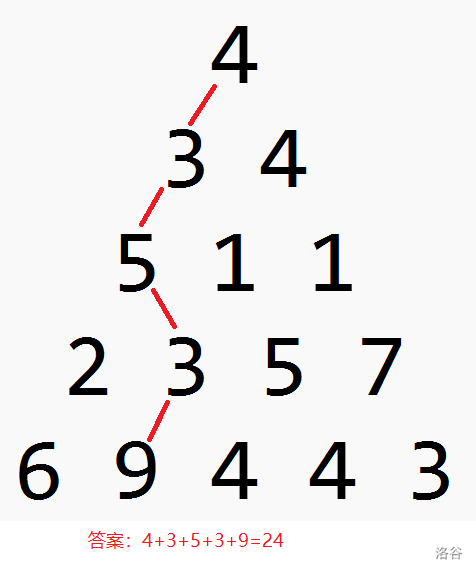
实际最优路径为:
这时我们就会采用动态规划的思想来解决这个问题。
我们令 \(dp_{i,j}\) 为从顶部走到 \((i,j)\) 所经过的最长路径,\(a_{i,j}\) 为第 \(i\) 行第 \(j\) 列的数。
现在,我们思考如何得到这个 \(dp_{i,j}\)。
对于每个数字,我们可以从它上面的两个数(即 \(a_{i-1,j}\) 和 \(a_{i-1,j-1}\))走来,也就是说我们可以选择 \(dp_{i-1,j}\) 和 \(dp_{i-1,j-1}\) 大的那一个来走到这个点,此时 \(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-1})+a_{i,j}\)。
那么我们就完成了这一题。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1000+10;
int f[maxn][maxn],a[maxn][maxn],n;
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>a[i][j];
f[i][j]=max(f[i-1][j],f[i-1][j-1])+a[i][j];
}
}
int ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,f[n][i]);
}
cout<<ans;
return 0;
}
背包dp
部分背包
这个好像不是dp吧
给出物品的重量 \(w_i\) 和价值 \(v_i\),每个物品可以被分割,分割后的性价比不变,问最大价值。
这什么水题啊这题太简单了,直接一个 \(\mathsf{sort}\) 然后贪心就完事了。
代码就不写了,懒得写了太简单了。
下一个·
0-1背包
给出物品的重量 \(w_i\) 和价值 \(v_i\),每个物品只能选一次,问最大价值。
我们设 \(dp_{i,j}\) 为只考虑前 \(i\) 个物品,且容量为 \(j\) 时的最优解。
每一种物品有选与不选两种状态。如果选,那么不难想到 \(dp_{i,j}=dp_{i-1,j-w_i}+v_i\),因为之前是没考虑这个物品的,所以是 \(i-1\);\(j\) 代表的是容量,所以是 \(j-w_i\)。
那么如果不放,总容量不会减少,价值也不会增多,所以当选择不放时,\(dp_{i,j}=dp_{i-1,j}\)。
综合一下,就有 \(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-w_i}+v_i)\)。
for(int i=1;i<=n;i++){//枚举所有物品数量
for(int j=1;j<=c;j--){//枚举所有容量的情况
dp[i][j]=dp[i-1][j];
if(j>=w[i]) dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
}
}
注意循环顺序即可。
完全背包
给出物品的重量 \(w_i\) 和价值 \(v_i\),每个物品可以选无数次,问最大价值。
还是一样,我们设 \(dp_{i,j}\) 为只考虑前 \(i\) 个物品,且容量为 \(j\) 时的最优解。
只是在完全背包问题中,每个物品都可以被选无数次。
所以我们可以在内层再套一层循环 \(k\),用来枚举选择物品的数量。
当然,\(k\) 不可以超过 \(\lfloor \dfrac{w_i}{j} \rfloor\)。否则会数组越界。
因为有 \(k\) 个物品,所以我们的状态转移方程就变成了 \(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-w_i \times k}+v_i \times k)\)。
代码如下:
for(int i=1;i<=n;i++){//枚举所有物品数量
for(int j=0;j<=w[i];j++){//枚举所有容量的情况
for(int k=0;k<=w[i]/j;k++){//枚举所有物品数量的情况
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]*k]+v[i]*k);
}
}
}
如果能熟记 01 背包的话,相信完全背包也没问题。
多重背包
给出物品的重量 \(w_i\) 、价值 \(v_i\) 以及可以选择的次数 \(m_i\)(即每个物品最多选 \(m_i\) 次),问最大价值。
在这里,我们很容易想到将最内层的 \(k\) 循环的条件改一下,于是就有:
for(int i=1;i<=n;i++){//枚举所有物品数量
for(int j=0;j<=c;j++){//枚举所有容量的情况
for(int k=0;k<=m[i];k++){//枚举所有物品数量的情况
if(j>=w[i]*k) dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]*k]+v[i]*k);
}
}
}
注意,在改了内层循环之后要加一个 \(\mathsf{if}\),防止数组越界。
这里同样可以使用滚动数组进行优化。
代码就不展示了。
混合背包
给出物品的重量 \(w_i\) 和价值 \(v_i\) ,然后告诉你哪些是可以选无数次,哪些只能被选 \(m_i\) 次,问最大价值。
这种问题乍一看很吓人,实际上只要用 \(\mathsf{if}\) 判断一下,然后直接套公式。
这里给出伪代码。
for(枚举考虑前 i 个物品){
if(是01背包){
套用01背包状态转移方程;
}
if(是完全背包){
套用完全背包状态转移方程;
}
if(是多重背包){
套用多重背包状态转移方程;
}
}
分组背包
题面通天之分组背包
先翻到上面复习一下01背包
这一题就是在01背包的基础上增加了一个求组数。
我们只需要对于每一组都跑一次01背包就好了。
核心代码如下:
for(int i=1;i<=n;i++)//枚举小组
for(int j=c;j>=1;j--)//枚举容量
for(int z=0;z<k[i];z++)//枚举物品
if(w[i][z]<=j)
dp[j]=max(dp[j],dp[j-w[i][z]]+v[i][z]);
背包问题的滚动数组优化
这里以 01 背包的优化为例。
注意到我们求出一个 \(dp_{i,j}\) 只需要用到上一行比它靠前位置的信息。
于是我们便可以倒着循环,循环中 \(\ge j\) 为本行信息,\(<j\) 为上一行信息,这样可以保证答案一定从上一行转移来。
for(int i=1;i<=n;i++){
for(int j=c;j>=w[i];j++){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
区间dp
区间 dp,顾名思义,就是在区间上做 dp
先用一个例题引入:
石子合并(弱化版)
我们可以令 \(f_{i,j}\) 为合并 \([i,j]\) 这个区间所需的最小代价。
考虑这个 \([i,j]\) 可以怎样得到:
-
将 \([i,i]\) 与 \([i+1,j]\) 合并得到;
-
将 \([i,i+1]\) 与 \([i+2,j]\) 合并得到;
-
将 \([i,i+2]\) 与 \([i+3,j]\) 合并得到;
-
\(\dots\)
-
将 \([i,j-1]\) 与 \([j,j]\) 合并得到。
代价均为 \(\sum\limits_{x=i}\limits^{j} a_x\)。
所以这个时候我们可以枚举一个“断点” \(k\),取所有 \(f_{i,k}+f_{k+1,j}\) 之间的 \(\min\) 即可。于是得到转移方程 \(f_{i,j}=\min\limits_{k=1}\limits^{j-1} f_{i,k}+f_{k+1,j}+\sum\limits_{x=i}\limits^{j} a_x\)。
这里还有一个问题:区间 dp 的转移顺序是怎么样的?
如果直接像下面这样 dp:
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=i;k<j;k++){
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
}
}
}
则会出现问题:在转移到某个区间时,有可能这个区间所包含的所有子区间的 \(f\) 还没计算。
所以区间 dp 的转移顺序应该是从小区间转移到大区间的。
此时我们枚举区间长度 \(L\) 和左端点 \(i\) 进行转移即可。
for(int L=1;L<n;L++){
for(int i=1,j=i+L;j<=n;i++,j++){
for(int k=i;k<j;k++){
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
}
}
}
答案即为 \(f_{1,n}\)。
区间 dp 衍生出的环形 dp:石子合并
考虑到这个序列变成了一个环,就不好 dp 了。
此时,我们采用一种叫“断环为链”的思想,见下图:
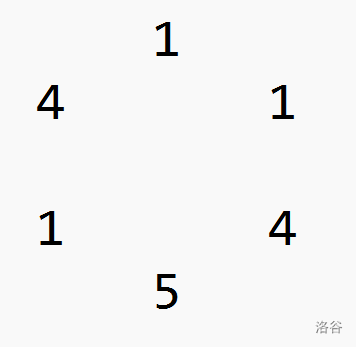
我们可以将这个环断为序列 \(1,1,4,5,1,4,1,1,4,5,1,4\),此时序列上长度为 \(6\) 的每一个区间刚好对应环上的每一个长度为 \(6\) 的区间。
此时进行区间 dp,统计每个长度为 \(6\) 的区间的答案即可。
for(int L=2;L<=n;L++){
for(int i=1,j=i+L-1;j<=n*2;i++,j++){
f1[i][j]=0x7f7f7f7f;
for(int k=i;k<j;k++){
f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+1][j]+(sum[j]-sum[i-1]));
f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+1][j]+(sum[j]-sum[i-1]));
}
// cout<<i<<" "<<j<<" "<<f1[i][j]<<" "<<f2[i][j]<<endl;
}
}
int ans1=0x7f7f7f7f,ans2=0;
for(int i=1,j=n;j<=2*n;i++,j++){
ans1=min(ans1,f1[i][j]);
ans2=max(ans2,f2[i][j]);
}
向两端扩展+分类讨论的区间 dp:回文子串
令 \(f_{i,j}\) 为 \([i,j]\) 变为回文串所需的最少添加字符数。
先考虑如下问题:
如果我要将 qingzhengqwq 变为回文串,由于两端的字符相等,所以直接考虑 ingzhengqw 的代价即可。
如果我要将 qingzheng 变为回文串,由于两端的字符不等,所以考虑在字符串之前加上一个 g 或在字符串末尾加上一个 q。此时再考虑 ingzheng 和 qingzhen 中代价较小的哪一个即可。
由此,我们可以得到:
-
若 \(s_i=s_j\),那么 \(f_{i,j}=f_{i+1,j-1}\),由于现在已经将 \([i+1,j-1]\) 花费 \(f_{i+1,j-1}\) 的代价变为了回文串,所以再在两边套上两个相同的字符依然是回文串,不需要花费额外代价;
-
否则我们考虑 \(f_{i+1,j}\) 和 \(f_{i,j-1}\) 哪个更小,若 \(f_{i+1,j}\) 更小,则我们可以在 \([i,j]\) 末尾添加一个 \(s_i\) 使得 \([i,j]\) 变为回文串,反之亦然。
所以我们得出了转移方程:
\(f_{i,j}=\min(f_{i+1,j},f_{i,j-1})+1\);
\(f_{i,j}=\min(f_{i,j},f_{i+1,j-1})\),须满足 \(s_i=s_j\)。
for(int l=0;l<len;l++){
for(int i=1,j=i+l;j<=len;i++,j++){
dp[i][j]=min(dp[i+1][j]+1,dp[i][j-1]+1);
if(s[i]==s[j]){
dp[i][j]=min(dp[i][j],dp[i+1][j-1]);
}
}
}
状压 dp
状压 dp 本质上是将一个状态压缩为一个整数(通常为二进制)来达到优化转移的目的。
使用状压 dp 需要很熟悉位运算。
先放例题:
例1 取数游戏
这题虽然可以 dfs 过掉,但还是将它归为状压 dp 的例题之一。
令 \(f_{i,j}\) 为考虑到第 \(i\) 行,第 \(i\) 行状态为 \(j\) 的取数最大值。
枚举所有状态(\(N\) 最多只有 \(6\),所以状态总数只有 \(2^6\)),然后进行转移。
由于选的数在单行内的限制表现为不能左右相邻,所以状态 \(j\) 需要满足 j&(j<<1)==0 且 j&(j>>1)==0。
然后枚举上一行的状态转移。
上一行的状态 \(k\) 除了需要满足上述条件外,由于选数不能八相邻,所以需要额外满足 j&k==0 且 j&(k<<1)==0 且 j&(k>>1)==0。
此外,我们还需要一个函数来计算第 \(i\) 行若状态为 \(j\),选出的数总和是多少,记为 \(getsum(i,j)\)。
转移方程就是 \(f_{i,j}=f_{i-1,k}+getsum(i,j)\)。
#include<bits/stdc++.h>
using namespace std;
const int maxn=6+10;
int n,m,a[maxn][maxn],dp[maxn][1<<6];
int getsum(int x,int num){
int cnt=m,sum=0;
while(num){
sum+=a[x][cnt--]*(num&1);
num>>=1;
}
return sum;
}
void debug(int x){
stack<int> st;
while(x){
st.push(x&1);
x>>=1;
}
while(st.size()){
cout<<st.top();
st.pop();
}
cout<<endl;
}
bool check(int x){
return (!(x&(x<<1))&&!(x&(x>>1)));
}
void solve(){
memset(dp,0,sizeof dp);
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
int s=1<<m;
for(int i=0;i<s;i++){
if(check(i)){
dp[1][i]=getsum(1,i);
}
}
for(int i=2;i<=n;i++){
for(int j=0;j<s;j++){
if(check(j)){
for(int k=0;k<s;k++){
// cout<<"j:";debug(j);
// cout<<"k:";debug(k);
if(check(k)&&(!(j&k))&&!(j&(k<<1))&&!(j&(k>>1))){
// cout<<"in"<<endl;
dp[i][j]=max(dp[i][j],dp[i-1][k]+getsum(i,j));
}
}
}
}
}
int ans=0;
for(int i=0;i<s;i++){
if(check(i)){
ans=max(ans,dp[n][i]);
}
}
cout<<ans<<endl;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t;
cin>>t;
while(t--) solve();
return 0;
}
其实状压 dp 还挺抽象的。
之后的题目基本都是考虑到几行,然后状态为啥啥啥这种了。

