数据结构合集
并查集
普通并查集
先看一个问题:
P1551 亲戚
规定:\(x\) 和 \(y\) 是亲戚,\(y\) 和 \(z\) 是亲戚,那么 \(x\) 和 \(z\) 也是亲戚。如果 \(x\),\(y\) 是亲戚,那么 \(x\) 的亲戚都是 \(y\) 的亲戚,\(y\) 的亲戚也都是 \(x\) 的亲戚。现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
思路
我们令 \(f_i\) 为节点 \(i\) 的父亲。一开始,\(f_i=i\),因为最开始 \(i\) 的父亲不是任何人。
接下来开始维护“合并”操作。对于一条“\(x\) 是 \(y\) 的亲戚”的一条信息,不妨设 \(x\) 是 \(y\) 的父亲,此时我们爬树找到 \(y\) 的“祖先”(可以发现,并查集建完之后是一个森林,就相当于找到节点 \(y\) 所在的树的根节点),记为 \(fy\),将 \(f_{fy}\) 设为 \(x\) 所在树的根节点即可。
int find(int x){//寻找 x 所在树的根节点
if(f[x]==x){
return f[x];
}
else{
return find(f[x]);
}
}
int merge(int x,int y){//将 y 所在的集合(树)合并到 x 所在的集合(树)
int fx=find(x),fy=find(y);
f[fy]=fx;
}
那么“查询” \(x\) 和 \(y\) 是否在同一个集合内。我们不断从节点 \(x\) 和节点 \(y\) 向上爬树,如果他们的祖先相同,那么必定在一棵树内,即具有亲戚关系,否则就不具有亲戚关系。
bool query(int x,int y){//查询 x 与 y 是否在一个集合
if(find(x)==find(y)){
return 1;
}
return 1;
}
并查集的路径压缩优化
为什么要路径压缩?
考虑并查集的这种情况:

这样的话,每次查询操作的时间复杂度就会退化为线性。
那么怎么进行路径压缩?
我们每次查询的时候直接把查询一路上的所有点的 \(f\) 值直接设为最终查询的结果即可。
我们对上图进行路径压缩:
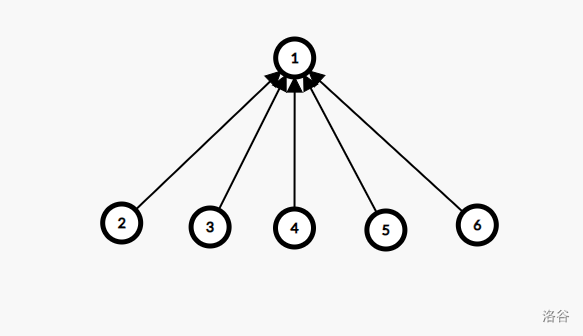
代码如下:
int find(int x){
if(f[x]!=x){
f[x]=find(f[x]);//路径压缩,即将每个访问路径上的点的父亲都直接设为这棵树的根节点
}
return f[x];
}

优化了整整 \(100ms\)。
此外,普通并查集还被用于 kruskal 最小生成树的算法中。
带权并查集
我们在每个点与父亲之间的连边上定义一个权值,并在路径压缩时做维护,就能够解决更多的问题。
例题1 食物链
我们令边权为 \(0\) 的是同一种动物,\(1\) 为捕食关系,\(2\) 为被捕食关系。
然后我们发现在 \(\bmod 3\) 意义下,\(1+2=0\)(\(A\) 捕食 \(B\),\(B\) 被 \(C\) 捕食,即 \(A\) 与 \(C\) 是同种动物)等式子成立,所以用带权并查集维护即可。
树状数组
普通树状数组
这个玩意大概长成这个样子:
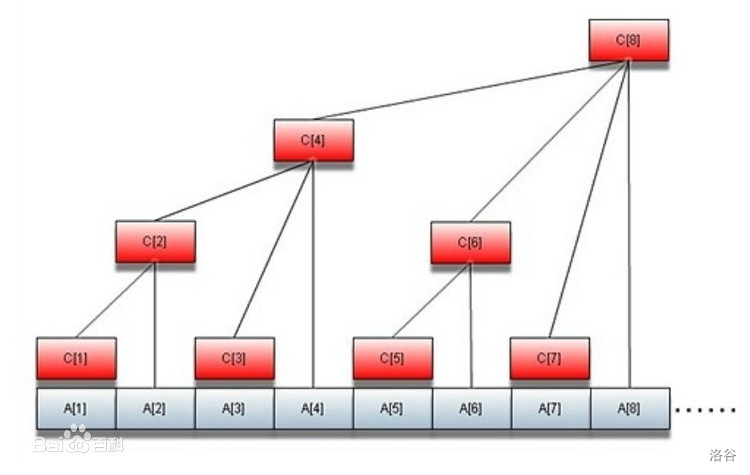
(这里用了百度的图片)
其实它就是一个特殊的前缀和数组。
单点修改
仔细观察红色框内与灰色框的关系:
\(c_1=a_1\)
\(c_2=a_1+a_2\)
\(c_3=a_3\)
\(c_4=a_1+a_2+a_3+a_4\)
\(c_5=a_5\)
\(c_6=a_5+a_6\)
\(c_7=a_7\)
\(c_8=a_5+a_6+a_7+a_8\)
于是我们可以发现以下规律:
\(c_i=a_{i-2^k+1}+a_{i-2^k+2}+\dots+a_i\)
那么我们找出 \(i\) 的二进制下最低位的 \(1\) ,然后一步步往上更新便可实现 \(O(\log n)\) 单点修改。
那么问题来了,怎么获取最低位的 \(1\)?
这时候就要引入 \(lowbit\) 函数了。原理如下:
先假设该数最低位的 \(1\) 在第 \(k\) 位上,则按位取反的二进制的第 \(k\) 位为 \(0\),\(0\) 到 \(k-1\) 位全部为1。由于进位,\(0\) 到 \(k-1\) 位全部为 \(0\),第 \(k\) 位为 \(1\),剩下的数位仍然和原来相反。那么 x&(-x) 自然就只剩下最低位的 \(1\) 以及它后面的 \(0\) 构成的数值了。
知道了以上知识以后,便可以写出修改函数:
void add(int x,ll y){//在位置x的数加上y
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=y;
}
}
那么上面那个公式可以这么写:
\(c_i=\sum\limits^i\limits_{j=i-lowbit(i)+1} a_i\)
那么在跑代码的过程中,科技数据结构内部发生了啥?这里用 \(add(5,1)\) 来举例:
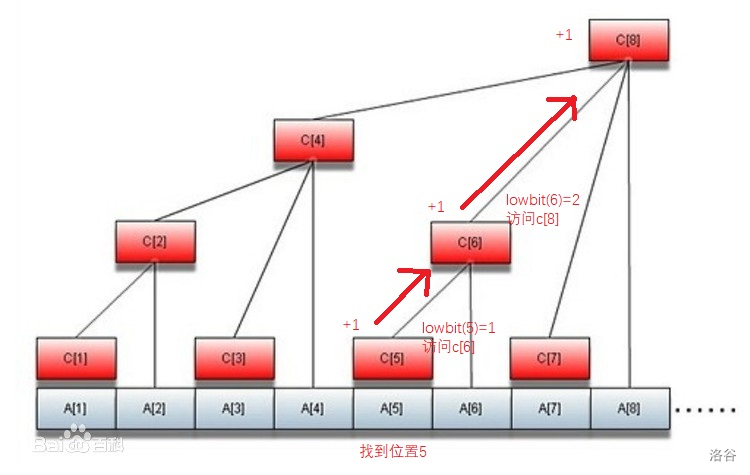
可以看到,我们要想单点修改 \(a[5]\),则需修改所有包含 \(a[5]\) 的区间值,在本例中即为 \(c[5],c[6],c[8]\)。
区间查询
利用前缀和思想,我们可以知道求 \(a_x\) 到 \(a_y\) 的和就是求 \(a_1\) 到 \(a_y\) 的和减去 \(a_1\) 到 \(a_{x-1}\) 的和。
那么把问题拆开来看,如何求 \(a_1\) 到 \(a_x\) 的和?
我们可以先将 \(c_i\) 加入答案,此时我们的问题变成了求 \(a_1\) 到 \(a_i-lowbit(i)\) 的和。
那么我们接下来可以将 \(c_{i-lowbit(i)}\) 加入答案。
不断重复以上操作,直到 \(i\) 变为 \(0\)。那么此时我们已经得到答案。
代码如下:
ll search(int x,int y){//查询x到y的和
int sum1=0,sum2=0;
for(int i=x-1;i;i-=lowbit(i)){
sum1+=c[i];
}
for(int i=y;i;i-=lowbit(i)){
sum2+=c[i];
}
return sum2-sum1;
}
我们还是来看看树状数组内部发生的事情,这里拿查询区间 \([4,6]\) 举例。
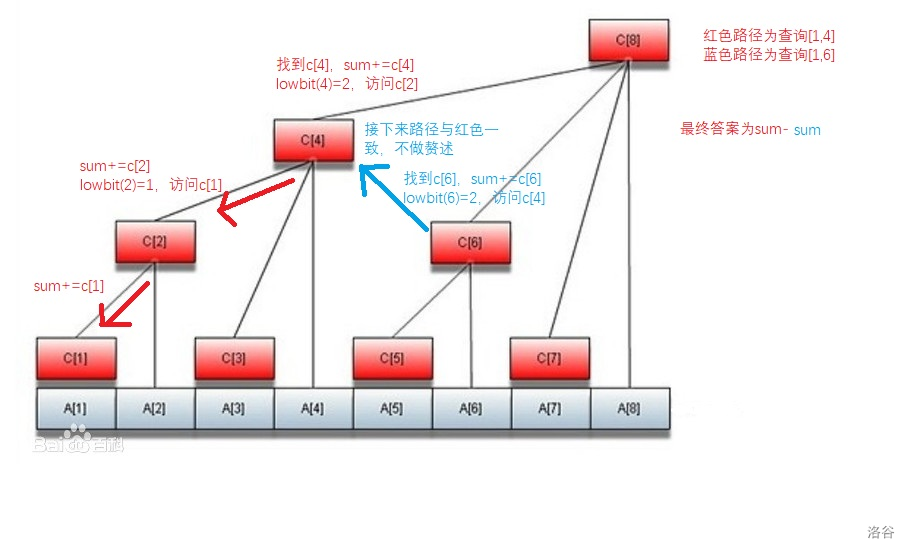
(上图的答案计算写反了,应该是 \(\color{skyblue}{sum}-\color{red}{sum}\))
可以看到每一步中,都把 \(x\) 变成了 \(lowbit(x)\),结合 \(lowbit\) 函数的概念,相当于不断去掉 \(x\) 二进制中最低位的那个 \(1\)。由于 \(i\) 的二进制表示位数不超过 \(\log i\),所以单点查询复杂度为 \(O(\log n)\)。
那么普通树状数组的模板就打好了,代码:
#include <bits/stdc++.h>
#define ll long long
#define lowbit(x) ((x)&(-x))
using namespace std;
int n,m;
ll a[500001],c[500001];
void add(int x,ll k){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=k;
}
}
ll search(int x,int y){
int sum1=0,sum2=0;
for(int i=x-1;i;i-=lowbit(i)){
sum1+=c[i];
}
for(int i=y;i;i-=lowbit(i)){
sum2+=c[i];
}
return sum2-sum1;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
add(i,a[i]);
}
for(int i=1;i<=m;i++){
int op;
scanf("%d",&op);
if(op==1){
int x;
ll k;
scanf("%d%lld",&x,&k);
add(x,k);
}
else{
int x,y;
scanf("%d%d",&x,&y);
printf("%lld\n",search(x,y));
}
}
return 0;
}
树状数组求逆序对
我们倒着扫一遍要求逆序对的序列 \(a\),并在扫的时候先将把 \(a_i\) 位置 \(+1\),然后答案加上当前 \([1,a_i)\) 的和。
为什么要这么做?
考虑逆序对的定义:\(a_i>a_j\) 且 \(i<j\)。
这个树状数组 \(c_i\) 维护的是数 \(i\) 目前的出现次数。
我们在扫数的时候,就是在统计 \(a_i\) 作为较大数贡献的逆序对数量,而目前加入树状数组中的数全部满足条件 \(2\)(\(i<j\)),所以我们直接统计 \([1,a_i)\) 的和(即目前比这个数小的数的数量)就是 \(a_i\) 所贡献的逆序对数量。
#include<bits/stdc++.h>=
#define int long long
using namespace std;
int n,a[500001],b[500001],c[500001],ans;
bool cmp(int x,int y){
if(a[x]==a[y]) return x<y;
return a[x]<a[y];
}
void update(int x,int y){
for(int i=x;i<=n;i+=(i&(-i))){
c[i]+=y;
}
}
int sum(int x){
int ans=0;
for(int i=x;i;i-=(i&(-i))){
ans+=c[i];
}
return ans;
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
b[i]=i;
}
sort(b+1,b+n+1,cmp);
for(int i=n;i>=1;i--){
ans+=sum(b[i]);
update(b[i],1);
}
cout<<ans;
return 0;
}
树状数组的区间修改、单点查询
如果扫一遍区间去维护,那么单次操作时间 \(O(n \log n)\),甚至不如暴力。
容易想到对原序列作差分,此时区间 \([l,r]\) 的修改变为对差分序列上 \(l\) 和 \(r+1\) 的单点修改,可以直接用树状数组维护。
那么原序列 \(a_x\) 的值就相当于差分序列 \(b\) 上区间 \([1,x]\) 的和,也可以用树状数组维护。
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e5+10;
int n,c[maxn],m;
int lb(int x){
return x&(-x);
}
void update(int x,int v){
for(int i=x;i<=n;i+=lb(i)){
c[i]+=v;
}
}
int query(int x){
int sum=0;
for(int i=x;i;i-=lb(i)){
sum+=c[i];
}
return sum;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
int x;
cin>>x;
update(i,x);
update(i+1,-x);
}
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int x,y,k;
cin>>x>>y>>k;
update(x,k);
update(y+1,-k);
}
if(op==2){
int x;
cin>>x;
cout<<query(x)<<endl;
}
}
return 0;
}
树状数组的区间修改、区间查询
如果直接暴力更新或查询,那么单次操作复杂度将会是 \(O(n \log n)\),比暴力还高。
所以还是考虑维护差分数组。
我们现在要求的是一个前缀和,即 \(\sum\limits_{i=1}\limits^x a_i\)。
我们根据差分数组 \(b\) 的定义,有 \(a_i=\sum\limits_{j=1}\limits^i b_j\)。
于是我们就有 \(\sum\limits_{i=1}\limits^x a_i=\sum\limits_{i=1}\limits^{x}\sum\limits_{j=1}\limits^i b_i\)。
发现 \(b_i(i \in [1,x])\) 在这个式子中被计算了 \(x-i+1\) 次,于是有 \(\sum\limits_{i=1}\limits^{x}\sum\limits_{j=1}\limits^i b_i=\sum\limits_{i=1}\limits^x b_i \times (x-i+1)\)。
根据乘法分配律,有 \(\sum\limits_{i=1}\limits^x b_i \times (x-i+1)=\sum\limits_{i=1}\limits^x b_i \times (x+1)-\sum\limits_{i=1}\limits^x b_i \times i\)。
然后我们开两个树状数组分别维护 \(b_i\) 和 \(b_i \times i\) 即可。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+10;
int n,m,c1[maxn],c2[maxn];
int lb(int x){
return x&(-x);
}
void update(int x,int v){
for(int i=x;i<=n;i+=lb(i)){
c1[i]+=v;
c2[i]+=x*v;
}
}
int query(int x){
int ans=0;
for(int i=x;i;i-=lb(i)){
ans+=(x+1)*c1[i]-c2[i];
}
return ans;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++){
int x;
cin>>x;
update(i,x);
update(i+1,-x);
}
for(int i=1;i<=m;i++){
int op;
cin>>op;
if(op==1){
int x,y,k;
cin>>x>>y>>k;
update(x,k);
update(y+1,-k);
}
if(op==2){
int x,y;
cin>>x>>y;
cout<<query(y)-query(x-1)<<endl;
}
}
return 0;
}
二维树状数组
前置芝士:二维前缀和,二维差分
考虑二维差分数组 \(b\) 的定义,不难得到左上角为 \((1,1)\),右下角为 \((x,y)\) 的矩阵的和为 \(\sum\limits_{i=1}\limits^{x}\sum\limits_{j=1}\limits^{y}\sum\limits_{k=1}\limits^{i}\sum\limits_{l=1}\limits^{j} b_{k,l}.\)
于是我们集中注意力,发现每个 \(b_{i,j}\) 的出现次数仍然有规律(\(b_{i,j}\) 出现了 \((x-i+1)\times(y-j+1)\) 次),于是有 \(\sum\limits_{i=1}\limits^{x}\sum\limits_{j=1}\limits^{y}\sum\limits_{k=1}\limits^{i}\sum\limits_{l=1}\limits^{j} b_{k,l}=\sum\limits_{i=1}\limits^{x}\sum\limits_{j=1}\limits^y b_{i,j} \times (x-i+1) \times (y-j+1).\)
括号乘开,得:
\(\sum\limits_{i=1}\limits^{x}\sum\limits_{j=1}\limits^y b_{i,j} \times (x-i+1) \times (y-j+1) = b_{i,j} \times(xy+x+y+1) - b_{i,j} \times i \times (y+1) - b_{i,j} \times j \times (x+1) + b_{i,j} \times i \times j.\)
于是开四个树状数组,分别维护 \(b_{i,j}\),\(b_{i,j} \times i\),\(b_{i,j} \times j\) 和 \(b_{i,j} \times i \times j\) 即可。
#include<bits/stdc++.h>
using namespace std;
const int maxn=2048+10;
int n,m;
char op;
int c1[maxn][maxn],c2[maxn][maxn],c3[maxn][maxn],c4[maxn][maxn];
void update(int x,int y,int puck){
int k=puck;
for(int i=x;i<=n;i+=(i&(-i))){
for(int j=y;j<=m;j+=(j&(-j))){
c1[i][j]+=k;
c2[i][j]+=k*x;
c3[i][j]+=k*y;
c4[i][j]+=k*x*y;
}
}
}
int sum(int x,int y){
int ans=0;
for(int i=x;i;i-=(i&(-i))){
for(int j=y;j;j-=(j&(-j))){
ans+=(x+1)*(y+1)*c1[i][j]-(x+1)*c3[i][j]-(y+1)*c2[i][j]+c4[i][j];
}
}
return ans;
}
int main(){
getchar();getchar();
scanf("%d%d",&n,&m);
while(cin>>op){
if(op=='L'){
int a,b,c,d,k;
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
update(a,b,k);
update(a,d+1,-k),update(c+1,b,-k),update(c+1,d+1,k);
}
else{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
int sum1=sum(c,d),sum2=sum(c,b-1),sum3=sum(a-1,d),sum4=sum(a-1,b-1);
printf("%d\n",sum1-sum2-sum3+sum4);
}
getchar();
}
return 0;
}
线段树
线段树,它是树上的每个节点都用来表示一个区间的一颗树。
对于一颗线段树,其根结点为 \([1,n]\)。如果一个节点表示 \([l,r]\) ,则其左儿子为 \([l,mid]\),右儿子为 \([mid+1,r]\)。
线段树的性质
-
对于一个序列长度是 \(n\) 的序列构造线段树,则这颗线段树有 \(2n-1\) 个节点,高度为 \(logn\)。
-
对于一颗线段树上的非叶子节点,都有两个儿子(换句话说就是要么没有儿子要么有两个儿子)。
证一下第一条性质:
知周所众,线段树一共只有 \(n\) 个叶子结点(分别为 \([1,1],[2,2],[3,3] \dots ,[n,n]\))。然后将没父亲结点的结点两两合并,每次合并会新增加一个结点,并且会减少一个没有父结点的结点。所以,我们需要新建 \(n-1\) 个结点才能使没有父结点的结点数降为 \(1\)(根结点没有父结点)。因此节点数为 \(n+n-1=2n-1\)。
普通线段树
构造
我们都知道,树是递归构造的,线段树也是一样。
所以我们需要写一个函数来构造线段树。
这里使用结点表示法。\(a_{now}.l\) 和 \(a_{now}.r\) 代表结点编号为 \(now\) 维护的区间,\(a_{now}.v\) 代表维护这个区间的信息。
递归边界为 \(l=r\)。
void build(int now,int l,int r){
a[now].l=l;
a[now].r=r;
a[now].v=sum[r]-sum[l-1];
if(l!=r){
build(now*2,l,(l+r)/2);
build(now*2+1,(l+r)/2+1,r);
}
}
我们通过一张图来解释线段树对于 \([1,9]\) 的建树过程。
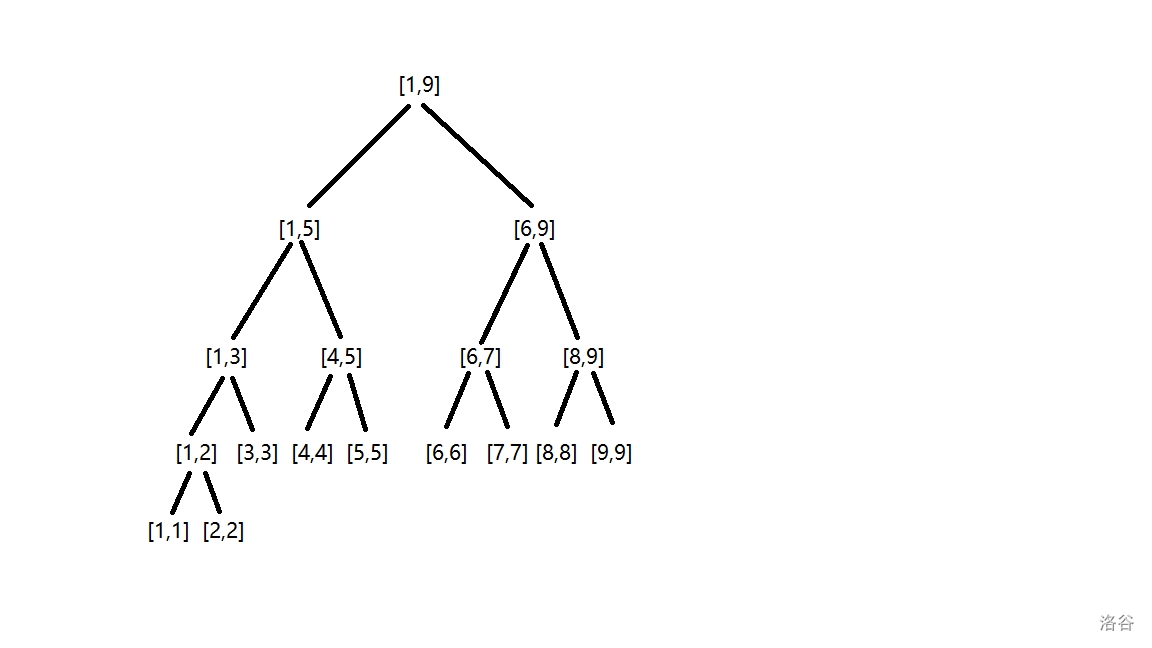
单点查询
单点查询实际上就是定位到线段树的叶子结点。
我们现在假设我们需要定位到 \(x\),那么考虑递归,如果 \(x \le mid\),显然 \([x,x]\) 在右子树中,反之则在左子树中。
int search(int u,int L,int R,int p){
if(L==R){
return a[u].v;
}
else{
int Mid=(L+R)>>1;
if(Mid>=p) return scarch(u<<1,L,Mid,p);
else return scarch((u<<1)|1,M+1,R,p);
}
}
单点修改
进行单点修改,首先也需要定位到这个结点。然后修改完成后,我们需要一路往上更新,这样才能保证线段树的正确性。
int pushup(int u){
a[u].v=a[u<<1].v+a[(u<<1)|1].v;
}
int search(int u,int L,int R,int p,int x){
if(L==R){
a[u].v=x;
}
else{
int Mid=(L+R)>>1;
if(Mid>=p) return scarch(u<<1,L,Mid,p.x);
else return scarch((u<<1)|1,M+1,R,p,x);
}
pushup(u);
}
由于线段树共 \(\log n\) 层,所以单点查询/修改的时间复杂度为 \(O(\log n)\)。
区间查询
假设查询区间为 \([l,r]\),我们从根节点 \([1,n]\) 开始递归查询 \([l,mid]\) 与 \([mid+1,r]\)。此时对递归区间进行分类讨论:
-
当前区间被目标区间完全包含。此时直接返回当前区间的值即可。
-
当前区间与目标区间无交集。此时返回 \(0\)。
-
当前区间没有被目标区间包含且有交。此时递归处理左子树与右子树的和。
举个例子:在以 \([1,9]\) 为根的线段树中查询 \([2,5]\) 时,我们会递归查询到 \([2,2],[3,3],[4,5]\) 这三个区间。这三个区间的和就是答案。如图:
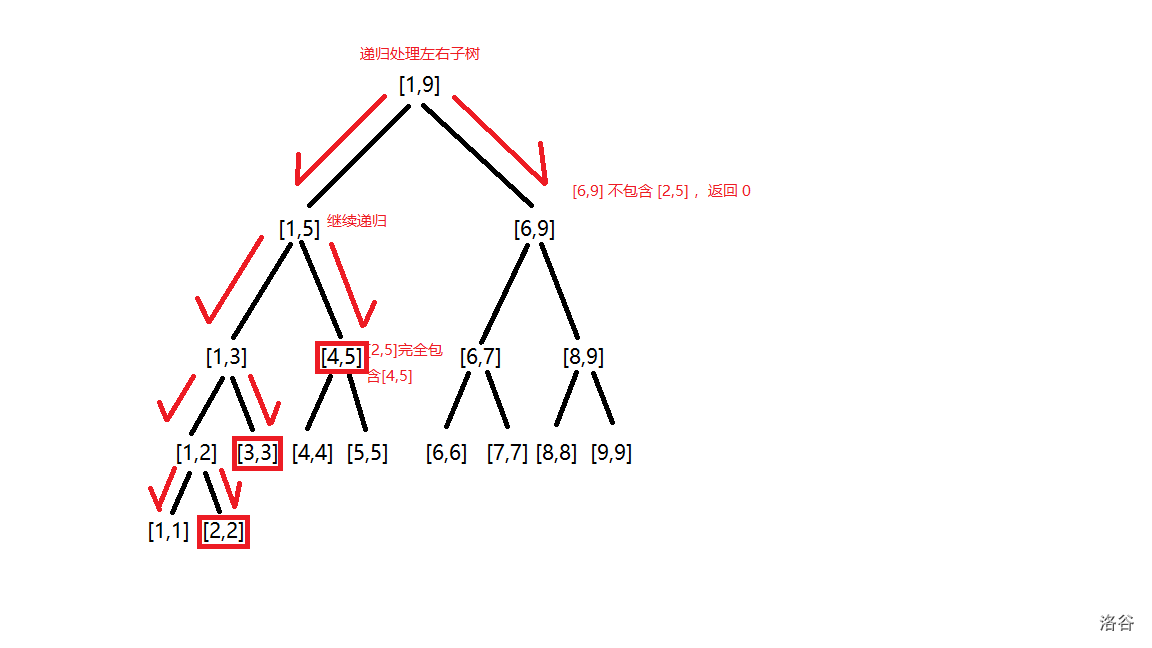
ll query(int u,int L,int R){
if(a[u].tag) pushdown(u);
if(inrange(L,R,a[u].l,a[u].r)){
return a[u].v;
}
else if(!outofrange(L,R,a[u].l,a[u].r)){
return search(ls(u),L,R)+search(rs(u),L,R);
}
else return 0ll;
}
区间修改
需要进行区间修改的时候,我们需要引入一个新东西:懒标记。
对于一个区间 \([l,r]\)来说,我们如果每次都更新区间中的每一个值,那样的话更新的复杂度将会是 \(O(n \log n)\)。
这个复杂度甚至比暴力还高。所以我们引入了懒标记。
懒标记的主要原理是区间修改操作时先对这个区间打上标记,暂时不进行更新,若之后需要用到该节点的信息时再调用 \(\mathsf{pushdown}\) 函数进行更新。
单打标记的复杂度为一个常数。
void pushdown(int u){
int L=a[u].l,R=a[u].r,M=L+R>>1,k=a[u].tag,g=1;
if(L==R) return ;
//if(g==1) printf("%d %d %d %d\n",L,R,M,k);
a[u].tag=0;
a[ls(u)].tag+=k;
a[rs(u)].tag+=k;
a[ls(u)].v+=k*(M-L+1);
a[rs(u)].v+=k*(R-M);
}
void update(int u,int L,int R,ll k){
if(a[u].tag) pushdown(u);
if(inrange(L,R,a[u].l,a[u].r)){
a[u].tag+=k;
a[u].v+=(a[u].r-a[u].l+1)*k;
pushdown(u);
}
else if(!outofrange(L,R,a[u].l,a[u].r)){
update(ls(u),L,R,k);
update(rs(u),L,R,k);
pushup(u);
}
}
单调栈
单调栈解决的问题
很喜欢扶苏的一句话:单调栈的本质是求前缀的后缀最值。
可以理解为在这个数左/右边离他最近的、且比它大/小的值的位置。(在 \(O(n)\) 的复杂度内求出每个数)
这样说有点抽象,看例题。
例题1 [USACO09MAR] Look Up S
借着这个例题说一下单调栈的基本过程。
既然是单调栈,必定要开一个栈。
既然是求右边的比它大的值,我们就从左到右扫。对于每个数,我们扫到这个数的时候需要用这个数更新一些数的答案。
如何更新?
我们不断弹出栈顶,直到栈顶值大于当前值,然后把当前值压入栈中。弹出的元素的答案就是当前的这个元素。不难发现,这个栈中的元素始终单调递减。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,ans[maxn],a[maxn];
stack<int> s;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
while(s.size()&&a[s.top()]<a[i]){
ans[s.top()]=i;
s.pop();
}
s.push(i);
}
for(int i=1;i<=n;i++){
cout<<ans[i]<<endl;
}
return 0;
}
有了单调栈这个工具以后,我们尝试解决一些很新的问题。
例题2 发射站
注意到发出的能量只被两边最近的且比它高的发射站接收,一眼单调栈可以解决。
现在的问题就是如何统计答案。
其实也很简单,我们求出了左右两边最近且比它大的值的位置的时候,直接把它的能量累加到这两个发射站的答案上去就可以了。
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
int n,k1[maxn],k2[maxn],a[maxn],b[maxn],sum[maxn],ans=-1;
stack<int> s;
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i];
}
for(int i=1;i<=n;i++){
while(s.size()&&a[s.top()]<a[i]){
k1[s.top()]=i;
s.pop();
}
s.push(i);
}
for(int i=n;i>=1;i--){
while(s.size()&&a[s.top()]<a[i]){
k2[s.top()]=i;
s.pop();
}
s.push(i);
}
for(int i=1;i<=n;i++){
sum[k1[i]]+=b[i];
sum[k2[i]]+=b[i];
}
for(int i=1;i<=n;i++){
ans=max(ans,sum[i]);
}
cout<<ans;
return 0;
}
例题3 乘积
不难发现每一个数作为最小值的时候,如果要想贡献最大,那就必须要找到它左右边最近的比它小的数(记为 \(l_i\) 和 \(r_i\)),因为包含这些数这个数就不是最小值了。同时要在这个基础上尽量延伸,所以第 \(i\) 个数作为最小值的贡献就是 \((\sum\limits_{j=l_i+1}\limits^{r_j-1} a_j) \times a_i\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+10;
int n,a[maxn],v[maxn],l[maxn],r[maxn],sum[maxn],ans;
stack<int> s1,s2;
int query(int l,int r){
return sum[r]-sum[l-1];
}
signed main(){
// freopen("big.in","r",stdin);
// freopen("big.out","w",stdout);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=sum[i-1]+a[i];
}
for(int i=1;i<=n;i++){
while(s1.size()&&a[s1.top()]>a[i]){
r[s1.top()]=i;
s1.pop();
}
s1.push(i);
}
for(int i=n;i>=1;i--){
while(s2.size()&&a[s2.top()]>a[i]){
l[s2.top()]=i;
s2.pop();
}
s2.push(i);
}
for(int i=1;i<=n;i++){
if(l[i]==0){
l[i]=1;
}
else{
l[i]++;
}
if(r[i]==0){
r[i]=n;
}
else{
r[i]--;
}
}
for(int i=1;i<=n;i++){
// cout<<l[i]<<" "<<r[i]<<endl;
ans=max(ans,query(l[i],r[i])*a[i]);
}
cout<<ans;
return 0;
}
单调队列
解决的问题
它可以在 \(O(n)\) 的时间内求出每个长度为 \(k\) 的区间中的最值。
但是存在感似乎很低:如果不卡,st 表和 线段树基本足矣。(哪个没木出题人会卡这种东西)
又不如更灵活的双指针。
所以就不写了。
st 表
解决的问题
st 表常用与解决可重复贡献问题。
可重复贡献问题就是对于单个数,将其多次算入答案中不会对答案产生影响。
例如区间 \(\mathsf{max\min}\)。
建立与查询
st 表建立在倍增的思想之上。这里我们拿区间最小值来举例。
我们令 \(\texttt{st}_{i,j}\) 为 \([i,i+2^j-1]\) 之间的最小值。
那么我们很显然就会有 \(\texttt{st}_{i,j}=\min(\texttt{st}_{i,j-1},\texttt{st}_{i+2^{j-1},j-1})\)。
这个操作其实就是在找最大的能够将这个区间全部覆盖的两个区间,将它们取 \(\min\) 即可。
查询同理,可以找到两个区间 \([l,l+2^{\lfloor \log(r-l+1) \rfloor}]\) 和 \([r-2^{\lfloor \log(r-l+1) \rfloor}+1,r]\) 来覆盖 \([l,r]\)。
code
#include<bits/stdc++.h>
using namespace std;
int n,m,a[100001],st[100001][31];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
st[i][0]=a[i];
}
for(int i=1;(1<<i)<=n;i++){
for(int j=1;j<=n;j++){
if(j+(1<<i)-1<=n){
st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);
}
}
}
for(int i=1;i<=m;i++){
int l,r,k;
scanf("%d%d",&l,&r);
k=log2(r-l+1);
printf("%d\n",max(st[l][k],st[r-(1<<k)+1][k]));
}
return 0;
}
例题 1 Iva & Pav
solution
首先我们注意到 \(\&\) 运算是有单调性的,所以考虑二分。
然后考虑快速维护 \(\&\) 运算。不难发现,区间按位与是一个可重复贡献问题(也就是说你将一个区间按位与起来的值再与上区间里的任何数答案都不变),所以可以使用 ST 表维护。
code
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
int n,m,x[maxn],st[maxn][20];
int query(int l,int r){
int k=log2(r-l+1);
return (st[l][k]&st[r-(1<<k)+1][k]);
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>x[i];
st[i][0]=x[i];
}
for(int i=1;(1<<i)<=n;i++){
for(int j=1;j<=n;j++){
if(j+(1<<i)-1<=n){
st[j][i]=(st[j][i-1]&st[j+(1<<(i-1))][i-1]);
}
}
}
cin>>m;
while(m--){
int l,k;
cin>>l>>k;
if(x[l]<k){
cout<<-1<<" ";
continue;
}
int L=l,R=n+1;
while(L<R){
int mid=L+R>>1;
if(query(l,mid)<k){
R=mid;
}
else{
L=mid+1;
}
}
cout<<L-1<<" ";
}
cout<<endl;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int t;
cin>>t;
while(t--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号