4.字符串合集2023-05-13

5.数论合集2023-05-12 6.学习笔记——树形dp2023-04-21 7.组合数学与线性代数合集2023-08-03 8.思想/套路合集2023-07-25 9.动态规划合集2023-08-09 10.搜索合集2023-09-10 11.图论合集2023-09-10

基本概念

有一个字符串 $s$ ，那么它的长度记作 $| s |$ 。

子串：由一个字符串 $s$ 的一段区间 $[l, r]$ 中的字符按顺序构成的字符串称为这个字符串的子串。

前缀：由一个字符串 $s$ 的一段区间 $[1, r]$ 中的字符按顺序构成的字符串称为这个字符串的前缀。特别地，当 $r < | s |$ 时，这个前缀称为真前缀。

后缀：由一个字符串 $s$ 的一段区间 $[l, | s |]$ 中的字符按顺序构成的字符串称为这个字符串的后缀。特别地，当 $l > 1$ 时，这个前缀称为真后缀。

border：对于一个字符串 $s$ ，既是 $s$ 的前缀又是 $s$ 的后缀的一个字符串称为 $s$ 的 border。

单模式串匹配

暴力匹配

在每个位置都进行一次匹配即可。

string a,b;
cin>>a>>b;
int sa=a.size(),sb=b.size();
for(int i=0;i<sa;i++){
	if(a[i]==b[0]){
		int f=1;
		for(int j=0;j<sb;j++){
			if(a[i+j]!=b[j])f=0;
		}
		if(f==1){
			cout<<i;
			return 0;
		}
	}
}

字符串哈希

字符串匹配为什么慢？

因为需要一位一位匹配。

如果我们将一个字符串转化为一个整数，那么匹配会快很多。

考虑如何将字符串转化为一个整数。

容易想到，直接将每个字符编号，然后加和就可以了。但是这种方法会把 ab 和 ba 一类字符串识别成同一个字符串，正确性不高。

我们需要一个正确性更高的算法。

我们记字符集大小为 $s$ 。

那么将一个字符串记为一个 $s$ 进制数，再转换为 $10$ 进制下的结果。

结果需要取模（令模数为 $p$ ）。

然后我们在字符串匹配的时候，通常需要获取一段区间的哈希值。

令 $h_{i}$ 为 $[1, i]$ 的哈希值。令 $n u m_{c}$ 为字符 $c$ 对应的编号，则 $h_{i} = h_{i - 1} \times s + n u m_{c}$ 。

那么 $[l, r]$ 的哈希值就是 $\frac{(h_{r} - h_{l - 1})}{s^{l - 1}}$ 。

实际运用中需要乘 $s^{l - 1}$ 在 $mod p$ 意义下的逆元。

例1 【模板】字符串哈希

直接哈希。甚至不用取区间。

这里底数我用 $131$ ，取模是 $unsigned long long$ 的自然溢出。

#include<bits/stdc++.h>
#define ull unsigned long long
using namespace std;
const int p=131;
int n,ans=1;
ull h[10001],Pow[10001];
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	Pow[0]=1;
	for(int i=1;i<=n;i++){
		string s;
		cin>>s;
		int len=s.size();
		ull hash=0;
		s=" "+s;
		for(int j=1;j<=len;j++){
			hash*=p;
			hash+=s[j];
		}
		h[i]=hash;
	}
	sort(h+1,h+n+1);
	for(int i=2;i<=n;i++){
		if(h[i]!=h[i-1]) ans++;
	}
	cout<<ans;
	return 0;
}

KMP

想想暴力匹配为什么会慢？

因为每次失配之后我们都要从头匹配。

KMP 就很好地优化了这一点，失配时，可以不需要再次重新匹配，而是可以找到当前位置失配时模式串应该从何处开始匹配。举个例子：

s: abcacababcab
t: abcab

令 $i$ 为文本串匹配到何处， $j$ 为模式串匹配到何处。

此时，我们在 $i = j = 5$ 时失配了。暴力的做法是 $i \to 2, j \to 1$ 然后继续匹配。而其实我们可以 $j \to 1$ 继续匹配：

s:abcacababcab
t:   abcab

为什么可以这么做？

因为我们扫完了模式串的前四位，发现字符串 a 是其 $4$ 位前缀 abca 的最长 border。那么就意味着我们在 $2, 3$ 位不可能匹配上，同时在 $4$ 位一定可以匹配其最长 border 的长度。

那么现在问题落在了怎么求解前缀的最长 border 上。（一般前 $i$ 位的最长 border 记为 $n e x t_{i}$ 或 $f a i l_{i}$ ）。

怎么计算 abacabab 的 $n e x t$ 数组？

考虑递推：

首先令 $n e x t_{1} = 0$ ， $i = 1, j = 2$ （ $i$ 是前缀最后一位， $j$ 是后缀最后一位）。

对于位置 $2$ ，由于 $s_{i} \neq s_{j}$ ，所以 $n e x t_{2} = 0$ ，然后 $j$ 加一。

对于位置 $3$ ，由于 $s_{i} = s_{j}$ ，所以 $n e x t_{3} = n e x t_{2} + 1 = 1$ ，然后 $i, j$ 加一。

对于位置 $4$ ，由于 $s_{i} \neq s_{j}$ ，所以 $n e x t_{4} = 0$ ，令 $i = 0$ ，然后 $j$ 加一。

同理可得 $n e x t_{5} = 1, n e x t_{6} = 2, n e x t_{7} = 3$ 。

对于位置 $8$ ，此时 $i = 4, j = 8$ ，我们发现 $s_{i} \neq s_{j}$ 。难道 $n e x t_{8} = 0$ 吗？

显然不是，既然现在这个前缀不能与 $s_{j}$ 组成一个公共前后缀，那么我们就考虑更短的，查表 $n e x t_{i} = 1$ ，即目前匹配上的 aba 的最长 border 为 a，于是这个 a 就有可能与 $s_{j}$ 组成一个 border，此时检查得 $n e x t_{8} = 2$ （要是还没匹配上就继续往后跳）。

因为匹配时候的 $i$ 是不会减的，所以 KMP 匹配的时间复杂度为 $O (| s | + | t |)$ 。

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
int nxt[maxn],lena,lenb,j; 
string a,b;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>a>>b;
	lena=a.size(),lenb=b.size();
	a=" "+a,b=" "+b; 
	for(int i=2;i<=lenb;i++){     
		while(j>0&&b[i]!=b[j+1]){
			j=nxt[j];  
		}  
		if(b[j+1]==b[i]){
			j++; 
		}   
		nxt[i]=j;
	}
	j=0;
	for(int i=1;i<=lena;i++){
		while(j>0&&b[j+1]!=a[i]){
			j=nxt[j];
		}
		if(b[j+1]==a[i]){
			j++;
		}
		if(j==lenb){
			cout<<i-lenb+1<<endl;
			j=nxt[j];
		}
	}
	for(int i=1;i<=lenb;i++){
		cout<<nxt[i]<<" ";
	}
	return 0;
}

STL 大法

清峥不让写

失配树

我们把一个字符串的一个位置的下标和它的 $n e x t$ 值之间连一条边（即对于 $1 \leq i \leq | s |$ ，对于 $i$ 和 $n e x t_{i}$ 连一条边）。

不难发现一个节点的所有祖先节点代表其所有的 border。

P3435 [POI2006] OKR-Periods of Words

题意

求给定字符串所有前缀的最大周期长度之和。

思路

我们有一个性质： $| s | - n e x t_{| s |}$ 是字符串 $s$ 的一个周期。（~~自证不难·~~）

对于一个字符串，我们不断跳 $n e x t$ 可以找到它的所有 border。

那么我们找到一个最小的 $n e x t$ （设为 $j$ ），答案加上 $i - j$ 就可以了。

暴力跳 next (65pts)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+10;
string s;
int nxt[maxn],n,ans;
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>s;
	s=" "+s;
	int x=0;
	for(int i=2;i<=n;i++){     
		while(x>0&&s[i]!=s[x+1]){
			x=nxt[x];  
		}  
		if(s[x+1]==s[i]){
			x++; 
		}   
		nxt[i]=x;
	}
	for(int i=1;i<=n;i++){
		int now=i;
		while(nxt[now]){
			now=nxt[now];
		}
		ans+=i-now;
	}
	cout<<ans;
	return 0;
}

优化1

如果我们找到 $i$ 对应最小的 $n e x t$ 为 $j$ ，那么就把 $n e x t_{i}$ 设为 $j$ ，下次跳可以一步到位。

记忆化 (100pts 3.82s)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+10;
string s;
int nxt[maxn],n,ans;
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>s;
	s=" "+s;
	int x=0;
	for(int i=2;i<=n;i++){     
		while(x>0&&s[i]!=s[x+1]){
			x=nxt[x];  
		}  
		if(s[x+1]==s[i]){
			x++; 
		}   
	   	nxt[i]=x;
	}
	for(int i=1;i<=n;i++){
		int now=i;
		while(nxt[now]){
			now=nxt[now];
		}
		ans+=i-now;
		if(nxt[i]) nxt[i]=now;
	}
	cout<<ans;
	return 0;
}

优化2

不难发现这是失配树上找离根节点最近的祖先的问题（求最短 border）。

那么我们干脆不要根节点 $0$ 了，然后像并查集一样路径压缩一下。

路径压缩 (100pts 250ms)

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+10;
string s;
int nxt[maxn],n,ans,f[maxn];
inline int find(int x){
	if(f[x]!=x) f[x]=find(f[x]);
	return f[x];
}
inline int search(int x){
	return x-f[x];
}
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>s;
	s=" "+s;
	int x=0;
	for(int i=1;i<=n;i++){
		f[i]=i;
	}
	for(int i=2;i<=n;i++){     
		while(x>0&&s[i]!=s[x+1]){
			x=nxt[x];  
		}  
		if(s[x+1]==s[i]){
			x++; 
		}   
		nxt[i]=x;
		if(nxt[i]){
			f[fa]=fb;
		}
	}
	for(int i=1;i<=n;i++){
		ans+=search(i);
	}
	cout<<ans;
	return 0;
}

字典树（Trie 树）

普通字典树

对于一堆字符串 $s_{1}, s_{2}, s_{3}, \dots, s_{n}$ ，如果我们想快速查找一个字符串 $t$ 在这一堆字符串中，有哪些是它的前缀，怎么做？

暴力扫显然是 $O (n \times | t |)$ 的。

假如我们的字符串是 i，int，integer，shw，shw666，intern 和 internet，那么我们可以建一颗树：

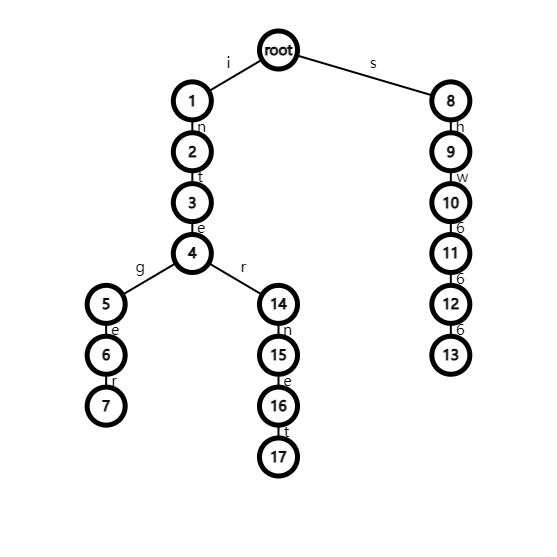
对于每个字符串，构建方法为：

首先， $n o w$ 指向根节点，然后遍历字符串：

若节点 $n o w$ 没有儿子 $s_{i}$ ，则创建一个节点 $s_{i}$ ， $c n t$ 加一并令 $n o w = c n t$ （ $c n t$ 为节点数量）；

否则直接跳到该儿子。

同时，我们记录一下哪些节点是一个字符串的结尾，那么对于每个询问，我们只要爬一遍树，看看路径上有哪些节点是被标记以该节点结尾的字符串，统计一下就是答案。

例如我们查找字符串 shw114514，此时爬树时会遇到 $10$ 号节点被标记，除此之外没有节点被标记，所以答案为 $1$ 。

题：P8306 【模板】字典树

#include<bits/stdc++.h> 
using namespace std;
const int maxn=3e6+10;
int t,n,q,trie[maxn][63],cnt,e[maxn];
int id(char c){
	if('a'<=c&&c<='z') return c-'a';
	else if('A'<=c&&c<='Z') return 26+c-'A';
	else return 52+c-'0';
}
void insert(string s){
	int len=s.size(),now=0;
	s=" "+s;
	for(int i=1;i<=len;i++){
		if(!trie[now][id(s[i])]){
			trie[now][id(s[i])]=++cnt;
		}
		now=trie[now][id(s[i])];
		e[now]++;
	}
}
int query(string s){
	int len=s.size(),now=0;
	s=" "+s;
	for(int i=1;i<=len;i++){
		if(trie[now][id(s[i])]){
			now=trie[now][id(s[i])];
		}
		else{
			return 0;
		}
	}
	return e[now];
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>t;
	while(t--){
		for(int i=0;i<=cnt;i++){
			for(int j=0;j<=114;j++){
				trie[i][j]=0; 
			}
		}
		for(int i=0;i<=cnt;i++){
			e[i]=0;
		}
		cnt=0;
		cin>>n>>q;
		for(int i=1;i<=n;i++){
			string s;
			cin>>s;
			insert(s);
		}
		for(int i=1;i<=q;i++){
			string s;
			cin>>s;
			cout<<query(s)<<endl;
		}
	}
	return 0;
}

01Trie

P4551 最长异或路径

给定一棵 $n$ 个点的带权树，结点下标从 $1$ 开始到 $n$ 。寻找树中找两个结点，求最长的异或路径。

$1 \leq n \leq 100000; 0 < u, v \leq n; 0 \leq w < 2^{31}$ 。

首先是一个很简单的处理：我们与处理出每个节点到根节点的异或值，记为 $s_{i}$ ，那么两个节点之间的异或路径就可以用 $s_{x} ⨁ x_{y}$ ，因为对于重复的路径，异或两次会消掉。

那么问题就变成了：计算 $max_{1 \leq i \leq n, 1 \leq j \leq n} s_{i} ⨁ s_{j}$ 。

我们对于每个 $s_{i}$ ，将它的二进制表示插入 Trie 中，然后对于每个 $s_{i}$ ，我们树上贪心，若第 $x$ 位为 $1$ ，那么如果这一个点有儿子 $0$ ，那么就往 $0$ 方向走，否则只能往 $1$ 方向走（因为异或是要求不同才是 $1$ ），反之亦然，然后取最大值就是答案了。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e6+10;
struct edge{
	int e,v;
};
int s[N],trie[N][2],n,cnt;
vector<edge> vec[N];
void dfs(int x,int fa){
	for(int i=0;i<vec[x].size();i++){
		int nx=vec[x][i].e;
		if(nx!=fa){
			s[nx]=s[x]^vec[x][i].v;
			dfs(nx,x);
		}
	}
}
void insert(int v){
	int now=0;
	for(int i=(1<<30);i;i>>=1){
		bool x=(v&i);
		if(!trie[now][x]){
			trie[now][x]=++cnt;
		}
		now=trie[now][x];
	}
}
int getval(int v){
	int ans=0,now=0;
	for(int i=(1<<30);i;i>>=1){
		bool x=(v&i);
		if(trie[now][!x]){
			ans+=i;
			now=trie[now][!x];
		}
		else{
			now=trie[now][x];
		}
	}
	return ans;
}
int main(){
	//freopen("data.txt","r",stdin);
	//freopen("my.txt","w",stdout); 
	std::ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	cin>>n;
	for(int i=1;i<n;i++){
		int u,v,w;
		cin>>u>>v>>w;
		vec[u].push_back((edge){v,w});
		vec[v].push_back((edge){u,w});
	}
	dfs(1,-1);
	for(int i=1;i<=n;i++){
		insert(s[i]);
	}
	int ans=0;
	for(int i=1;i<=n;i++){
		ans=max(ans,getval(s[i]));
	}
	cout<<ans;
	return 0;
}

多模式串匹配

下次一定

posted @ 2023-05-13 13:00 luqyou 阅读(85) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 数据结构合集

· 数据结构综合粗讲

· 字符串基础概念

· 字符串笔记

· 字符串入门

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话

公告

昵称： luqyou
园龄： 2年11个月
粉丝： 13
关注： 6

+加关注

2025年3月

日

一

二

三

四

五

六

luqyou

字符串合集