LeetCode (10): Regular Expression Matching [HARD]
https://leetcode.com/problems/regular-expression-matching/
【描述】
Implement regular expression matching with support for '.' and '*'.
'.' Matches any single character.
'*' Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
Some examples:
isMatch("aa","a") → false
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "a*") → true
isMatch("aa", ".*") → true
isMatch("ab", ".*") → true
isMatch("aab", "c*a*b") → true
【中文描述】
给两个字符串:s和p. p是正则表达式串,其中包含有三种字符:普通字符、'.'、'*'。要求实现方法,返回p是否能够匹配s.
其中:
'.'可以匹配s中任意字符。
'*'是个控制字符,在'*'前的字符在s中可以出现0或者无限次。
题目要求全部匹配,不能部分匹配。
例子:
isMatch("aa","a") → false //解释:s中2个a,而p中一个普通字符a,显然不匹配
isMatch("aa","aa") → true
isMatch("aaa","aa") → false
isMatch("aa", "a*") → true //解释:s中2个a,而p中有'a*',根据题意,a可以出现无数次,所以是匹配的
isMatch("aa", ".*") → true //解释:由于'.'可以代替任意字符,所以'.*'的意思就是任意字符出现任意次数,所以肯定可以匹配aa
isMatch("ab", ".*") → true //同上,ab也能匹配
isMatch("aab", "c*a*b") → true //解释:c在s中没有出现,但是c*是可以匹配的。然后aa匹配了a*, 最后的b互相匹配。 所以整体匹配
————————————————————————————————————————————————————————————
【初始思路】
刚开始没觉得是hard题,就觉得给2个指针,一个指s,一个指p。然后从前往后一步步比较就行了。无非就是比较当前位的时候兼顾后一位的情况,注意边界条件,仔细写应该不会出错。先写了一个,一提交wrong answer了。 用例是这样的:
s="aabbbcd", p="a*b*bbbcd"
显然,s和p是匹配的。但是用我上面的方法,就绝对匹配不成功。因为,p中的b*会直接和S中的bbb全部匹配,然后p中剩下的bbb就要和cd匹配,返回false。换句话说,我上面的算法是一条路走到黑,成功就成功,失败就失败。根本不考虑是否还有其他可能性!
【重整思路】
看到这个用例,我才反应过来,我太naive了,太没有程序猿的知觉了。事实上,仔细想想就能发现,这个题是需要回溯考虑的。可能按照s当前位和p中某'普通字符+*'模式比较是匹配的,到结尾有可能不匹配。但是如果当前位按照不与p中“字符+*”匹配(也即直接跳过p中'x*')走到最后却有可能成功。 所以,这就需要回溯考虑。如果按照既定步骤匹配到结尾不成功,我们可以回溯回来,然后从当前位用下一个策略去尝试一下。 所有的尝试里,只要成功一次,就算匹配成功!
说到回溯,程序猿的直觉告诉我,需要用递归Recursion!
【解法一:递归 Recursion】
回溯递归解法需要知道3个关键点:(1)如何确定当前步在哪里?(2)当前步有哪些决策?(3) 当前决策失败后回到哪里?
首先,如何确定当前步?由于已经考虑清楚要用递归,那么其实是不需要指针的。递归其实就是把大问题化为小问题的典型解题方案。本题的大问题是s和p是否匹配。假设s当前从左往右的一个子部分s1已经和p从左往右的一个子部分p1匹配了。那么剩下的子问题就是判断,s从s1后的部分和p从p1后的部分是否匹配的问题,这就把问题从大化小了。看下面图:
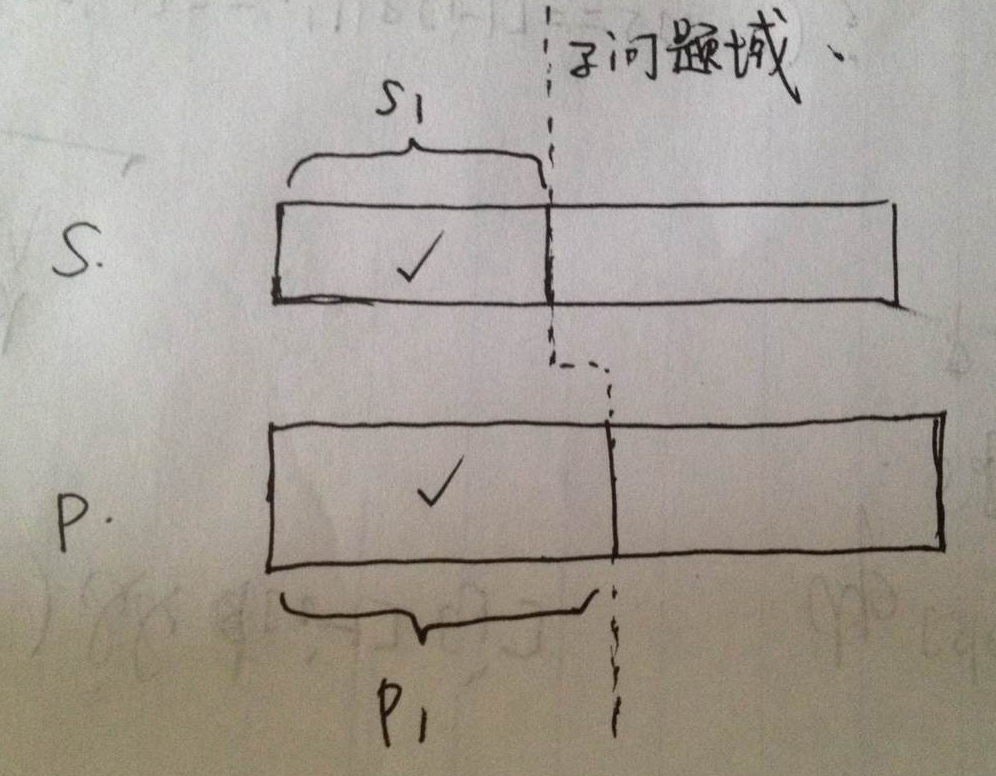
对于递归方法,由于传参要求都一样,所以显然,传进一个当前串的子串拷贝不就可以了么?
其次,当前有哪些决策,我们来分析一下,由于每次考虑的都是尚未进行匹配测试的子串,所以当前位置就是0位置:
(1) 当前p中下一个字符不为'*'的情况,这种情况下,p当前必须是'.'或者和s当前相同,才能匹配。如果匹配成功,那么s和p各自截取后一位子串继续递归。如果匹配不成功直接返回false。这是策略1;
(2) 当前p中下一个字符为'*'的情况,比较复杂,设当前字符为X。
(2.1) 首先初始假设,p当前的X*在s中根本没有出现过,所以,尝试一下把p后推2位,递归尝试一次。如果失败,说明s当前字符必须和p当前X匹配,然后才有可能成功。
(2.2) 2.1失败,只有X与s当前字符相同做匹配尝试有可能能成功。根据这个策略,s前移一位,p不动,递归尝试一次。如果返回失败,则可以认为必然失败。因为每个情况下,要么X*在s中匹配0次,也即策略1。 要么匹配1或无数次,这是策略2.2。 策略2.1已经失败,策略2.2也失败,没有其他策略可以选择了。所以肯定失败;
第三,怎么回溯?
首先,对于情况(1),s和p当前必须匹配,并且各推一位尝试成功,才能算成功,两个条件失败一个就肯定失败,所以不存在决策和回溯。
而对于情况(2),由于决策2.1和决策2.2成功一个即可,所以使用一个if-else判断。如果决策2.1成功,直接成功。 如果2.1失败,进入决策2.2 看看是否成功。
此外,递归方案必须考虑基准条件。什么是基准条件。s和p当前都是空串,肯定匹配,返回成功。p当前只有一个字符(因为上面每次都要考虑p下一个字符的问题,所以只有一个字符的时候是个特殊情况,需要单独拎出来考虑),这个时候,p当前字符必须和s当前字符匹配,并且s不能为空,才能算成功。
好了,到了这里,全部分析完了,可以编码。
【Show me the Code!!!】

1 /** 2 * 递归方法: 3 * 每次检查当前字符,有几种可能性: 4 * 1. p的下一个字符是*,那么首先考虑的可能性是S当前字符并不是p当前字符的通配出现, 也即初始假设p当前这个字符并没有在s中出现. 5 * 1.1 初始尝试,p指针后移2位递归求个结果,如果true,那肯定直接返回成功 6 * 1.2 初始尝试失败, 说明s当前字符需要和p当前字符匹配一下, 再递归一次, 看看结果. 如果还不行,那直接返回失败. 7 * 2. p的下一个字符不是*, 那么有2个可能性: p当前是. 或者 普通字符. 8 * 这两种情况下,都需要考虑和s当前字符的匹配情况,成功则指针后移,不成功则直接返回false 9 * @param s 待匹配串 10 * @param p 正则表达式 11 * @return 是否匹配的结果 12 */ 13 public static boolean isMatch(String s, String p) { 14 if(p.length() == 0) return s.length() == 0; 15 16 if(p.length() == 1) { 17 //这个返回的精妙之处在于,直接把对s的长度条件融入到了与条件里. 这个条件成立的时候,后面的条件才能拿来做最终的判断. 18 //如果s的长度条件不满足,那么后面不用判断了,肯定是false的. 19 //所以用了"&&",相当于以下2句的效果: 20 // if(s.length()==1) return p.charAt(0) == '.' || p.charAt(0) == s.charAt(0); 21 // else return false; 22 return s.length() == 1 && (p.charAt(0) == '.' || p.charAt(0) == s.charAt(0)); 23 } 24 25 //p.length()>1时, 看当前字符的下一个字符是什么了. 26 if(p.charAt(1) == '*') { 27 if(isMatch(s, p.substring(2))) return true;//初始假设 28 else { // 初始假设失败, s当前字符必须和p当前字符匹配,才有可能成功 29 // s.length() > 0 的意义上面讲过: 30 // 如果s已经为空串了,又已知p除去当前2个通配字符以后还有字符和s不匹配, 那就不用比了, 现在肯定也不匹配. 31 // 第二行的意义是, p当前还得是'.' 或者和s相同的字符 32 // 第三行的意义是, s跳过当前字符后,和p匹配了 33 // 以上三个条件都成立, 才能算最终可以匹配成功. 34 // 否则均失败 35 return s.length() > 0 36 && (p.charAt(0) == '.' || p.charAt(0) == s.charAt(0)) 37 && isMatch(s.substring(1), p); 38 } 39 } 40 41 //p当前字符下一个字符不是*, 最好处理 42 //匹配的条件是, 43 //1.s不为空串,因为s若为空串, 而p当前字符不是.就是普通字符,必须有个字符和它匹配,那必然失败 44 //2.p当前和s当前匹配 45 //3.p和s分别后移一位,也最终匹配 46 //1+2+3返回成功,才能算成功 47 else { 48 return s.length() > 0 49 && (p.charAt(0) == '.' || p.charAt(0) == s.charAt(0)) 50 && isMatch(s.substring(1), p.substring(1)); 51 } 52 }
【回溯法的反思】
递归的解法向来都是比较慢的,因为不是尾递归,每次递归栈中需要保存方法中全部变量信息,串长度一大,速度可想而知。还有没有更快的办法?更合理的办法?答案是肯定的。
【解法二:动态规划 DP】
动态规划的核心思想是,把算法执行过程中的中间结果保存起来,为了计算下一个状态,可以根据当前状态的结果递推得出。比如著名的菲波那切数列,1,1,2,3,5,8,13....,显然为了求当前的数字,只需要知道前面2个数字即可,之前的结果不再重要。但是如果用递归来解,那么之前的每一步的结果,都会保存在栈中,耗时耗空间。
此外,动态规划还适合解决只需要知道结果,而不关注中间过程的题目。如果,中间过程也需要给出,动态规划可能就不太适合了。
好了,既然是从前一个状态推当前状态,那么我们需要建立一个递推模型,然后找出递推公式(但凡用DP解题,这个是必须的!)。
【递推模型】
我们用一个二维数组来记录中间状态,并且数组元素就是boolean变量。比如dp[i][j]表示s中s{0,1,...i-1}子串和p中p{0,1,....j-1}子串的匹配情况。然后我们可以根据dp[i-1][j-1]的真假以及s{i-1}和p{j-1}的匹配情况,综合判断得出dp[i][j]的结果。
【递推公式】
既然我们用了2维数组,并且在递推的过程中要经常检查dp[i-1][j-1]这些情况,所以为防止越界,我们需要考虑先把数组的第一行和第一列先确定下来。
首先,显然的是,s为空串,p也为空串的情况下,dp[0][0]就表示了这个状态,显然 dp[0][0] = true。
同时,根据上面的递推模型来看,第一行dp[0][j]其实就表示了s为空串的时候,p和空串s匹配的情况。 而dp[i][0]表示,p为空串时,s各个字符和p匹配的情况。显然,dp[i][0]也就是第一列除第一行外肯定全部为false。因为p为空串,s只要不是空串就肯定不匹配。
我们来看看dp[0][j]的各个情况:
(1)j为1的时候,dp[0][1]=false。
(2)j>1的时候,p{j-1}=='*'为真并且dp[0][j-2]也为真,dp[0][j]才能为真。
这样,我们在正式递推之前,把这两个边界情况讨论清楚了。
由于前面已经把i==0和j==0情况下的边界讨论清楚了,所以我们的两个循环i和j都分别从1开始,到字符串最后一个字符停止。所以,用两个for循环可搞定。
为了求dp[i][j],其实要看p{j-1}的情况:
(1)p{j-1}!='*'情况:简单。p{j-1}必须和s{i-1}字符匹配。同时dp[i-1][j-1]必须匹配成功。这是个&&逻辑。
(2)p{j-1}=='*'情况,参考上面递归方法中的分析,假设p{j-2} = X, 所以目前有个*二元组:X*, 有2个不同的可能性:
(2.1) X在s中根本没有出现,那么dp[i][j] = dp[i][j-2] ;
(2.2) X在s中已经出现了1次或N次。1次的时候,p{j-2} == s{i-1}或者p{j-2}=='.',同时,dp[i-1][j]要为真,也即当前的p{0,...j-1}已经能匹配s{0,...i-2},那么前面条件如果成立,p{0....j-1}就也能匹配s{0,...i-1}。这两个条件是&&的关系,都得成立,才能算成功。
显然,2.1和2.2之间是||的关系。
到此,递推公式就出来了。然后按照递推公式去写就行了。最终,根据模型定义,dp[s.length][p.length]就是我们要求的结果: s{0,...slength-1} 与 p{0,...plength-1}的匹配情况。
【Show me the Code!!!】

1 /** 2 * 根据自己的理解写的DP, O(nm)时间, 但是空间是O(MN).时间应该是不能再优化了, 空间可优化成上面的O(slength) 3 * @param s 4 * @param p 5 * @return 6 */ 7 public static boolean isMatchDP(String s, String p) { 8 int slen = s.length(); 9 int plen = p.length(); 10 11 /** 12 * 保存动态规划的中间结果,我们用dp[i][j]来表示: S{0,..i-1} 与P{0,..j-1}的匹配结果. 13 */ 14 boolean dp[][] = new boolean[slen+1][plen+1];//上面解释了,i和j在dp里代表s和p的下标.所以,dp尺寸需要加1 15 16 /** 17 * 下面来分析一下递推公式(DP少不了这个东西!). 18 * 所谓递推公式就是根据之前已经保存的状态推出当前的状态. 也即求当前dp[i][j],可根据之前的结果间接的求出 19 * 假设当前求dp[i][j], 它代表了S{0->i-1}与P{0->j-1}的匹配情况. 那么有以下几个可能: 20 * (1)如果p{j-1}当前不是*,情况简单,当前匹配的唯一条件就是p{j-1}要与s{i-1}匹配 21 * 并且, 之前也都一直匹配, dp[i-1][j-1]匹配! 两者哪个不满足都是false,所以两个条件"&&"一下即可. 22 * 得递推公式: 23 * when p{j-1}!='*', dp[i][j] = dp[i-1][j-1] && p{j-1} == s{i-1} || p{j-1} == '.' 24 * (2)如果p{j-1}当前是个*, 情况比较复杂了. 首先看看有哪几种可能性, 我们设p{j-2} = X, X* 是个二元组 25 * (2.1) X没有在s中重复过, 也即X重复了0次, 所以这种情况就是只要dp[i][j-2]为true, 当前就可以为true. 26 * (2.2) X在S中...i-3,i-2,i-1的位置出现过>=1次, >=1可以拆分开理解,=1成立&&>1也成立!(这是本题最难的部分!一旦理解,这个题就是个easy题了!) 27 * 那么可以假设出现一次的话, 显然必须满足 p{j-2}==s{i-1}||p{j-2}=='.' 28 * 出现>1次, 还应要求, S{0->i-2}最起码要能匹配p{0->j-1}, 也即dp[i-1][j]也需为true 29 * 综上, 2.1和2.2之间是或者的关系,但是2.2内部,>=1我们拆成了>1&&=1的情况,这样就是个&&的关系 30 * 得递推公式: 31 * when p{j-1}=='*', dp[i][j] = dp[i][j-2] || (p{j-2}==s{i-1}||p{j-2}=='.') && dp[i-1][j] 32 * 有了递推公式, 我们可以看到,当i和j分别推进到各自边界的时候,两个串的最终匹配结果一定保存在dp[slen][plen],return这个结果就可以了! 33 */ 34 35 /** 36 * 显然 dp[0][0] = true, 因为代表两个空串做匹配的结果,肯定是true 37 */ 38 dp[0][0] = true; 39 40 /** 41 * 当p为空串的时候,s有字符,显然全部不可能匹配 42 */ 43 for(int i = 1; i <= s.length(); i++) { 44 dp[i][0] = false; 45 } 46 47 /** 48 * 显然, i=0, j从1-plen遍历的各个结果,代表了p各个子串分别是否能否匹配空串s. 49 * 有一定可能, 当p中j-1位置是*,并且0->j-3的匹配结果是true, 也即dp[0][j-2] = true 50 * 否则,dp[0][j] =false 51 * 这里, 我们把i=0的第一行计算出来 52 */ 53 for(int j = 1; j <= p.length(); j++) { 54 //之所以从1开始,是为了方便理解: j位置结果表示了p{0->j-1}的匹配结果 55 //所以,显然dp[0][1]代表了p第一个字符是否能够匹配空串, 显然是不可能的 56 if(j==1) dp[0][j] = false; 57 else dp[0][j] = p.charAt(j-1) == '*' && dp[0][j-2]; 58 } 59 60 61 62 /**到这里,我们就已经分析完了基本边界情况以及空串情况,下来开始递推*/ 63 for(int i = 1; i <= slen; i++) { 64 for(int j = 1; j <= plen; j++) { 65 if(p.charAt(j-1) != '*') { 66 dp[i][j] = dp[i-1][j-1] && (p.charAt(j-1) == '.' || p.charAt(j-1) == s.charAt(i-1)); 67 } 68 else { 69 dp[i][j] = dp[i][j-2]|| 70 (p.charAt(j-2) == '.' || p.charAt(j-2) == s.charAt(i-1)) && dp[i-1][j]; 71 } 72 } 73 } 74 return dp[slen][plen]; 75 }
【DP的反思】
上面这个DP时间复杂度是O(mn), 空间复杂度是O(mn)。 还是有优化余地的。在网上看大神的解法,有一个O(N)空间复杂度的解法很牛逼,这里贴出来,我还没有对单个字符为什么要从后往前匹配研究清楚,慢慢研究吧!

1 /** 2 * This is the O(nm) time and O(n) space DP, awesome! 3 * @param s 4 * @param p 5 * @return 6 */ 7 public static boolean isMatch(String s, String p) { 8 String[] patterns = new String[p.length()]; 9 int i = 0, ptr = 0; 10 while (i != p.length()) {//parse p into tokens[], 要么单字符,要么*二元组 11 if (i + 1 < p.length() && p.charAt(i + 1) == '*') { 12 patterns[ptr++] = p.substring(i, i + 2); 13 i += 2; 14 } 15 else { 16 patterns[ptr++] = p.substring(i, i + 1); 17 i += 1; 18 } 19 } 20 21 boolean[] d = new boolean[s.length() + 1]; 22 d[0] = true; 23 for (i = 1; i <= s.length(); ++i) d[i] = false; //d[]全部置为false 24 for (i = 1; i <= ptr; ++i) { 25 //根据tokens[], 一一判断是否和s中每个字符匹配. 26 String pattern = patterns[i - 1];//获取当前token 27 char c = pattern.charAt(0);//当前token第一个字符 28 if (pattern.length() == 2) {//2元组情况 29 for (int j = 1; j <= s.length(); ++j) {//分别针对s中字符进行匹配测试 30 d[j] = d[j] || (d[j - 1] && (c == '.' || c == s.charAt(j - 1))); 31 } 32 } 33 else {//单个情况 34 for (int j = s.length(); j >= 1; --j) { 35 d[j] = d[j - 1] && (c == '.' || c == s.charAt(j - 1)); 36 } 37 } 38 d[0] = d[0] && pattern.length() == 2; 39 } 40 return d[s.length()]; 41 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号