OpenGL ES学习笔记(二)
首先申明下,本文为笔者学习《OpenGL ES应用开发实践指南(Android卷)》的笔记,涉及的代码均出自原书,如有需要,请到原书指定源码地址下载。
《Android学习笔记——OpenGL ES的基本用法、绘制流程与着色器编译》中实现了OpenGL ES的Android版HelloWorld,并且阐明了OpenGL ES的绘制流程,以及编译着色器的流程及注意事项。本文将从现实世界中图形显示的角度,说明OpenGL ES如何使得图像在移动设备上显示的更加真实。首先,物体有各种颜色的变化,在OpenGL ES中为了生成比较真实的图像,对图像进行*滑着色是一种常见的操作。其次,移动设备存在横竖屏的切换,进行图像显示时,需要根据屏幕方向考虑屏幕的宽高比,使图像不因屏幕切换而变形。最后,现实中的物体都是三维的,我们观察物体都带有一定的视角,因此需要在OpenGL ES实现三维图像的显示。本文主要包括以下内容:
- *滑着色
- 自适应宽高
- 三维图像生成
一、*滑着色
*滑着色是通过在三角形的每个点上定义不同的颜色,在三角形的表面混合这些颜色得到的。那么,如何用三角形构成实际物体的表面呢?如何混合定义在顶点出的不同颜色呢?
首先引入三角形扇的概念。以一个中心顶点作为起始,使用相邻的两个顶点创建第一个三角形,接下来的每个顶点都会创建一个三角形,围绕起始的中心点按扇形展开。为了使扇形闭合,只需在最后重复第二个点。在OpenGL中通过GL_TRIANGLE_FAN指定数据代表三角形扇。
glDrawArrays(GL_TRIANGLE_FAN, 0, 6);
上述代码中,glDrawArrays的参数列表为:
// C function void glDrawArrays ( GLenum mode, GLint first, GLsizei count )
public static native void glDrawArrays(
int mode,
int first,
int count
);
可知,0代表第一顶点的位置,6表示6个顶点绘制一个三角形扇。
接下来会把每个点上的颜色定义为一个顶点属性,需要两部分的工作:(1)顶点数据;(2)着色器。《Android学习笔记——OpenGL ES的基本用法、绘制流程与着色器编译》中涉及到的顶点数据只有X/Y坐标,添加颜色属性,则在顶点坐标后增加了R/G/B值。具体格式如下:
float[] tableVerticesWithTriangles = {
// Order of coordinates: X, Y, R, G, B
// Triangle Fan
0f, 0f, 1f, 1f, 1f,
-0.5f, -0.5f, 0.7f, 0.7f, 0.7f,
0.5f, -0.5f, 0.7f, 0.7f, 0.7f,
0.5f, 0.5f, 0.7f, 0.7f, 0.7f,
-0.5f, 0.5f, 0.7f, 0.7f, 0.7f,
-0.5f, -0.5f, 0.7f, 0.7f, 0.7f,
};
同样的,相比于上一篇中涉及到的顶点着色器,增加颜色属性。
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
void main()
{
v_Color = a_Color;
gl_Position = a_Position;
gl_PointSize = 10.0;
}
这里需要说明的是varying变量,varying变量是*滑的关键。以直线AB为例,如果顶点A的a_Color是红色,顶点B的a_Color是绿色,那么,从A到B,将会是红色和绿色的混合。越接*顶点A,混合后的颜色显得越红;越接*顶点B,混合后的颜色就显示越绿。至于混合的算法,采用最基本的线性插值就可以完成。
在三角形表面混合时,与直线的线程插值相同,每个颜色在接*它的顶点处都是最强的,向其他顶点就会变暗,用比例确定每种颜色的相对权重,只是这里使用的是面积的比例,而不是线性插值所使用的长度。
回到AirHockeyRenderer中,首先在onSurfaceCreated体现颜色属性。
aPositionLocation = glGetAttribLocation(program, A_POSITION);
aColorLocation = glGetAttribLocation(program, A_COLOR);
// Bind our data, specified by the variable vertexData, to the vertex
// attribute at location A_POSITION_LOCATION.
vertexData.position(0);
glVertexAttribPointer(aPositionLocation, POSITION_COMPONENT_COUNT, GL_FLOAT,
false, STRIDE, vertexData);
glEnableVertexAttribArray(aPositionLocation);
// Bind our data, specified by the variable vertexData, to the vertex
// attribute at location A_COLOR_LOCATION.
vertexData.position(POSITION_COMPONENT_COUNT);
glVertexAttribPointer(aColorLocation, COLOR_COMPONENT_COUNT, GL_FLOAT,
false, STRIDE, vertexData);
glEnableVertexAttribArray(aColorLocation);
流程与《Android学习笔记——OpenGL ES的基本用法、绘制流程与着色器编译》中基本一致,只是添加了颜色属性。aColorLocation为颜色属性的位置,STRIDE为跨距,即tableVerticesWithTriangles数组中不仅包含顶点的坐标,还包含了颜色属性,因此在取顶点坐标时,需要跨越颜色属性。
vertexData.position(POSITION_COMPONENT_COUNT)指定OpenGL读取颜色属性时,需要从第一个颜色属性的位置开始,不是从第一个位置属性。
glVertexAttribPointer()关联颜色数据和着色器中的attribute vec4 a_Color。glVertexAttribPointer的参数列表如下,其通过调用native方法glVertexAttribPointerBounds实现。
// C function void glVertexAttribPointer ( GLuint indx, GLint size, GLenum type, GLboolean normalized, GLsizei stride, const GLvoid *ptr )
private static native void glVertexAttribPointerBounds(
int indx,
int size,
int type,
boolean normalized,
int stride,
java.nio.Buffer ptr,
int remaining
);
public static void glVertexAttribPointer(
int indx,
int size,
int type,
boolean normalized,
int stride,
java.nio.Buffer ptr
) {
glVertexAttribPointerBounds(
indx,
size,
type,
normalized,
stride,
ptr,
ptr.remaining()
);
}
在关联好颜色属性后,只需在AirHockeyRenderer的onDrawFrame绘制顶点数组即可,OpenGL会自动从顶点数据里读入颜色属性。
// Draw the table. glDrawArrays(GL_TRIANGLE_FAN, 0, 6); // Draw the center dividing line. glDrawArrays(GL_LINES, 6, 2); // Draw the first mallet. glDrawArrays(GL_POINTS, 8, 1); // Draw the second mallet. glDrawArrays(GL_POINTS, 9, 1);
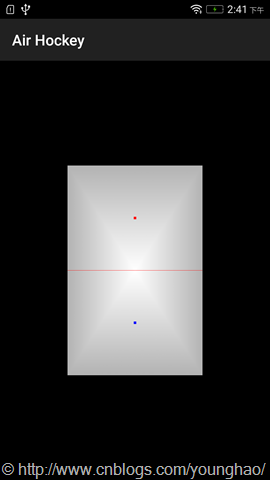
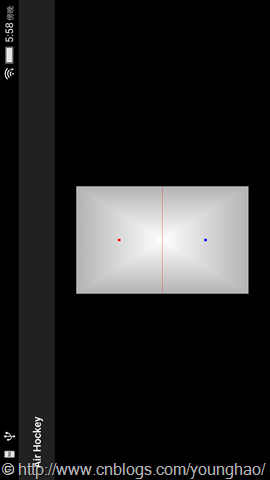
完成上述流程后,即可看到如下图所示的效果。
本节通过给顶点数据和顶点着色器增加颜色属性,并且使用跨距读入数据,最后通过varying在三角形*面上进行插值,使得两点之间的颜色得以*滑过渡。
二、自适应宽高
在Android开发中,横竖屏切换时需要加载不同的布局,采用OpenGL时,仍然存在屏幕大小、方向等的适配。OpenGL采用投影将真实世界映射到屏幕上,这种方式映射会使它在不同的屏幕尺寸或方向上看起来总是正确的。映射是通过矩阵变换来实现的,因此,这一节内容涉及到一些线性代数的基础内容。
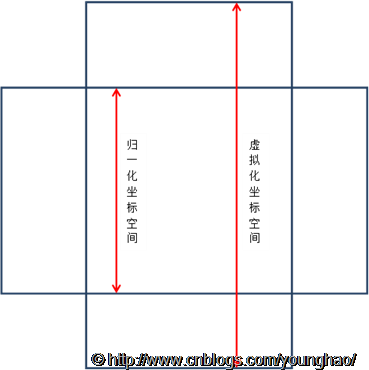
首先需要了解归一化坐标空间和虚拟坐标空间。之前使用的都是归一化坐标空间,即把一切物体都映射到x轴和y轴的[-1,1]空间内,独立于屏幕实际的尺寸和形状。因此,在实际Android设备上,以1280*720分辨率为例,归一化坐标空间中的正方形会被压扁。虚拟化坐标空间把较小的范围固定在[-1,1]内,而按照屏幕尺寸调整较大的范围。
把虚拟坐标空间转换会归一化坐标空间的核心就是正交投影。正交投影矩阵与*移矩阵类似,会把左右、上下、远*的事物映射到归一化设备坐标[-1,1]范围内。android.opengl包中的orthoM()方法可以生成一个正交投影矩阵,其参数列表为:
/**
* Computes an orthographic projection matrix.
*
* @param m returns the result
* @param mOffset
* @param left
* @param right
* @param bottom
* @param top
* @param near
* @param far
*/
public static void orthoM(float[] m, int mOffset,
float left, float right, float bottom, float top,
float near, float far) {
……
}
生成的正交投影矩阵的格式如下:
要理解正交投影矩阵如何转换虚拟坐标空间与归一化坐标空间,最好的办法是举个例子。
以1280*720分辨率的横屏模式为例,虚拟化坐标空间的x轴的范围是[-1280/720,1280/720],即[-1.78,1.78],屏幕本身为归一化坐标空间[-1,1],比如最右上角的点,在归一化坐标空间中的坐标为[1,1],而在虚拟化坐标空间中的坐标为[1.78,1]。经过上述正交投影矩阵转换之后,转换回归一矩阵。
将上述过程翻译为代码主要体现在三个地方:1)着色器;2)创建正交矩阵;3)传递矩阵给着色器。
uniform mat4 u_Matrix;
attribute vec4 a_Position;
attribute vec4 a_Color;
varying vec4 v_Color;
void main()
{
v_Color = a_Color;
gl_Position = u_Matrix * a_Position;
gl_PointSize = 10.0;
}
相比于之前的着色器,主要是设置gl_Position时,采用了u_Matrix与a_Position相乘,其中u_Matrix为上图中左边的正交投影矩阵,a_Position为右边的虚拟化坐标空间坐标,相乘得到gl_Position为归一化坐标空间坐标。
final float aspectRatio = width > height ?
(float) width / (float) height :
(float) height / (float) width;
if (width > height) {
// Landscape
orthoM(projectionMatrix, 0, -aspectRatio, aspectRatio, -1f, 1f, -1f, 1f);
} else {
// Portrait or square
orthoM(projectionMatrix, 0, -1f, 1f, -aspectRatio, aspectRatio, -1f, 1f);
}
orthoM通过传入不同的left-right,bottom-top参数生成针对横竖屏的正交投影矩阵。
// Assign the matrix glUniformMatrix4fv(uMatrixLocation, 1, false, projectionMatrix, 0);
// C function void glUniformMatrix4fv ( GLint location, GLsizei count, GLboolean transpose, const GLfloat *value )
public static native void glUniformMatrix4fv(
int location,
int count,
boolean transpose,
float[] value,
int offset
);
最后通过glUniformMatrix4fv方法将上述生成的正交投影矩阵传递给着色器。效果如下图所示,可以看出,在横竖屏模式下保持了同样的形状。
三、三维图像生成
在前一节中,为了使得物体能够自适应屏幕的宽高比变化,使用了正交投影(Orthographic Projection);为了实现三维效果显示,本节需要使用透视投影(Perspective Projection)。如果对投影矩阵的推导过程有兴趣的,可以参考《投影矩阵的推导(Deriving Projection Matrices)》,文中对正交投影以及透视投影的推导、使用做了详细的介绍。
OpenGL通过剪裁空间(Clip Space)的w分量做透视除法,得到三维效果。因此,从理论上讲,只要更新顶点坐标tableVerticesWithTriangles数组中的w分量(同时设置z分量)为合适的值,OpenGL就能自动实现三维显示。但实际操作中,一般不会硬编码w分量的值,而是通过透视投影矩阵来生成。通用的透视投影矩阵如下:
使用代码创建透视投影矩阵:
public static void perspectiveM(float[] m, float yFovInDegrees, float aspect, float n, float f) {
// 获取视野角度,即公式中的(阿尔法)
final float angleInRadians = (float) (yFovInDegrees * Math.PI / 180.0);
// 计算焦距,即公式中的a
final float a = (float) (1.0 / Math.tan(angleInRadians / 2.0));
// 生成矩阵
m[0] = a / aspect;
m[1] = 0f;
m[2] = 0f;
m[3] = 0f;
m[4] = 0f;
m[5] = a;
m[6] = 0f;
m[7] = 0f;
m[8] = 0f;
m[9] = 0f;
m[10] = -((f + n) / (f - n));
m[11] = -1f;
m[12] = 0f;
m[13] = 0f;
m[14] = -((2f * f * n) / (f - n));
m[15] = 0f;
}
在onSurfaceChanged中调用该方法创建透视矩阵,这里使用了45度的视野角度,并且距离*处*面距离为1,距离远处*面距离为10,由于采用右手坐标系,所以视椎体从z值为-1的位置开始,在z值为-10的位置结束。
MatrixHelper.perspectiveM(projectionMatrix, 45, (float) width/ (float) height, 1f, 10f);
因为没有指定z的位置,默认情况下它处于0的位置,因此,还需将物体进行*移。*移采用模型矩阵,模型矩阵可以通过OpenGL内置函数生成。
setIdentityM(modelMatrix, 0); translateM(modelMatrix, 0, 0f, 0f, -2.5f);
同时使用模型矩阵与透视矩阵需要注意矩阵乘法的顺序,直观的理解,将物体在空间沿任意轴*移不会改变物体在相对视点所观察到的形状,而透视则会改变。因此,应该先将物体做*移变换,后做透视。
公式中将投影矩阵放在左边,模型矩阵放在右边,正好实现了先将顶点进行*移,后进行透视的目的。
final float[] temp = new float[16]; multiplyMM(temp, 0, projectionMatrix, 0, modelMatrix, 0); System.arraycopy(temp, 0, projectionMatrix, 0, temp.length);
最后,还需要一步变化就可以看到真实的3D效果了,那就是旋转变化。旋转矩阵使用正弦和余弦三角函数把旋转角转换成缩放因子,同样,OpenGL提供了旋转矩阵的实现方法:
/**
* Rotates matrix m in place by angle a (in degrees)
* around the axis (x, y, z).
*
* @param m source matrix
* @param mOffset index into m where the matrix starts
* @param a angle to rotate in degrees
* @param x X axis component
* @param y Y axis component
* @param z Z axis component
*/
public static void rotateM(float[] m, int mOffset,
float a, float x, float y, float z) {
synchronized(sTemp) {
setRotateM(sTemp, 0, a, x, y, z);
multiplyMM(sTemp, 16, m, mOffset, sTemp, 0);
System.arraycopy(sTemp, 16, m, mOffset, 16);
}
}
将m矩阵旋转a度,可以分别针对x/y/z轴进行旋转。这里把物体绕x轴旋转-60度。
rotateM(modelMatrix, 0, -60f, 1f, 0f, 0f);
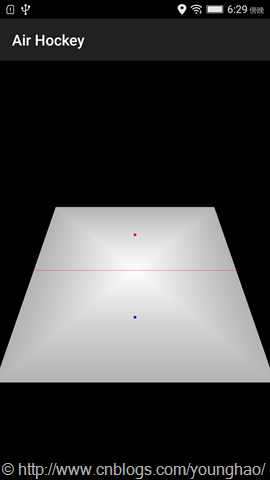
完成上述所有步骤之后,可以得到如下所示的效果图。
总结:
(1)通过插值实现顶点间颜色的*滑过渡;
(2)通过正交投影实现横竖屏切换时物体形状的保持;
(3)通过透视投影、*移变化、旋转变化实现物体的三维显示。



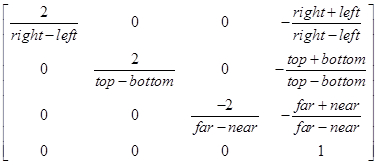
![clip_image002[6] clip_image002[6]](https://images2015.cnblogs.com/blog/826785/201601/826785-20160112174705319-1682606630.png)

![clip_image002[1] clip_image002[1]](https://images2015.cnblogs.com/blog/826785/201601/826785-20160113175200007-1521490292.png)
![clip_image002[7] clip_image002[7]](https://images2015.cnblogs.com/blog/826785/201601/826785-20160113175201928-812551853.png)