2021牛客寒假算法基础集训营1
A 串
题意
长度不超过nn,且包含子序列“us”的、只由小写字母构成的字符串有多少个? 答案对10^9+7取模。
所谓子序列,指一个字符串删除部分字符(也可以不删)得到的字符串。
例如,"unoacscc"包含子序列"us",但"scscucu"则不包含子序列"us"
样例 3 77
思路
比赛想排列组合没有想好,直接写挂了
看题解的方法,突然豁然开朗
分三种状态 : 没有u,有u后面没s,有us(f[i][0],f[i][1],f[i][2])
每一个i的状态转移(当前这个字符串往后加字符)
f[i][0]=f[i-1][0] * 25 (加一个除u的字符)
f[i][1]=f[i-1][1] * 25(加一个除s的字符)+ f[i-1][0](加u字符)
f[i][2]=f[i-1][2] * 26(随便加)+ f[i][i-1](加s字符)
#include <bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
const int N=1e6+10;
ll f[N][3];
int main(){
f[2][0]=25*25;f[2][1]=50;f[2][2]=1;
int n;scanf("%d",&n);
ll sum=1;
for(int i=3;i<=n;i++){
f[i][0]=f[i-1][0]*25%mod;
f[i][1]=(f[i-1][1]*25+f[i-1][0])%mod;
f[i][2]=(f[i-1][2]*26+f[i-1][1])%mod;
sum+=f[i][2];sum%=mod;
}
printf("%lld\n",sum);
return 0;
}
B 括号
题意
请你构造一个非空的括号字符串,包含正好 k 个不同合法括号对。
所谓括号字符串,是指由'('和')'这两种字符构成的字符串。
要求构造的字符串长度不超过100000。
思路
枚举一个例子 5 ())))) 7 ()))())
所以只要计算一下输入1e9字符串长度 我选了50000
#include <bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
const int N=1e6+10;
int a[N];
int main(){
int n;
scanf("%d",&n);
if(n<50000){
printf("(");
for(int i=0;i<n;i++){
printf(")");
}
printf("\n");
}
else{
int zhi=n/50000;int yu=50000-n%50000;
for(int i=0;i<zhi;i++){
printf("(");
}
for(int i=0;i<yu;i++){
printf(")");
}
if(yu!=50000){
printf("(");
}
for(int i=0;i<50000-yu;i++){
printf(")");
}
printf("\n");
}
return 0;
}
C 红和蓝
题意
你拿到了一棵树,请你给每个顶点染成红色或蓝色。
要求:每个红点周围有且仅有一个红点,每个蓝点周围有且仅有一个蓝点。
“周围”的定义:某点周围的点指通过邻边直接连接的点。
所谓树,即没有自环、重边和回路的无向连通图。
思路
构造树题目,首先能想到奇数个肯定是-1,那么偶数个的话基本是两两对应,那么直接从最底层,爸爸和儿子相对应,如果有重复则说明不行,然后在进行染色,第一个dfs两两分配(顺便找是否有矛盾的),第二个dfs染色即可
#include<bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(false)
#define mem(a,b) memset(a,b,sizeof(a))
#define pii pair<int,int>
#define ll long long
#define mod 1000000007
const double pi = acos(-1);
using namespace std;
const int N = 1e5+10;
int head[N],ne[N<<1],to[N<<1];
int n,q,tot=0,flag=0,cnt=0;
int color[N],vis[N];
void add(int u,int v){
to[tot]=v;
ne[tot]=head[u];
head[u]=tot++;
}
void dfs(int fa,int u){
int ge=0;//cout<<fa<<u<<endl;
for(int i=head[u];~i;i=ne[i]){
if(to[i]==fa)continue;
ge++;
dfs(u,to[i]);
}
if(!ge || !vis[u]){
if(vis[fa]){
flag=1;return;
}
vis[u]=vis[fa]=++cnt;
}
}
void dfs2(int fa,int u){
//cout<<fa<<u<<endl;
for(int i=head[u];~i;i=ne[i]){
if(to[i]==fa)continue;
if (vis[to[i]]==vis[u]) color[to[i]]=color[u];
else color[to[i]]=color[u]^1;
dfs2(u,to[i]);
}
}
int main(){
mem(head,-1);
IOS;
cin>>n;
for(int i=0;i<n-1;i++){
int u,v;cin>>u>>v;
add(u,v);add(v,u);
}
if(n&1){cout<<"-1";return 0;}
dfs(0,1);
if(flag){cout<<"-1";return 0;}
color[1]=1; dfs2(0,1);
for(int i=1;i<=n;i++){
if(color[i])cout<<"R";
else cout<<"B";
}
return 0;
}
/*
4
1 2
1 3
3 4
*/
E 三棱锥之刻
题意
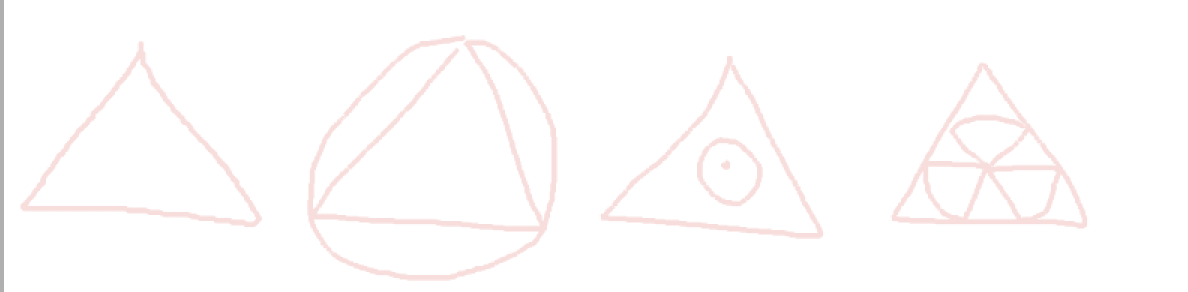
牛牛站在一个棱长为的正三棱锥内部的中心。(牛牛是不可移动的)(所谓正三棱锥,指六条棱都相等的三棱锥。正三棱锥的中心指到 4 个顶点距离都相等的那个点)\ • 如上图,牛牛站在P点,他拿着一个染色喷雾,可以用来给正三棱锥的内表面染色。已知喷雾能喷洒的距离为。也就是说,三棱锥内表面距离牛牛不超过的点才有可能被染色。牛牛想知道,正三棱锥内表面能被他染色的最大面积是多少?
ps:牛牛可看成一个无大小的点。重力对于喷雾的影响忽略不计。 1≤a,r≤1000
思路
一共四种情况 一种没碰到,一种全覆盖,一种覆盖成4个圆形,一种覆盖成4个(三个扇形面积加上三个三角形面积)
#include<bits/stdc++.h>
#define ll long long
const double pi = acos(-1.0);
using namespace std;
int main(){
double a,r,ans=0;
scanf("%lf%lf",&a,&r);
double mi = sqrt(6)*a/12;//内切球半径
double ma = sqrt(6)*a/4;//外接圆半径
double dd = sqrt(2)*a/4;
double d = sqrt(3)*a/6; //三角形内切圆半径
double r1 = sqrt(r*r-mi*mi);
if(r<mi) printf("0\n");//没覆盖
else if(r<=dd){//四个圆形
ans= pi*r1*r1*4;
printf("%.5f\n",ans);
}
else if(r<ma){//三个扇形面积加上三个三角形面积
double st1 = acos(d/r1)*2;// 三角形顶角角度
double st2 = (2*pi-st1*3)/3;//三个扇形的圆心角
double x = sqrt(r1*r1-d*d)*2; //三角形的底边
ans = (st2*r1*r1/2*3 + x/2*d*3)*4;
printf("%.5f\n",ans);
}
else{//全覆盖
printf("%.5f\n",sqrt(3)*a*a);
}
return 0;
}
I 限制不互素对的排列
题意
就是构造一个1~n数字里面有 k 个相邻gcd!=1的数组,k<=n/2
思路
n>=6之后 k==n/2 变成 3 6开头 ,其他用2的倍数即可,
n<6 可以枚举,其中有-1的情况
#include <bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
const int N=1e6+10;
int main(){
int n,k;
scanf("%d%d",&n,&k);
if(k==0){
for(int i=1;i<=n;i++)printf(i==n?"%d ":"%d\n",i);
}
else if(n>=6){
if(k==n/2){
printf("3 6");
for(int i=2;i<=n;i+=2){
if(i==6){continue;}
printf(" %d",i);
}
for(int i=1;i<=n;i+=2){
if(i==3){continue;}
printf(" %d",i);
}
printf("\n");
}
else{
int zhi=2*(k+1);
for(int i=2;i<=zhi;i+=2){
printf(i==2?"%d":" %d",i);
}
for(int i=1;i<=zhi;i+=2){
printf(" %d",i);
}
for(int i=zhi+1;i<=n;i++){
printf(" %d",i);
}
printf("\n");
}
}
else{
if(k==n/2){printf("-1\n");}
else{
printf("2 4");
for(int i=1;i<=n;i++){
if(i==2){continue;}
if(i==4){continue;}
printf(" %d",i);
}
printf("\n");
}
}
return 0;
}
J 一群小青蛙呱蹦呱蹦呱
题意
有n个格子,每个格子里有一个数,1,2,3,4...n牛牛放出无穷只青蛙。
第一只青蛙的路线是:1->2->4->8->16->....
第二只青蛙的路线是:1->3->9->27->81->....
第三只青蛙的路线是:1->5->25->125....
第四只青蛙的路线是:1->7->49........
用数学语言描述,第i只青蛙的路线是首项为1,公比为p(i)的等比数列,其中p(i)代表第个素数。
当青蛙跳到一个格子上,如果这个格子上面有一个数,青蛙就会把这个数吃掉。牛牛想知道,
所有没有被吃掉的数的lcm(最小公倍数 ,Least common multiple)是多少?由于这个lcm可能非常大,请输出它对10^9+7取模的值。N<=1.6 * 10^8
思路
因为2 去掉2 4 8 16 ……(2^k),那么3去掉3 9 27 ……(3^k)
lcm的话因子有两个及以上的因子的最高幂,那么除了2的另一个因子是3以外,其他都是2因子
p1^k1 * p2^k2 和 p1^k3 * p2^k4 的lcm==p1^max(k1,k3) * p2^max(k2,k4)
所以只要找出1.6 * 10^8里面的素数,这里用了 位图欧拉筛优化 (其实这里因为要找两个因子及以上的数字所以可以优化找0.8 * 10^8里面的素数)
#include<bits/stdc++.h>
using namespace std;
const int N =160000007;
int vis[N/32+50];
typedef long long ll ;
ll mod=1000000007;
ll pri[9000000],len=0;
ll sum[9000000];
bool Get(int i){
int x=i/32,y=i%32;
return 1<<y & vis[x];
}
void Set(int i){
int x=i/32,y=i%32;
vis[x]|=1<<y;
}
void init(){
len=0;
for(int i=2;i<=N;i++){
if(!Get(i))
pri[len++]=i;
for(int j=0;j<len&&i*pri[j]<=N;j++){
Set(i*pri[j]);
if(i%pri[j]==0) break;
}
}
sum[0]=pri[0];
for(int i = 1;i < len; i++) sum[i] = (ll)sum[i-1]*pri[i]%mod;
}
ll ksm(ll a,ll b){
ll ans=1;
while(b){
if(b&1){
ans*=a;ans%=mod;
}
a*=a;a%=mod;
b>>=1;
}
return ans;
}
ll solve(ll n)
{
ll ans=1;
for(int i=0;i<len;i++){
ll zhi=(i==0?3:2);
if(zhi*pri[i]>n) break;
ll t=1;
while(zhi*t*pri[i]<=n) t*=pri[i];
ans=ans*t%mod;
}
return ans;
}
int main(){
init();
ll n;
while(~scanf("%lld",&n)){
ll zhi=solve(n);
if(zhi==1){
printf("empty\n");
}
else printf("%lld\n",zhi);
}
return 0;
}


