Codeforces Round #620 (Div. 2) E

LCA的倍增

模板：

 

int fath[maxn][20], depth[maxn];
int dist[maxn],head[maxn];
void add(int u,int v,int dist0){
    a[tot].next=head[u];
    a[tot].dist=dist0;
    a[tot].v=v;
    head[u]=tot++;
}
void dfs(int u,int fa,int d) {
    fath[u][0]=fa; depth[u]=d;
    for(int i=1;i<20;i++) fath[u][i]=fath[fath[u][i-1]][i-1];
    for (int i=head[u];~i;i=a[i].next){
        int v=a[i].v;if(v==fa)continue;
        dist[v]=dist[u]+a[i].dist;
        dfs(v,u,d+1);
    }
}
void init(int n){
    for(int i=0;i<=n;i++)fath[i][0]=0,dist[i]=0,head[i]=-1,depth[i]=0;
    tot=0;
}
inline int lca(int x,int y){
    if(depth[x]<depth[y])swap(x,y);
    int h=depth[x]-depth[y];
    for(it i=0;h>0;i++){
        if(h&1){
            x=fath[x][i];
        }
        h>>=1;
    }
    if(x==y)return x;
    for(it i=19;i>=0;i--){
        if(fath[x][i]!=fath[y][i]){
            x=fath[x][i];
            y=fath[y][i];
        }
    }
    return fath[x][0];
}
inline int dis(int u,int v){
    int d=lca(u,v);
    return dist[u]+dist[v]-2*dist[d];
}

 

 

 

 

题意：

给一个n点的数，以1为根的树，

询问m个x,y,a,b,k

问x，y两点暂时联通，a点到b点能不能刚好满足过k条线

能输出yes，不能输出no

思路：

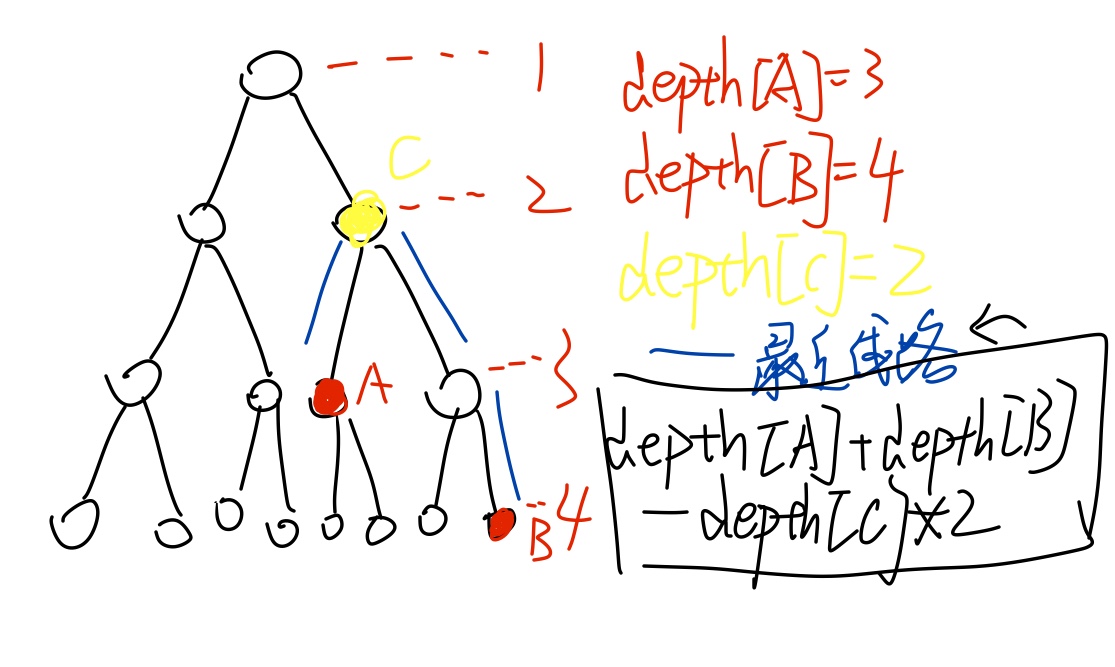
树上两点之间的距离用lca算出来，因为可以反复横跳，所以只要两点之间的距离小于等于k，然后与k的奇偶性一样就是yes

一共有三条路

dis（a，b）

dis（a，x）+dis（y，b）+1

dis（a，y）+dis（x，b）+1

 

 

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define il inline
#define it register int
#define inf 0x3f3f3f3f
#define lowbit(x) (x)&(-x)
#define mem(a,b) memset(a,b,sizeof(a))
#define mod 998244353
const int maxn=1e5+10;
struct node{
    int next,v;
}a[maxn<<1];
int t,m,n,head[maxn],tot,x,y,a1,b,k,f,depth[maxn],fa[maxn][20];
void add(int u,int v){
    a[tot].next=head[u];
    a[tot].v=v;head[u]=tot++;
}
void build(int uu){
    queue<int>q;
    depth[uu]=1;
    q.push(1);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(it i=head[u];~i;i=a[i].next){
            int v=a[i].v;
            if(depth[v]==-1){
                depth[v]=depth[u]+1;q.push(v);
                fa[v][0]=u;
                for(it j=1;j<=19;j++){
                    int arc=fa[v][j-1];
                    fa[v][j]=fa[arc][j-1];
                }
            }
        }
    }
}
int lca(int x,int y){
    if(depth[x]<depth[y])swap(x,y);
    for(it i=19;i>=0;i--){
        if(depth[fa[x][i]]>=depth[y]){
            x=fa[x][i];
        }
    }
    if(x==y)return x;
    for(it i=19;i>=0;i--){
        if(fa[x][i]!=fa[y][i]){
            x=fa[x][i];
            y=fa[y][i];
        }
    }
    return fa[x][0];
}
int dis(int u,int v){
    int d=lca(u,v);
    return depth[u]+depth[v]-2*depth[d];
}
int main(){
    mem(head,-1);mem(depth,-1);tot=0;
    scanf("%d",&n);
    for(it i=0;i<n-1;i++){
        int u,v;
        scanf("%d%d",&u,&v);add(u,v);add(v,u);
    }
    depth[0]=0;build(1);
    scanf("%d",&m);
    while(m--){
        scanf("%d%d%d%d%d",&x,&y,&a1,&b,&k);
        int kk=k;k%=2;
        int d1=dis(a1,b),d2=dis(a1,x)+dis(y,b)+1,d3=dis(a1,y)+dis(x,b)+1;
        if((d1%2==k && kk>=d1) || (d2%2==k && kk>=d2)||(d3%2==k && kk>=d3)){printf("YES\n");}
        else{printf("NO\n");}
    }
    return 0;
}
/*
5
1 2
2 3
3 4
4 5
5
1 3 1 2 2
1 4 1 3 2
1 4 1 3 3
4 2 3 3 9
5 2 3 3 9
YES
YES
NO
YES
NO
*/