【数据结构1-3】集合—并查集

一.并查集实现原理

 

为了解释并查集的原理，我将举一个更有爱的例子。

话说江湖上散落着各式各样的大侠，有上千个之多。他们没有什么正当职业，整天背着剑在外面走来走去，碰到和自己不是一路人的，就免不了要打一架。但大侠们有一个优点就是讲义气，绝对不打自己的朋友。而且他们信奉“朋友的朋友就是我的朋友”，只要是能通过朋友关系串联起来的，不管拐了多少个弯，都认为是自己人。这样一来，江湖上就形成了一个一个的群落，通过两两之间的朋友关系串联起来。而不在同一个群落的人，无论如何都无法通过朋友关系连起来，于是就可以放心往死了打。但是两个原本互不相识的人，如何判断是否属于一个朋友圈呢？

 

我们可以在每个朋友圈内推举出一个比较有名望的人，作为该圈子的代表人物，这样，每个圈子就可以这样命名“齐达内朋友之队”“罗纳尔多朋友之队”……两人只要互相对一下自己的队长是不是同一个人，就可以确定敌友关系了。

 

但是还有问题啊，大侠们只知道自己直接的朋友是谁，很多人压根就不认识队长，要判断自己的队长是谁，只能漫无目的的通过朋友的朋友关系问下去：“你是不是队长？你是不是队长？”这样一来，队长面子上挂不住了，而且效率太低，还有可能陷入无限循环中。于是队长下令，重新组队。队内所有人实行分等级制度，形成树状结构，我队长就是根节点，下面分别是二级队员、三级队员。每个人只要记住自己的上级是谁就行了。遇到判断敌友的时候，只要一层层向上问，直到最高层，就可以在短时间内确定队长是谁了。由于我们关心的只是两个人之间是否连通，至于他们是如何连通的，以及每个圈子内部的结构是怎样的，甚至队长是谁，并不重要。所以我们可以放任队长随意重新组队，只要不搞错敌友关系就好了。于是，门派产生了。

 

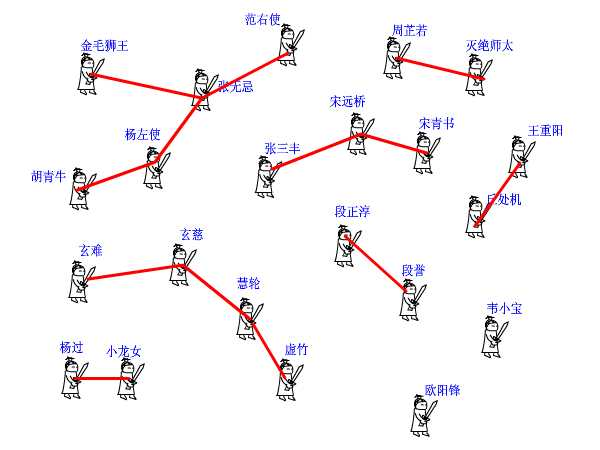
下面我们来看并查集的实现。 int father[1000]; 这个数组，记录了每个大侠的上级是谁。大侠们从1或者0开始编号（依据题意而定），father[15]=3就表示15号大侠的上级是3号大侠。如果一个人的上级就是他自己，那说明他就是掌门人了，查找到此为止。也有孤家寡人自成一派的，比如欧阳锋，那么他的上级就是他自己。每个人都只认自己的上级。比如胡青牛同学只知道自己的上级是杨左使。张无忌是谁？不认识！要想知道自己的掌门是谁，只能一级级查上去。 find这个函数就是找掌门用的，意义再清楚不过了（路径压缩算法先不论，后面再说）。

int find(int x)
{
    return far[x]==x?x:find(far[x]);//简化版 没有路径压缩
}

 

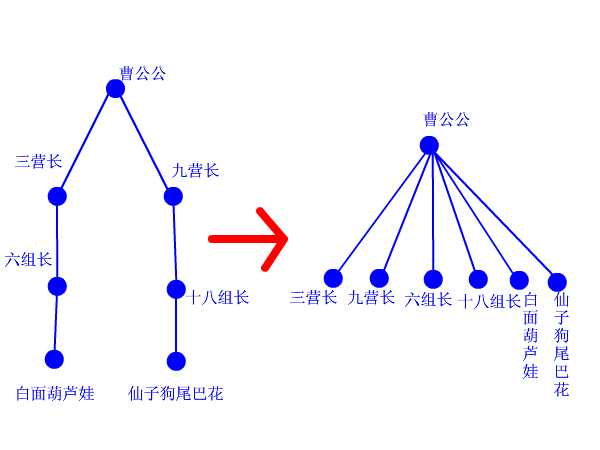
再来看看路径压缩算法。建立门派的过程是用merge函数两个人两个人地连接起来的，谁当谁的手下完全随机。最后的树状结构会变成什么胎唇样，我也完全无法预计，一字长蛇阵也有可能。这样查找的效率就会比较低下。最理想的情况就是所有人的直接上级都是掌门，一共就两级结构，只要找一次就找到掌门了。哪怕不能完全做到，也最好尽量接近。这样就产生了路径压缩算法。 设想这样一个场景：两个互不相识的大侠碰面了，想知道能不能揍。 于是赶紧打电话问自己的上级：“你是不是掌门？” 上级说：“我不是呀，我的上级是谁谁谁，你问问他看看。” 一路问下去，原来两人的最终boss都是东厂曹公公。 “哎呀呀，原来是记己人，西礼西礼，在下三营六组白面葫芦娃!” “幸会幸会，在下九营十八组仙子狗尾巴花！” 两人高高兴兴地手拉手喝酒去了。 “等等等等，两位同学请留步，还有事情没完成呢！”我叫住他俩。 “哦，对了，还要做路径压缩。”两人醒悟。 白面葫芦娃打电话给他的上级六组长：“组长啊，我查过了，其习偶们的掌门是曹公公。不如偶们一起及接拜在曹公公手下吧，省得级别太低，以后查找掌门麻环。” “唔，有道理。” 白面葫芦娃接着打电话给刚才拜访过的三营长……仙子狗尾巴花也做了同样的事情。 这样，查询中所有涉及到的人物都聚集在曹公公的直接领导下。每次查询都做了优化处理，所以整个门派树的层数都会维持在比较低的水平上。路径压缩的代码，看得懂很好，看不懂也没关系，直接抄上用就行了。总之它所实现的功能就是这么个意思。

int find(int x)
{
    return far[x]==x?x:far[x]=find(far[x]);//路径压缩版
}

 

例：P1551 亲戚

 AC代码：

#include<iostream>
using namespace std;
int far[5001];
int find(int x)
{
    return far[x]==x?x:far[x]=find(far[x]);
}//查找爸爸，如果爸爸是自己，意思是没有爸爸 返回即可
int combine(int tmp1, int tmp2)
{
    return far[find(tmp2)] = find(tmp1);
}//将两颗子树合并在一起，比如这里的意思就是把tmp2的祖宗挂在tmp1的祖宗下面
int main()
{
    int tmp1, tmp2;
    int n, m, p;
    cin >> n >> m >> p;
    for (int i = 1; i <= n; i++)
        far[i] = i;//初始化
    for (int i = 0; i < m; i++)
    {
        cin >> tmp1 >> tmp2;
        combine(tmp1, tmp2);
    }//并查集
    for (int i = 0; i < p; i++)
    {
        cin >> tmp1 >> tmp2;
        printf(find(tmp1) == find(tmp2) ?"Yes" : "No");//想一想为什么不可以直接far[tmp1]==far[tmp2];
        cout << endl;
    }
}