【算法1-1】模拟与高精度—减法篇

本文大部分思路，代码来源于 stone_juice石汁

本人加以改动符合自己的思维过程；

一.搞定高精度数的存储

当long long都解决不了数的存储时，用数组存储，且为了后续计算方便，读取高精度数时用string类型读取。

 

for (int i = 1; i <= s1.length(); i++)
        arr1[i] = s1[s1.size() - i] - '0';
    for (int i = 1; i <= s2.length(); i++)
        arr2[i] = s2[s2.size() - i] - '0';

 

 

 

二.如何计算

当arr1里面的每一位数都大于arr2里面的每一位数时

 

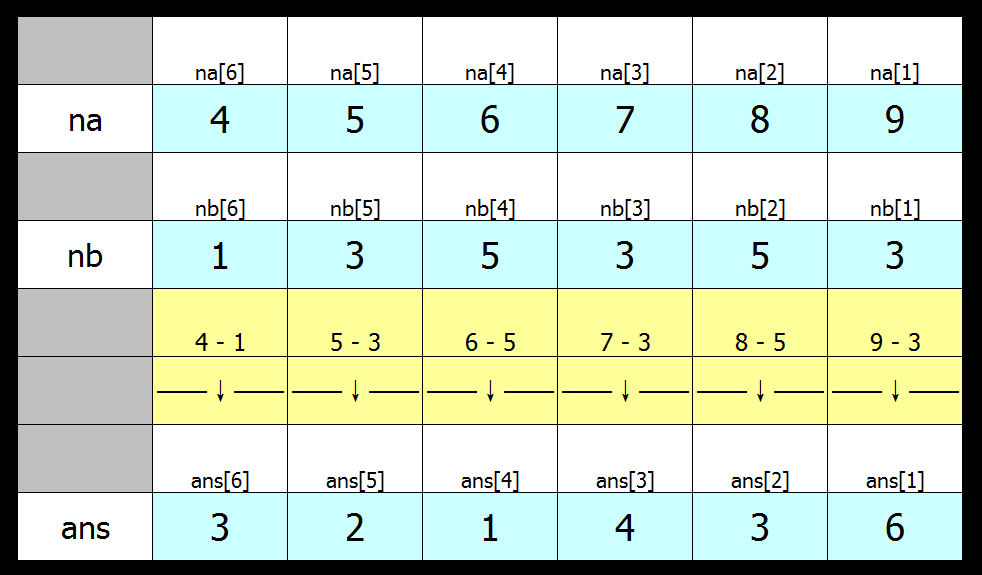
当arr1里面的每一位数有小于arr2里面的位数时，即当前数加10，前面一个数减1

 

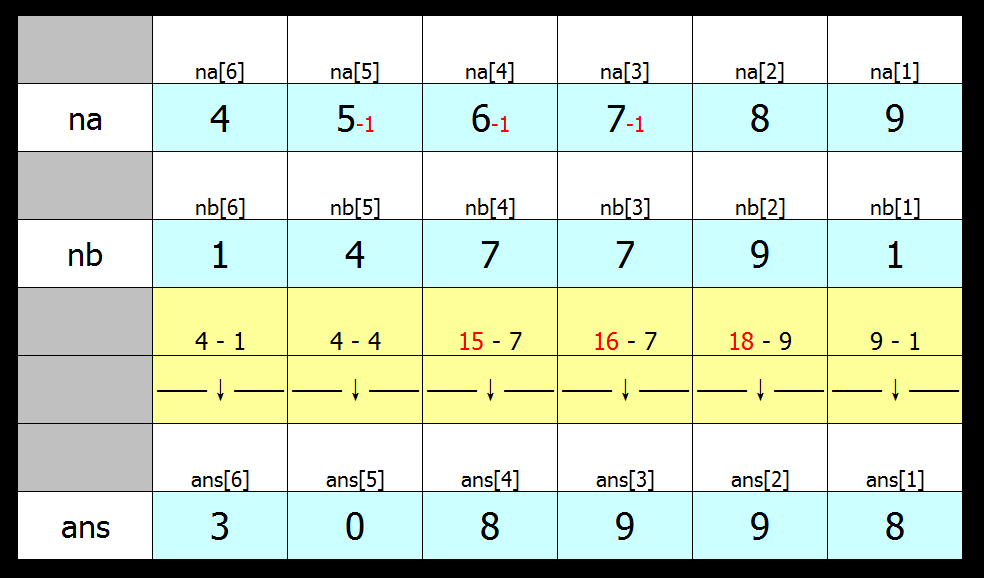
for (int i = 1; i <= maxl; i++)
    {
        if (arr1[i] < arr2[i])
        {
            arr1[i + 1]--;
            arr1[i] += 10;
        }
        ans[i] = arr1[i] - arr2[i];
    }

 

三.一些小bug

首先需要解决的几个坑点：

①前导零如何去除

比如 100001-100000=00001；

 

    while (ans[maxl] == 0)
        maxl--;

 

②本身结果为零如何输出

比如 100000-100000=0；

 

if (maxl < 1)
        return "0";

 

③小数减大数怎么办

比如 999-1000=-1；

 

if (s1.length() < s2.length() || (s1.length() == s2.length() && s1 < s2))
    {
        return "-" + jianfa(s2, s1);
    }

 

四.多次计算怎么办

直接写成函数，在main函数里面调用即可；

终极代码（注意，此代码不能解决a,b两个数＜0的情况）

 

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int arr1[200000], arr2[200000], ans[200000];
string jianfa(string s1, string s2)
{
    int maxl = max(s1.length(), s2.length());
    string ss;
    if (s1.length() < s2.length() || (s1.length() == s2.length() && s1 < s2))
    {
        return "-" + jianfa(s2, s1);
    }
    for (int i = 1; i <= s1.length(); i++)
        arr1[i] = s1[s1.size() - i] - '0';
    for (int i = 1; i <= s2.length(); i++)
        arr2[i] = s2[s2.size() - i] - '0';
    for (int i = 1; i <= maxl; i++)
    {
        if (arr1[i] < arr2[i])
        {
            arr1[i + 1]--;
            arr1[i] += 10;
        }
        ans[i] = arr1[i] - arr2[i];
    }
    while (ans[maxl] == 0)
        maxl--;
    if (maxl < 1)
        return "0";
        for (int i = maxl; i >0; i--)
            ss += ans[i] + '0';
    return ss;
}
int main()
{
    string s1, s2;
    cin >> s1 >> s2;
    cout << jianfa(s1, s2);
}