树状数组&线段树复习笔记
树状数组
基本结构
示意图:
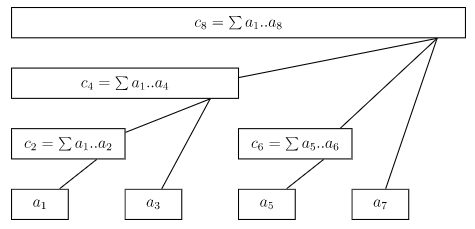
1~8各数码之间的关系
| 原数 | 无符号原码 | 有符号补码 | 负数的补码 | lowbit(x&(-x)) |
|---|---|---|---|---|
| 1 | 0001 | 00001 | 11111 | 0001 |
| 2 | 0010 | 00010 | 11110 | 0010 |
| 3 | 0011 | 00011 | 11101 | 0001 |
| 4 | 0100 | 00100 | 11100 | 0100 |
| 5 | 0101 | 00101 | 11011 | 0001 |
| 6 | 0110 | 00110 | 11010 | 0010 |
| 7 | 0111 | 00111 | 11001 | 0001 |
| 8 | 1000 | 01000 | 11000 | 1000 |
线段树中各层级之间的关系
| \({i}\) | 所属的树形层级 | 层级间的二进制关系 |
|---|---|---|
| 1 | 1, 2, 4, 8 | 0001>0010>0100>1000 |
| 2 | 2, 4, 8 | 0010>0100>1000 |
| 3 | 3, 4, 8 | 0011>0100>1000 |
| 4 | 4, 8 | 0100>1000 |
| 5 | 5, 6, 8 | 0101>0110>1000 |
| 6 | 6, 8 | 0110>1000 |
| 7 | 7, 8 | 0111>1000 |
| 8 | 8 | 1000 |
显然我们可以发现点 \(i\) 所属树形结构之间的关系,因此可以得到第一个操作,单点修改
单点修改&区间求和
单点修改:
void add(int x, int y){
for (; x <= n; x += x & -x) c[x] += y;
}
从小层级逐层向上修改
区间查询:
int ask(int x){
int res = 0;
for (; x; x -= x & -x)
res += c[x];
return res;
}
void work(){
int l = read(), r = read();
//if (l > r) swap(l, r);
printf("%d\n", ask(r)-ask(l-1));
}
很显然,ask函数就是吧 add 的操作反过来,进行前缀和的计算,最后 ask(r)-ask(l-1) 就是区间和
区间修改&区间查询
考场上显然我会用线段树来完成这个操作
区间修改首先考虑差分
考虑维护序列 \(a\) 的差分数组 \(b\),此时可知 \(a_i = \sum\limits_{j=1}^{i}b_j\),要求 \(\sum\limits_{i=1}^{r}a_i\) 的值
\(\begin{aligned} & \sum\limits_{i=1}^{r}a_i \\ = & \sum\limits_{i=1}^{r}\sum\limits_{j=1}^{i}b_j \\ = & \sum\limits_{i=1}^{r}b_i \times (r - i + 1) \\ = & \sum\limits_{i=1}^{r}b_i \times (r + 1) - \sum\limits_{i=1}^{r}b_i \times i \end{aligned}\)
因此,我们发现 \(a\) 的前缀和可以由 \(b\) 的两个前缀和相减得到
所以我们只需要建两颗树状数组分别维护 \(\sum b_i\) 和 \(\sum b_i \times i\) 即可
Code:
const int MAXN = 600010;
int a[MAXN], n, m;
long long c[2][MAXN], sum[MAXN];
long long ask(int k, int x){
long long ans = 0;
for (; x; x -= x & -x) ans += c[k][x];
return ans;
}
void add(int k, int x, int y){
for (; x <= n; x += x & -x) c[k][x] += y;
}
void work(){
n = read(), m = read();
for (int i = 1; i <= n; i++)
a[i] = read(), sum[i] = sum[i-1] + a[i];
while (m--){
int falg = read();
if (falg == 1){
int x = read(), y = read(), k = read();
add(0, x, k);
add(0, y+1, -k);
add(1, x, x * k);
add(1, y+1, -(y+1) * k);
}
else{
int x = read(), y = read();
long long ans = sum[y] + (y+1) * ask(0, y) - ask(1, y);
ans -= sum[x-1] + x * ask(0, x-1) - ask(1, x-1);
printf("%lld\n", ans);
}
}
}
注:
1 l r k把区间 \([l, r]\) 中的每一项增加 \(k\)2 l r求区间 \([l, r]\) 中的每一个数的和
例题瞎扯
题目大意
给定一个长度为 \(n (n \le 10^5)\) 的数列 \(a (a_i \le 10^{12})\),有 \(m (m \le 10^5)\) 次操作,有两种操作:
0 l r把区间 \([l, r]\) 中每一个数开平方(向下取整)1 l r求区间 \([l, r]\) 中数的和
基本思路
首先维护区间很容易想到线段树与树状数组,但显然此题用线段树是杀鸡用牛刀
机房有大佬用分块的,还有奆佬用珂朵莉树,离谱
接下来可以发现一个显然的性质,\(\forall a_i\) 最多开方 \(6\) 次就会变成 \(1\)
我们可以借鉴一下并查集的思想,新建一个 \(fa\) 数组来维护
当 \(a_i \ne 1\) 时,\(fa_i = i\),否则 \(fa_i = i + 1\)
至于修改就直接暴力即可
Code
点击查看代码
const int MAXN = 100033;
long long t[MAXN*4], a[MAXN];
int n, m, fa[MAXN];
int find(int x){
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
inline void add(int x, long long y){
for(; x <= n; x += (x&-x))
t[x] += y;
}
inline long long ask(int x){
long long res = 0;
for (; x; x -= (x&-x))
res += t[x];
return res;
}
int main(){
n = read();
for (int i = 1; i <= n; i++)
a[i] = read(), fa[i] = i, add(i, a[i]);
m = read();
while (m--){
int q = read(), l = read(), r = read(), t;
if (l > r)
swap(l, r);
if (q == 1)
printf("%lld\n", ask(r) - ask(l-1));
else
for (int i = l; i <= r; i = (find(i) == i) ? i + 1 : fa[i])
add(i, (t = (int)sqrt(a[i])) - a[i]), a[i] = t, fa[i] = (a[i] <= 1) ? i + 1: i;
}
return 0;
}
线段树
结构
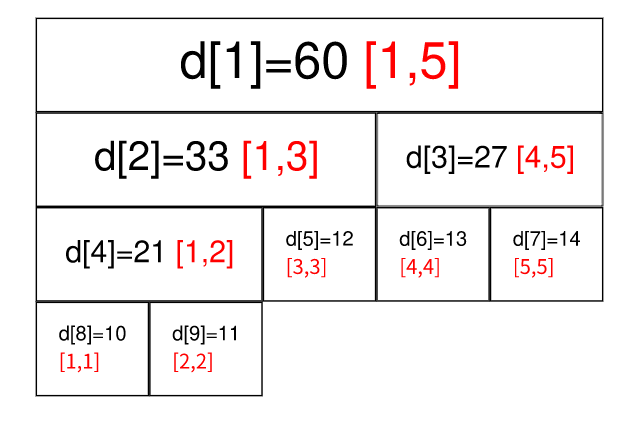
线段树的结构还是比较好理解的,就是不断二分,直到区间长度为 \(1\)
好理解归好理解,但代码量比树状数组不知道高出了多少
写这篇文章的时候,线段树我还记得,但树状数组不记得了
建树
递归建树即可(以求区间和为例)
const int MAXN = 100010;
int a[MAXN], n, m;
struct SegmentTree{
int l, r;
long long sum;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
}t[MAXN*4];
void build(int p, int l, int r){
l(p) = l, r(p) = r;
if (l == r){
sum(p) = a[l];
return;
}
int mid = (l + r) >> 1;
//int mid = l + ((r - l) >> 1);(l+r>2147483647)
build(p*2, l, mid);
build(p*2+1, mid+1, r);
sum(p) = sum(p*2) + sum(p*2+1);
}
区间查询
和树状数组思路差不多,只不过这里是利用递归计算
long long ask(int p, int l, int r){ //当前为p节点,总区间为[l,r],l(p)与r(p)表示当前区间
if (l <= l(p) && r >= r(p)) return sum(p); //如果完全覆盖
//spread(p);
int mid = (l(p)+r(p)) >> 1; //向下递归
long long res = 0;
if (l <= mid) res += ask(p*2, l, r);
if (r > mid) res += ask(p*2+1, l ,r);
return res;
}
区间修改(加)
为什么没有单点修改?树状数组不像吗?
此处如果要把每一层的节点都扫描一遍去更新答案,时间复杂度将会爆炸
因此此处要引入一个懒标记(延迟标记)。
就是当此段区间被完全覆盖时,就给它加上懒标记
当此段区间被询问或部分修改时,将懒标记下传并更新。
区间加+区间查询:
const int MAXN = 100010;
int a[MAXN], n, m;
struct SegmentTree{
int l, r;
long long sum, add;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define add(x) t[x].add
}t[MAXN*4];
void build(int p, int l, int r){
l(p) = l, r(p) = r;
if (l == r){
sum(p) = a[l];
return;
}
int mid = (l + r) >> 1;
build(p*2, l, mid);
build(p*2+1, mid+1, r);
sum(p) = sum(p*2) + sum(p*2+1);
}
void spread(int p){ //懒标记的下传
if (add(p)){
sum(p*2) += add(p) * (r(p*2) - l(p*2) + 1);
sum(p*2+1) += add(p) * (r(p*2+1) - l(p*2+1) + 1);
add(p*2) += add(p);
add(p*2+1) += add(p);
add(p) = 0;
}
}
void change(int p, int l, int r, int d){
if(l <= l(p) && r >= r(p)){
sum(p) += (long long)d * (r(p) - l(p) + 1);
add(p) += d; //打上懒标记
return;
}
spread(p); //若要拆分此区间,先下传懒标记
int mid = (l(p) + r(p)) >> 2;
if (l <= mid) change(p*2, l, r, d);
if (r > mid) change(p*2+1, l, r, d);
sum(p) = sum(p*2) + sum(p*2+1);
}
long long ask(int p, int l, int r){
if (l <= l(p) && r >= r(p)) return sum(p);
spread(p);
int mid = (l(p)+r(p)) >> 1;
long long ans = 0;
if (l <= mid) ans += ask(p*2, l, r);
if (r > mid) ans += ask(p*2+1, l ,r);
return ans;
}
void work(){
n = read(), m = read();
for (int i = 1; i <= n; i++)
a[i] = read();
build(1, 1, n);
while (m--){
int flag = read();
if (flag == 1){
int l = read(), r = read(), k = read();
//if (l > r) swap(l, r);
change(1, l, r, k);
}
else{
int l = read(), r = read();
//if (l > r) swap(l, r);
printf("%lld\n", ask(1, x, y));
}
}
}
区间加+区间乘+区间查询
加法与乘法的懒标记要分开存,注意下放时先更新乘法懒标记,后更新加法懒标记
Code
const int MAXN = 100010;
int a[MAXN], n, m, mo;
struct SegmentTree{
int l, r;
long long sum, add = 0, mul = 1;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define add(x) t[x].add
#define mul(x) t[x].mul
}t[MAXN*4];
void build(int p, int l, int r){
l(p) = l, r(p) = r;
if (l == r){
sum(p) = a[l];
return;
}
int mid = (l + r) >> 1;
build(p*2, l, mid);
build(p*2+1, mid+1, r);
sum(p) = sum(p*2) + sum(p*2+1);
}
void spread(int p){
//更新每段的和
sum(p*2) = (sum(p*2) * mul(p) + add(p) * (r(p*2) - l(p*2) + 1)) % mo;
sum(p*2+1) = (sum(p*2+1) * mul(p) + add(p) * (r(p*2+1) - l(p*2+1) + 1)) % mo;
//先更新乘法懒标记,后更新加法懒标记
mul(p*2) = (mul(p*2) * mul(p)) % mo;
mul(p*2+1) = (mul(p*2+1) * mul(p)) % mo;
add(p*2) = (add(p*2) * mul(p) + add(p)) % mo;
add(p*2+1) = (add(p*2+1) * mul(p) + add(p)) % mo;
//懒标记归位
mul(p) = 1;
add(p) = 0;
}
void change_add(int p, int l, int r, int d){
if(l <= l(p) && r >= r(p)){
sum(p) += d * (r(p) - l(p) + 1), sum(p) %= mo;
add(p) += d, add(p) %= mo;
return;
}
spread(p);
int mid = (l(p) + r(p)) / 2;
if (l <= mid) change_add(p*2, l, r, d);
if (r > mid) change_add(p*2+1, l, r, d);
sum(p) = sum(p*2) + sum(p*2+1), sum(p) %= mo;
}
void change_mul(int p, int l, int r, int d){
if(l <= l(p) && r >= r(p)){
sum(p) *= d, sum(p) %= mo;
mul(p) *= d, mul(p) %= mo;
add(p) *= d, add(p) %= mo;
return;
}
spread(p);
int mid = (l(p) + r(p)) / 2;
if (l <= mid) change_mul(p*2, l, r, d);
if (r > mid) change_mul(p*2+1, l, r, d);
sum(p) = sum(p*2) + sum(p*2+1), sum(p) %= mo;
}
long long ask(int p, int l, int r){
if (l <= l(p) && r >= r(p)) return sum(p) % mo;
spread(p);
int mid = (l(p)+r(p)) >> 1;
long long ans = 0;
if (l <= mid) ans += ask(p*2, l, r), ans %= mo;
if (r > mid) ans += ask(p*2+1, l ,r), ans %= mo;
return ans % mo;
}
void work(){
n = read(), m = read(), mo = read();
for (int i = 1; i <= n; i++)
a[i] = read() % mo;
build(1, 1, n);
while (m--){
int flag = read();
if (flag == 1){
int x = read(), y = read(), k = read() % mo;
change_mul(1, x, y, k);
}
else if (flag == 2){
int x = read(), y = read(), k = read() % mo;
change_add(1, x, y, k);
}
else{
int x = read(), y = read();
printf("%lld\n", ask(1, x, y) % mo);
}
}
}
区间最大子段和(单点修改)
整体思路和刚刚差不多,只是维护上有些区别
为了维护区间最大子段和,需要维护当前区间的最大子段和,最大前缀和,最大后缀和
合并时取两段区间的各自的最大子段和与前一个区间的最大后缀和加后一个区间的最大前缀和中的最大值
Code
const int MAXN = 500010, inf = 0x7fffffff;
int a[MAXN], n, m;
struct SegmentTree{
int l, r, sum;
int lmax, rmax, mmax;
#define l(x) t[x].l
#define r(x) t[x].r
#define sum(x) t[x].sum
#define m(x) t[x].mmax
#define lm(x) t[x].lmax
#define rm(x) t[x].rmax
}t[MAXN*4];
void update(int p){
sum(p) = sum(p<<1) + sum(p<<1|1);
lm(p) = max(sum(p<<1)+lm(p<<1|1), lm(p<<1));
rm(p) = max(sum(p<<1|1)+rm(p<<1), rm(p<<1|1));
m(p) = max(max(m(p<<1), m(p<<1|1)), rm(p<<1)+lm(p<<1|1));
}
void build(int p, int l, int r){
l(p) = l, r(p) = r;
if (l == r){
sum(p) = m(p) = lm(p) = rm(p) = a[l];
return;
}
int mid = (l + r) >> 1;
build(p<<1, l, mid);
build(p<<1|1, mid+1, r);
update(p);
}
void change(int p, int x, int d){
if(l(p)== r(p)){
sum(p) = m(p) = lm(p) = rm(p) = d;
return;
}
int mid = (l(p) + r(p)) >> 1;
if (x <= mid) change(p<<1, x, d);
if (x > mid) change(p<<1|1, x, d);
update(p);
}
SegmentTree ask(int p, int l, int r){
if (l <= l(p) && r(p) <= r) return t[p];
int mid = (l(p) + r(p)) >> 1;
if(r <= mid) return ask(p<<1, l, r);
if(l > mid) return ask(p<<1|1, l, r);
SegmentTree x = ask(p<<1, l, r), y = ask(p<<1|1, l, r), re;
re.sum = x.sum + y.sum;
re.lmax = max(x.sum+y.lmax, x.lmax);
re.rmax = max(y.sum+x.rmax, y.rmax);
re.mmax = max(max(x.mmax, y.mmax), x.rmax+y.lmax);
return re;
}
void work(){
n = read(), m = read();
for (int i = 1; i <= n; i++)
a[i] = read();
build(1, 1, n);
while (m--){
int flag = read();
if (flag == 1){
int x = read(), y = read();
if (x > y) swap(x, y);
printf("%d\n", ask(1, x, y).mmax);
}
else{
int x = read(), y = read();
change(1, x, y);
}
}
}

 数据结构真毒瘤
数据结构真毒瘤
