算法竞赛专题解析(5):简单数据结构
本系列是这本算法教材的扩展资料:《算法竞赛入门到进阶》(京东 当当 ) 清华大学出版社
如有建议,请联系:(1)QQ 群,567554289;(2)作者QQ,15512356
本文写给刚学过编程语言,正在学数据结构的新队员。
在《数据结构》教材中,一般包含这些内容:线性表(数组、链表)、栈和队列、串、多维数组和广义表、哈希、树和二叉树、图(图的存储、遍历等)、排序等。
本文给出几个简单数据结构的详细代码和习题:链表、栈和队列。
其他几种数据结构的代码和习题,例如串、二叉树、图,在《算法竞赛入门到进阶》一书中有详细说明,这里不再重复。
1 链表
链表的特点是:用一组任意的存储单元存储线性表的数据元素(这组存储单元可以是连续的,也可以不连续)。链表是容易理解和操作的基本数据结构,它的操作有:初始化、添加、遍历、插入、删除、查找、排序、释放等。
下面用例题洛谷 P1996,给出动态链表、静态链表、STL链表等5种实现方案。其中有单向链表,也有双向链表。在竞赛中,为加快编码速度,一般用静态链表或者STL list。
本文给出的5种代码,经过作者的详细整理,逻辑和流程完全一样,看懂一个,其他的完全类似,可以把注意力放在不同的实现方案上,便于学习。
洛谷P1996 https://www.luogu.com.cn/problem/P1996
约瑟夫问题
题目描述:n个人围成一圈,从第一个人开始报数,数到 m 的人出列,再由下一个人重新从 1 开始报数,数到 m 的人再出圈,依次类推,直到所有的人都出圈,请输出依次出圈人的编号。
输入输出:输入两个整数 n,m。输出一行n个整数,按顺序输出每个出圈人的编号。1≤m,n≤100。
输入输出样例:
输入
10 3
输出
3 6 9 2 7 1 8 5 10 4
1.1 动态链表
教科书都会讲动态链表,它需要临时分配链表节点、使用完毕后释放链表节点。这样做,优点是能及时释放空间,不使用多余内存。缺点是很容易出错。
下面代码实现了动态单向链表。
#include <bits/stdc++.h>
struct node{ //链表结构
int data;
node *next;
};
int main(){
int n,m;
scanf("%d %d",&n,&m);
node *head,*p,*now,*prev; //定义变量
head = new node; head->data = 1; head->next=NULL; //分配第一个节点,数据置为1
now = head; //当前指针是头
for(int i=2;i<=n;i++){
p = new node; p->data = i; p->next = NULL; //p是新节点
now->next = p; //把申请的新节点连到前面的链表上
now = p; //尾指针后移一个
}
now->next = head; //尾指针指向头:循环链表建立完成
//以上是建立链表,下面是本题的逻辑和流程。后面4种代码,逻辑流程完全一致。
now = head, prev=head; //从第1个开始数
while((n--) >1 ){
for(int i=1;i<m;i++){ //数到m,停下
prev = now; //记录上一个位置,用于下面跳过第m个节点
now = now->next;
}
printf("%d ", now->data); //输出第m节点,带空格
prev->next = now->next; //跳过这个节点
delete now; //释放节点
now = prev->next; //新的一轮
}
printf("%d", now->data); //打印最后一个,后面不带空格
delete now; //释放最后一个节点
return 0;
}
1.2 用结构体实现单向静态链表
上面的动态链表,需要分配和释放空间,虽然对空间的使用很节省,但是容易出错。在竞赛中,对内存管理要求不严格,为加快编码速度,一般就静态分配,省去了动态分配和释放的麻烦。这种静态链表,使用预先分配的大数组来存储链表。
静态链表有两种做法,一是定义一个链表结构,和动态链表的结构差不多;一种是使用一维数组,直接在数组上进行链表操作。
本文给出3个例子:用结构体实现单向静态链表、用结构体实现双向静态链表、用一维数组实现单向静态链表。
下面是用结构体实现的单向静态链表。
#include <bits/stdc++.h>
const int maxn = 105; //定义静态链表的空间大小
struct node{ //单向链表
int id;
//int data; //如有必要,定义一个有意义的数据
int nextid;
}nodes[maxn];
int main(){
int n, m;
scanf("%d%d", &n, &m);
nodes[0].nextid = 1;
for(int i = 1; i <= n; i++){
nodes[i].id = i;
nodes[i].nextid = i + 1;
}
nodes[n].nextid = 1; //循环链表:尾指向头
int now = 1, prev = 1; //从第1个开始
while((n--) >1){
for(int i = 1; i < m; i++){ //数到m,停下
prev = now;
now = nodes[now].nextid;
}
printf("%d ", nodes[now].id); //带空格
nodes[prev].nextid = nodes[now].nextid; //跳过节点now,即删除now
now = nodes[prev].nextid; //新的now
}
printf("%d", nodes[now].nextid); //打印最后一个,后面不带空格
return 0;
}
1.3 用结构体实现双向静态链表
#include <bits/stdc++.h>
const int maxn = 105;
struct node{ //双向链表
int id; //节点编号
//int data; //如有必要,定义一个有意义的数据
int preid; //前一个节点
int nextid; //后一个节点
}nodes[maxn];
int main(){
int n, m;
scanf("%d%d", &n, &m);
nodes[0].nextid = 1;
for(int i = 1; i <= n; i++){ //建立链表
nodes[i].id = i;
nodes[i].preid = i-1; //前节点
nodes[i].nextid = i+1; //后节点
}
nodes[n].nextid = 1; //循环链表:尾指向头
nodes[1].preid = n; //循环链表:头指向尾
int now = 1; //从第1个开始
while((n--) >1){
for(int i = 1; i < m; i++) //数到m,停下
now = nodes[now].nextid;
printf("%d ", nodes[now].id); //打印,后面带空格
int prev = nodes[now].preid;
int next = nodes[now].nextid;
nodes[prev].nextid = nodes[now].nextid; //删除now
nodes[next].preid = nodes[now].preid;
now = next; //新的开始
}
printf("%d", nodes[now].nextid); //打印最后一个,后面不带空格
return 0;
}
1.4 用一维数组实现单向静态链表
这是最简单的实现方法。定义一个一维数组\(nodes[]\),\(nodes[i]\)的\(i\)是节点的值,\(nodes[i]\)的值是下一个节点。
从上面描述可以看出,它的使用环境也很有限,因为它的节点只能存一个数据,就是\(i\)。
#include<bits/stdc++.h>
int nodes[150];
int main(){
int n, m;
scanf("%d%d", &n, &m);
for(int i=1;i<=n-1;i++) //nodes[i]的值就是下一个节点
nodes[i]=i+1;
nodes[n]=1; //循环链表:尾指向头
int now = 1, prev = 1; //从第1个开始
while((n--) >1){
for(int i = 1; i < m; i++){ //数到m,停下
prev = now;
now = nodes[now]; //下一个
}
printf("%d ", now); //带空格
nodes[prev] = nodes[now]; //跳过节点now,即删除now
now = nodes[prev]; //新的now
}
printf("%d", now); //打印最后一个,不带空格
return 0;
}
1.5 STL list
竞赛或工程中,常常使用C++ STL list。list 是双向链表,它的内存空间可以是不连续的,通过指针来进行数据的访问,它能高效率地在任意地方删除和插入,插入和删除操作是常数时间的。
请读者自己熟悉list的初始化、添加、遍历、插入、删除、查找、排序、释放 [参考]。
下面是洛谷P1996的list实现。
#include <bits/stdc++.h>
using namespace std;
int main(){
int n, m;
cin>>n>>m;
list<int>node;
for(int i=1;i<=n;i++) //建立链表
node.push_back(i);
list<int>::iterator it = node.begin();
while(node.size()>1){ //list的大小由STL自己管理
for(int i=1;i<m;i++){ //数到m
it++;
if(it == node.end()) //循环链表,end()是list末端下一位置
it = node.begin();
}
cout << *it <<"";
list<int>::iterator next = ++it;
if(next==node.end()) next=node.begin(); //循环链表
node.erase(--it); //删除这个节点,node.size()自动减1
it = next;
}
cout << *it;
return 0;
}
1.6 链表习题
畅销书《剑指offer》给出了练习链表的OJ地址:https://leetcode-cn.com/problemset/lcof/
其中这些题是链表习题:
面试题06-从尾到头打印链表
面试题22-链表中倒数第k个节点
面试题24-反转链表
面试题25-合并两个有序链表
面试题35-复杂链表的复制
面试题52-两个链表的第一个公共节点
面试题18-删除链表中的节点
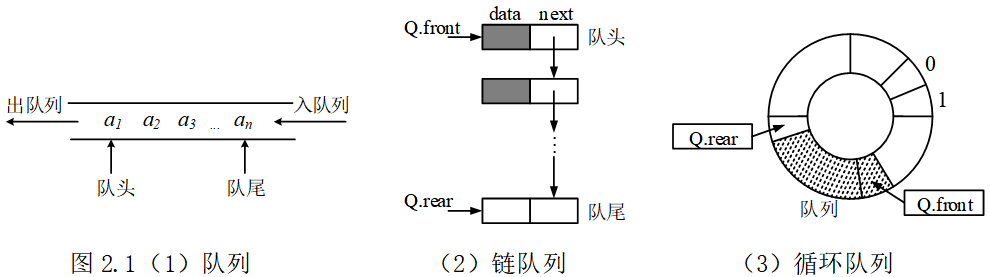
2 队列
队列中的数据存取方式是“先进先出”。例如食堂打饭的队伍,先到先服务。
队列有两种实现方式:链队列和循环队列。
洛谷P1540 https://www.luogu.com.cn/problem/P1540
机器翻译
题目描述:内存中有M个单元,每单元能存放一个单词和译义。每当软件将一个新单词存入内存前,如果当前内存中已存入的单词数不超过M-1,软件会将新单词存入一个未使用的内存单元;若内存中已存入M个单词,软件会清空最早进入内存的那个单词,腾出单元来,存放新单词。
假设一篇英语文章的长度为N个单词。给定这篇待译文章,翻译软件需要去外存查找多少次词典?假设在翻译开始前,内存中没有任何单词。
输入:共2行。每行中两个数之间用一个空格隔开。
第一行为两个正整数M,N,代表内存容量和文章的长度。
第二行为N个非负整数,按照文章的顺序,每个数(大小不超过1000)代表一个英文单词。文章中两个单词是同一个单词,当且仅当它们对应的非负整数相同。。
输出:一个整数,为软件需要查词典的次数。
输入输出样例:
输入
3 7
1 2 1 5 4 4 1
输出
5
2.1 STL queue
STL queue的有关操作:
queue
q. push(item); //把item放进队列
q.front(); //返回队首元素,但不会删除
q.pop(); //删除队首元素
q.back(); //返回队尾元素
q.size(); //返回元素个数
q.empty(); //检查队列是否为空
下面是洛谷P1540的代码,由于不用自己管理队列,代码很简洁。
注意代码中检查内存中有没有单词的方法。如果一个一个地搜索,太慢了;用hash不仅很快而且代码简单。
#include<bits/stdc++.h>
using namespace std;
int hash[1003]={0}; //用hash检查内存中有没有单词,hash[i]=1表示单词i在内存中
queue<int> mem; //用队列模拟内存
int main(){
int m,n;
scanf("%d%d",&m,&n);
int cnt=0; //查词典的次数
while(n--){
int en;
scanf("%d",&en); //输入一个英文单词
if(!hash[en]){ //如果内存中没有这个单词
++cnt;
mem.push(en); //单词进队列,放到队列尾部
hash[en]=1; //记录内存中有这个单词
while(mem.size()>m){ //内存满了
hash[mem.front()] = 0; //从内存中去掉单词
mem.pop(); //从队头去掉
}
}
}
printf("%d\n",cnt);
return 0;
}
2.2 手写循环队列
下面是循环队列的模板。代码中给出了静态分配空间和动态分配空间两种方式。竞赛中用静态分配更好。
#include<bits/stdc++.h>
#define MAXQSIZE 1003 //队列大小
int hash[MAXQSIZE]={0}; //用hash检查内存中有没有单词
struct myqueue{
int data[MAXQSIZE]; //分配静态空间
/* 如果动态分配,就这样写: int *data; */
int front; //队头,指向队头的元素
int rear; //队尾,指向下一个可以放元素的空位置
bool init(){ //初始化
/*如果动态分配,就这样写:
Q.data = (int *)malloc(MAXQSIZE * sizeof(int)) ;
if(!Q.data) return false; */
front = rear = 0;
return true;
}
int size(){ //返回队列长度
return (rear - front + MAXQSIZE) % MAXQSIZE;
}
bool push(int e){ //队尾插入新元素。新的rear指向下一个空的位置
if((rear + 1) % MAXQSIZE == front ) return false; //队列满
data[rear] = e;
rear = (rear + 1) % MAXQSIZE;
return true;
}
bool pop(int &e){ //删除队头元素,并返回它
if(front == rear) return false; //队列空
e = data[front];
front = (front + 1) % MAXQSIZE;
return true;
}
}Q;
int main(){
Q.init(); //初始化队列
int m,n; scanf("%d%d",&m,&n);
int cnt = 0;
while(n--){
int en; scanf("%d",&en); //输入一个英文单词
if(!hash[en]){ //如果内存中没有这个单词
++cnt;
Q.push(en); //单词进队列,放到队列尾部
hash[en]=1;
while(Q.size()>m){ //内存满了
int tmp;
Q.pop(tmp); //删除队头
hash[tmp] = 0; //从内存中去掉单词
}
}
}
printf("%d\n",cnt);
return 0;
}
2.3 双端队列和单调队列
前面讲的队列,是很“规矩”的,队列的元素都是“先进先出”,队头的只能弹出,队尾只能进入。有没有不那么“规矩”的队列呢?
这就是双端队列。双端队列是一种具有队列和栈性质的数据结构,它能在两端进行插入和删除,而且也只能在两端插入和删除。
STL中的deque是双端队列,它的用法是:
dq[i]:返回q中下标为i的元素;
dq.front():返回队头;
dq.back():返回队尾;
dq.pop_back():删除队尾。不返回值;
dq.pop_front():删除队头。不返回值;
dq.push_back(e):在队尾添加一个元素e;
dq.push_front(e):在队头添加一个元素e。
双端队列的经典应用是单调队列。单调队列有2个特征:
(1)队列中的元素是单调有序的,且元素在队列中的顺序和原来在序列中的顺序一致;
(2)单调队列的队头和队尾都能入队和出队。
其中(1)是我们期望的结果,它是通过(2)来实现的。
单调队列用起来非常灵活,在很多问题中应用它可以获得优化。简单地说是这样实现的:序列中的n个元素,用单调队列处理时,每个元素只需要进出队列一次,复杂度是O(n)。
下面用两个模板题来讲解单调队列的应用,了解它们如何通过单调队列获得优化。注意队列中“删头、去尾、窗口”的操作。
2.3.1 滑动窗口
洛谷 P1886 https://www.luogu.com.cn/problem/P1886
滑动窗口 /【模板】单调队列
题目描述:有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1,3,-1,-3,5,3,6,7], and k = 3。
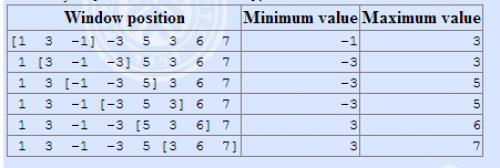
输入输出:输入一共有两行,第一行有两个正整数 n,k。 第二行 n 个整数,表示序列 a。输出共两行,第一行为每次窗口滑动的最小值,第二行为每次窗口滑动的最大值。
注意:\(1 ≤ k ≤ n ≤ 10^{6},a_i\in[-2^{31}, 2^{31}]\)
输入输出样例:
输入
8 3
1 3 -1 -3 5 3 6 7
输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7
这一题用暴力法很容易编程,从头到尾扫描,每次检查\(k\)个数,一共检查\(O(nk)\)次。暴力法显然会超时,这一题需要用\(O(n)\)的算法。
下面用单调队列来求解,它的复杂度是\(O(n)\)的。
在这一题中,单调队列有以下特征:
(1)队头的元素始终是队列中最小的;根据题目需要输出队头,但是不一定弹出。
(2)元素只能从队尾进入队列,从队头队尾都可以弹出。
(3)序列中的每个元素都必须进入队列。例如a进队尾时,和原队尾b比较,如果a≤b,就从队尾弹出b;弹出队尾所有比a大的,最后a进入队尾。入队的这个操作,保证了队头元素是队列中最小的。
直接看上述题解可能有点晕,这里以食堂排队打饭为例子来说明它。
大家到食堂排队打饭时都有一个心理,在打饭之前,先看看里面有什么菜,如果不好吃就走了。不过,能不能看到和身高有关,站在队尾的人如果个子高,眼光能越过前面队伍的脑袋,看到里面的菜;如果个子矮,会被挡住看不见。
矮个子希望,要是前面的人都比他更矮就好了。如果他会魔法,他来排队的时候,队尾比他高的就自动从队尾离开,新的队尾如果仍比他高,也会离开。最后,新来的矮个子成了新的队尾,而且是最高的。他终于能看到菜了,让人兴奋的是,菜很好吃,所以他肯定不会走。
假设每一个新来的魔法都比队列里的人更厉害,这个队伍就会变成这样:每个新来的人都能排到队尾,但是都会被后面来的矮个子赶走。这样一来,这个队列就会始终满足单调性:从队头到队尾,由矮到高。
但是,让这个魔法队伍郁闷的是,打饭阿姨一直忙她的,顾不上打饭。所以排头的人等了一会儿,就走了,等待时间就是k。这有一个附带的现象:队伍长度不会超过k。
输出什么呢? 每当新来一个排队的人,如果排头还没走,就跟阿姨喊一声,这就是输出。
以上是本题的现实模型。
下面举例描述算法流程,队列是{\(1,3,-1,-3,5,3,6,7\)},读者可以把数字想象成身高。以输出最小值为例,下面表格中的“输出队首”就是本题的结果。
| 元素进入队尾 | 元素进队顺序 | 队列 | 窗口范围 | 队首在窗口内吗? | 输出队首 | 弹出队尾 | 弹出队首 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | [1] | 是 | ||||
| 3 | 2 | [1 2] | 是 | ||||
| -1 | 3 | [1 2 3] | 是 | -1 | 3,1 | ||
| -3 | 4 | [2 3 4] | 是 | -3 | -1 | ||
| 5 | 5 | [3 4 5] | 是 | -3 | |||
| 3 | 6 | [4 5 6] | 是 | -3 | 5 | ||
| 6 | 7 | [5 6 7] | -3否,3是 | 3 | -3 | ||
| 7 | 8 | [6 7 8] | 是 | 3 | |||
| 单调队列的时间复杂度:每个元素最多入队1次、出队1次,且出入队都是\(O(1)\)的,因此总时间是\(O(n)\)。题目需要逐一处理所有\(n\)个数,所以\(O(n)\)已经是能达到的最优复杂度。 | |||||||
| 从以上过程可以看出,单调队列有两个重要操作:删头、去尾。 | |||||||
| (1)删头。如果队头的元素脱离了窗口,这个元素就没用了,弹出它。 | |||||||
| (2)去尾。如果新元素进队尾时,原队尾的存在破坏了队列的单调性,就弹出它。 | |||||||
| 下面是P1886的代码[参考]。在代码中,用双端队列实现了单调队列。 |
#include<bits/stdc++.h>
using namespace std;
int a[1000005];
deque<int>q; //队列中的数据,实际上是元素在原序列中的位置
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++){ //输出最小值
while(!q.empty() && a[q.back()]>a[i]) //去尾
q.pop_back();
q.push_back(i);
if(i>=m){ //每个窗口输出一次
while(!q.empty() && q.front()<=i-m) //删头
q.pop_front();
printf("%d ", a[q.front()]);
}
}
printf("\n");
while(!q.empty()) q.pop_front(); //清空,下面再用一次
for(int i=1;i<=n;i++){ //输出最大值
while(!q.empty() && a[q.back()]<a[i]) //去尾
q.pop_back();
q.push_back(i);
if(i>=m){
while(!q.empty() && q.front()<=i-m) //删头
q.pop_front();
printf("%d ", a[q.front()]);
}
}
printf("\n");
return 0;
}
2.3.2 最大子序和
给定长度为n的整数序列A,它的“子序列”定义是:A中非空的一段连续的元素。子序列和,例如序列(6,-1,5,4,-7),前4个元素的和是6 + (-1) + 5 + 4 = 14。
最大子序和问题,按子序列有无长度限制,有两种:
(1)不限制子序列的长度。在所有可能的子序列中,找到一个子序列,该子序列和最大。
(2)限制子序列的长度。给一个限制m,找出一段长度不超过m的连续子序列,使它的和最大。
问题(1)比较简单,用贪心或DP,复杂度都是O(n)的。
问题(2)用单调队列,复杂度也是O(n)的。通过这个例子,读者可以理解为什么单调队列能用于DP优化。
问题(1)不是本节的内容,不过为了参照,下面也给出题解。
1. 问题(1)的求解
用贪心或DP,在O(n)时间内求解。例题是hdu 1003。
hdu 1003 http://acm.hdu.edu.cn/showproblem.php?pid=1003
Max Sum
题目描述:给一个序列,求最大子序和。
输入:第1行是整数T,表示测试用例个数,1<=T<=20。后面跟着T行,每一行第1个数是N,后面是N个数,1<=N<=100000,每个数在[-1000, 1000]内。
输出:对每个测试,输出2行,第1行是"Case #:",其中"#"是第几个测试,第2行输出3个数,第1个数是最大子序和,第2和第3个数是开始和终止位置。
输入输出样例:
输入
2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5
输出
Case 1:
14 1 4
Case 2:
7 1 6
题解1:贪心。 逐个扫描序列中的元素,累加。加一个正数时,和会增加;加一个负数时,和会减少。如果当前得到的和变成了负数,这个负数和在接下来的累加中,会减少后面的求和。所以抛弃它,从下一位置开始重新求和。
点击查看hdu 1003的贪心代码
#include "bits/stdc++.h" using namespace std;
const int INF = 0x7fffffff;
int main(){
int t; cin >> t; //测试用例个数
for(int i = 1; i <= t; i++){
int n; cin >> n;
int maxsum = -INF; //最大子序和,初始化为一个极小负数
int start=1, end=1, p=1; //起点,终点,扫描位置
for(int j = 1; j <= n; j++){
int a; cin >> a; //读入一个元素
int sum = 0; //子序和
sum += a;
if(sum > maxsum){
maxsum = sum;
start = p;
end = j;
}
if(sum < 0){ //扫到j时,前面的最大子序和是负数,那么从下一个j重新开始求和。
sum = 0;
p = j+1;
}
}
printf("Case %d:\n",i);
printf("%d %d %d\n", maxsum,start,end);
if(i != t) cout << endl;
}
return 0;
}
题解2:DP。用dp[i]表示到达第i个数时,a[1]~a[i]的最大子序和。状态转移方程为dp[i] = max(dp[i-1]+a[i], a[i])。
点击查看hdu 1003的DP代码
#include "bits/stdc++.h" using namespace std;
int dp[100005]; //dp[i]: 以第i个数为结尾的最大值
int main(){
int t; cin>>t;
for(int i=1;i<=t;i++){
int n; cin >> n;
for(int j=1;j<=n;j++) cin >> dp[j];
int start=1, end=1, p=1; //起点,终点,扫描位置
int maxsum = dp[1];
for(int j=2; j<=n; j++){
if(dp[j-1] >= 0) //dp[i-1]大于0,则对dp[i]有贡献
dp[j] = dp[j-1]+dp[j]; //转移方程
else p = j;
if(dp[j]> maxsum ) {
maxsum = dp[j];
start = p;
end = j;
}
}
printf("Case %d:\n",i);
printf("%d %d %d\n", maxsum,start,end);
if(i != t) cout << endl;
}
}
2. 问题(2)的求解
和2.3.1节的滑动窗口类似,可以用单调队列的“窗口、删头、去尾”来解决问题(2)。
首先求前缀和s[i]。s[i]是a[1]~a[i]的和,算出所有的s[i]~s[n],时间是O(n)的。
问题(2)转换为:找出两个位置i, k,使得s[i] - s[k]最大,i - k≤ M。对于某个特定的s[i], 就是找到与它对应的最小s[k]。如果简单地暴力检查,对每个i,检查比它小的m个s[k],那么总复杂度是O(nm)的。
用单调队列,可以使复杂度优化到O(n)。其关键是,s[k]只进入和弹出队列一次。基本过程是这样的,从头到尾检查s[],当检查到某个s[i]时,在窗口m内:
(1)找到最小的那个s[k],并检查s[i]-s[k]是不是当前的最大子序和,如果是,就记录下来。
(2)比s[i]大的所有s[k]都可以抛弃,因为它们在处理s[i]后面的s[i']时也用不着了,s[i']-s[i]要优于s[i']-s[k],留着s[i]就可以了。
这个过程用单调队列最合适:s[i]进队尾时;如果原队尾比s[i]大就去尾;如果队头超过窗口范围m就去头;而最小的那个s[k]就是队头。因为每个s[i]只进出队列一次,所以复杂度为O(n)。
下面是代码。
#include<bits/stdc++.h>
using namespace std;
deque<int> dq;
int s[100005];
int main(){
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%lld",&s[i]);
for(int i=1;i<=n;i++) s[i]=s[i]+s[i-1]; //计算前缀和
int ans = -1e8;
dq.push_back(0);
for(int i=1;i<=n;i++) {
while(!dq.empty() && dq.front()<i-m) //队头超过m范围:删头
dq.pop_front();
if(dq.empty())
ans = max(ans,s[i]);
else
ans = max(ans,s[i]-s[dq.front()]); //队头就是最小的s[k]
while(!dq.empty() && s[dq.back()] >= s[i]) //队尾大于s[i],去尾
dq.pop_back();
dq.push_back(i);
}
printf("%d\n",ans);
return 0;
}
在这个例子中,s[i]的操作实际上符合DP的特征。通过这个例子,读者能理解,为什么单调队列可以用于DP的优化。
2.4 队列习题
(1)单调队列简单题[https://blog.csdn.net/sinat_40471574/article/details/90577147]:洛谷 P1440,P2032,P1714,P2629,P2422。
(2)单调队列可以用于优化DP,例如多重背包的优化等。请参考:
https://blog.csdn.net/FSAHFGSADHSAKNDAS/article/details/52825227
优化DP:洛谷 P3957、P1725。
(3)二维队列:洛谷 P2776
3 栈
栈的特点是“先进后出”。例如坐电梯,先进电梯的被挤在最里面,只能最后出来;一管泡腾片,最先放进管子的药片位于最底层,最后被拿出来。
编程中常用的递归,就是用栈来实现的。栈需要用空间存储,如果栈的深度太大,或者存进栈的数组太大,那么总数会超过系统为栈分配的空间,就会爆栈,即栈溢出。这是递归的主要问题。
本节的栈用到STL stack,或者自己写栈。为避免爆栈,需要控制栈的大小。
3.1 STL stack
STL stack的有关操作:
stack
s.push(item); //把item放到栈顶
s.top(); //返回栈顶的元素,但不会删除。
s.pop(); //删除栈顶的元素,但不会返回。在出栈时需要进行两步操作,先top()获得栈顶元素,再pop()删除栈顶元素
s.size(); //返回栈中元素的个数
s.empty(); //检查栈是否为空,如果为空返回true,否则返回false
下面用一个例题说明栈的应用。
hdu 1062 http://acm.hdu.edu.cn/showproblem.php?pid=1062
Text Reverse
翻转字符串。例如,输入“olleh !dlrow”,输出“hello world!”。
下面是hdu 1062的代码。
#include<bits/stdc++.h>
using namespace std;
int main(){
int n;
char ch;
scanf("%d",&n); getchar();
while(n--){
stack<char> s;
while(true){
ch = getchar(); //一次读入一个字符
if(ch==' '||ch=='\n'||ch==EOF){
while(!s.empty()){
printf("%c",s.top()); //输出栈顶
s.pop(); //清除栈顶
}
if(ch=='\n'||ch==EOF) break;
printf("");
}
else
s.push(ch); //入栈
}
printf("\n");
}
return 0;
}
3.2 手写栈
自己写个栈,很节省空间。下面是hdu 1062的代码。
#include<bits/stdc++.h>
const int maxn = 100000 + 100;
struct mystack{
char a[maxn]; //存放栈元素,字符型
int t = 0; //栈顶位置
void push(char x){ a[++t] = x; } //送入栈
char top() { return a[t]; } //返回栈顶元素
void pop() { t--; } //弹出栈顶
int empty() { return t==0?1:0;} //返回1表示空
}st;
int main(){
int n;
char ch;
scanf("%d",&n); getchar();
while(n--){
while(true){
ch = getchar(); //一次读入一个字符
if(ch==' '||ch=='\n'||ch==EOF){
while(!st.empty()){
printf("%c",st.top()); //输出栈顶
st.pop(); //清除栈顶
}
if(ch=='\n'||ch==EOF) break;
printf("");
}
else
st.push(ch); //入栈
}
printf("\n");
}
return 0;
}
3.3 单调栈
单调栈可以处理比较问题。单调栈内的元素是单调递增或递减的的,有单调递增栈、单调递减栈。
单调栈比单调队列简单,因为栈只有一个出入口。
下面的例题是单调栈的简单应用。
洛谷 P2947 https://www.luogu.com.cn/problem/P2947
向右看齐
题目描述:N(1≤N≤10^5)头奶牛站成一排,奶牛i的身高是Hi(l≤Hi≤1,000,000)。现在,每只奶牛都在向右看齐。对于奶牛i,如果奶牛j满足i<j且Hi<Hj,我们说奶牛i仰望奶牛j。求出每只奶牛离她最近的仰望对象。
输入输出:第 1 行输入 N,之后每行输入一个身高 H_i。输出共 N 行,按顺序每行输出一只奶牛的最近仰望对象,如果没有仰望对象,输出 0。
输入输出样例:
输入
6
3
2
6
1
1
2
输出
3
3
0
6
6
0
题解:从后往前遍历奶牛,并用一个栈保存从低到高的奶牛,栈顶的奶牛最矮,栈底的最高。具体操作是:遍历到奶牛i时,与栈顶的奶牛比较,如果不比i高,就弹出栈顶,直到栈顶的奶牛比i高,这就是i的仰望对象;然后把i放进栈顶,栈里的奶牛仍然保持从低到高。
复杂度:每个奶牛只进出栈一次,所以是\(O(n)\)的。
下面分别用STL stack和手写栈来实现。
(1)用STL stack实现
#include<bits/stdc++.h>
using namespace std;
int h[100001], ans[100001];
int main(){
int n;
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&h[i]);
stack<int>st;
for (int i=n;i>=1;i--){
while (!st.empty() && h[st.top()] <= h[i]) //栈顶奶牛没我高,弹出它,直到栈顶奶牛更高
st.pop();
if (st.empty()) //栈空,没有仰望对象
ans[i]=0;
else //栈顶奶牛更高,是仰望对象
ans[i]=st.top();
st.push(i);
}
for (int i=1;i<=n;i++)
printf("%d\n",ans[i]);
return 0;
}
(2)手写栈
和3.2节几乎一样,只是改了栈元素的类型。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 100000 + 100;
struct mystack{
int a[maxn]; //存放栈元素,int型
int t = 0; //栈顶位置
void push(int x){ a[++t] = x; } //送入栈
int top() { return a[t]; } //返回栈顶元素
void pop() { t--; } //弹出栈顶
int empty() { return t==0?1:0;} //返回1表示空
}st;
int h[maxn], ans[maxn];
int main(){
int n;
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&h[i]);
for (int i=n;i>=1;i--){
while (!st.empty() && h[st.top()] <= h[i]) //栈顶奶牛没我高,弹出它,直到栈顶奶牛更高
st.pop();
if (st.empty()) //栈空,没有仰望对象
ans[i]=0;
else //栈顶奶牛更高,是仰望对象
ans[i]=st.top();
st.push(i);
}
for (int i=1;i<=n;i++)
printf("%d\n",ans[i]);
return 0;
}
3.4 栈习题
洛谷 P5788
https://leetcode-cn.com/problemset/lcof/
面试题09-用两个栈实现队列
面试题30-包含min函数的栈
面试题31-栈的压入、弹出序列
面试题58-翻转单词顺序列(栈)
4 堆
4.1 二叉堆概念
堆的特征是:堆顶元素是所有元素的最优值。堆的应用有堆排序和优先队列。
堆有两种:最大堆、最小堆。最大堆的根结点元素有最大值,最小堆的根结点元素有最小值。下面都以最小堆为例进行讲解。
堆可以看成一棵完全二叉树。用数组实现的二叉树堆,树中的每个结点与数组中存放的元素对应。树的每一层,除了最后一层可能不满,其他每一层都是满的。
二叉堆中的每个结点,都是以它为父结点的子树的最小值。
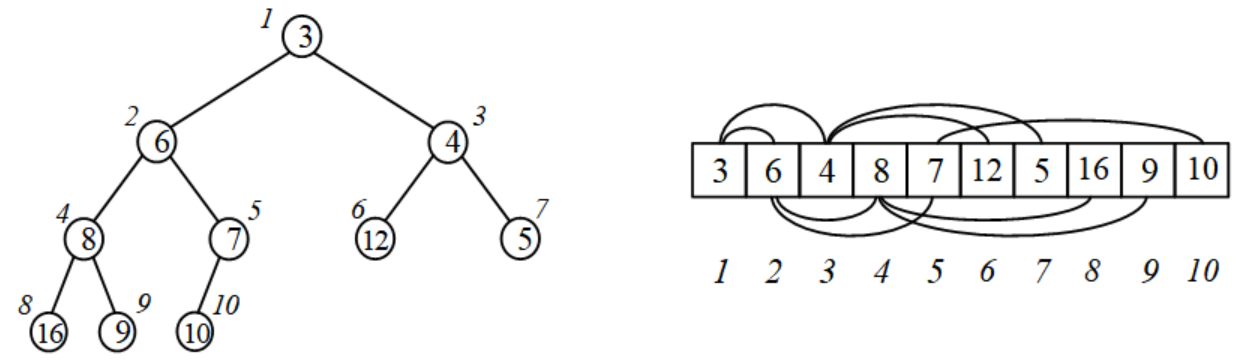
用数组A[]存储完全二叉树,结点数量为n,A[0]不用,A[1]为根结点,有以下性质:
(1)i > 1的结点,其父结点位于i/2;
(2)如果2i > n,那么i没有孩子;如果2i+1 > n,那么i没有右孩子;
(3)如果结点i有孩子,那么它的左孩子是2i,右孩子是2i+1。
堆的操作有进堆和出堆。
(1)进堆:每次把元素放进堆,都调整堆的形状,使得根结点保持最小。
(2)出堆:每次取出的堆顶,就是整个堆的最小值;同时调整堆,使得新的堆顶最小。
复杂度:二叉树只有O(logn)层,进堆和出堆逐层调整,都是O(logn)的。
4.2 二叉堆的实现
堆的具体实现有两个方法[参考《算法》, Robert Sedgewick,人民邮电出版社]:上浮、下沉。
上浮:某个结点的优先级上升,或者在堆底加入一个新元素(建堆,把新元素加入堆),此时需要从下至上恢复堆的顺序。
下沉:某个结点的优先级下降,或者将根结点替换为一个较小的新元素(取出堆顶,用其他元素替换它),此时需要从上至下恢复堆的顺序。
(1)上浮
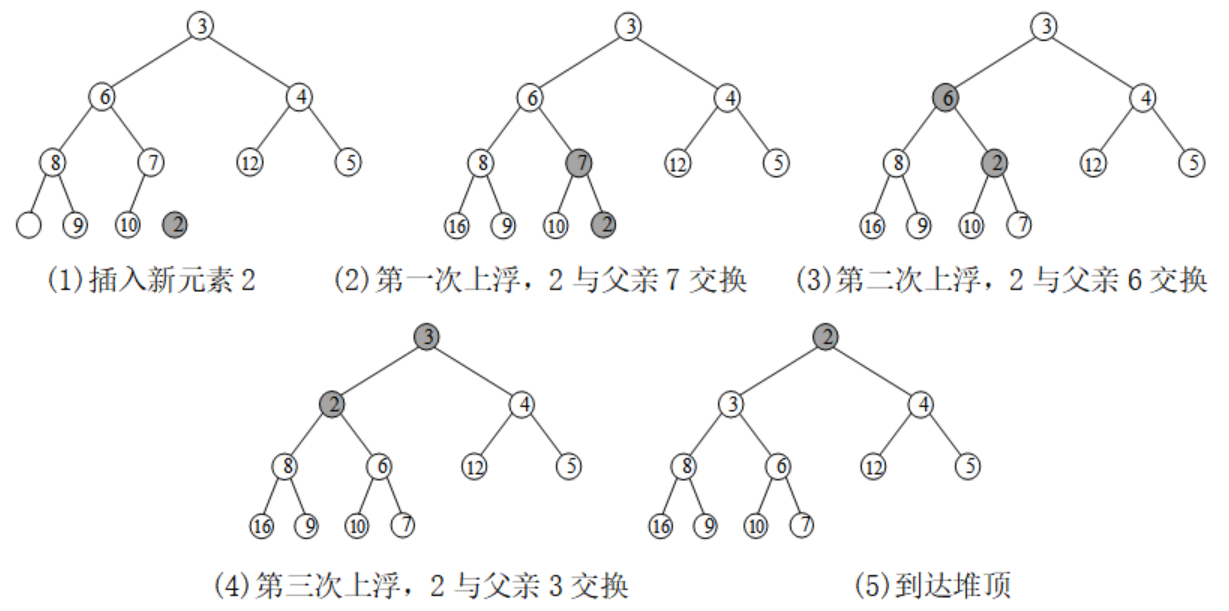
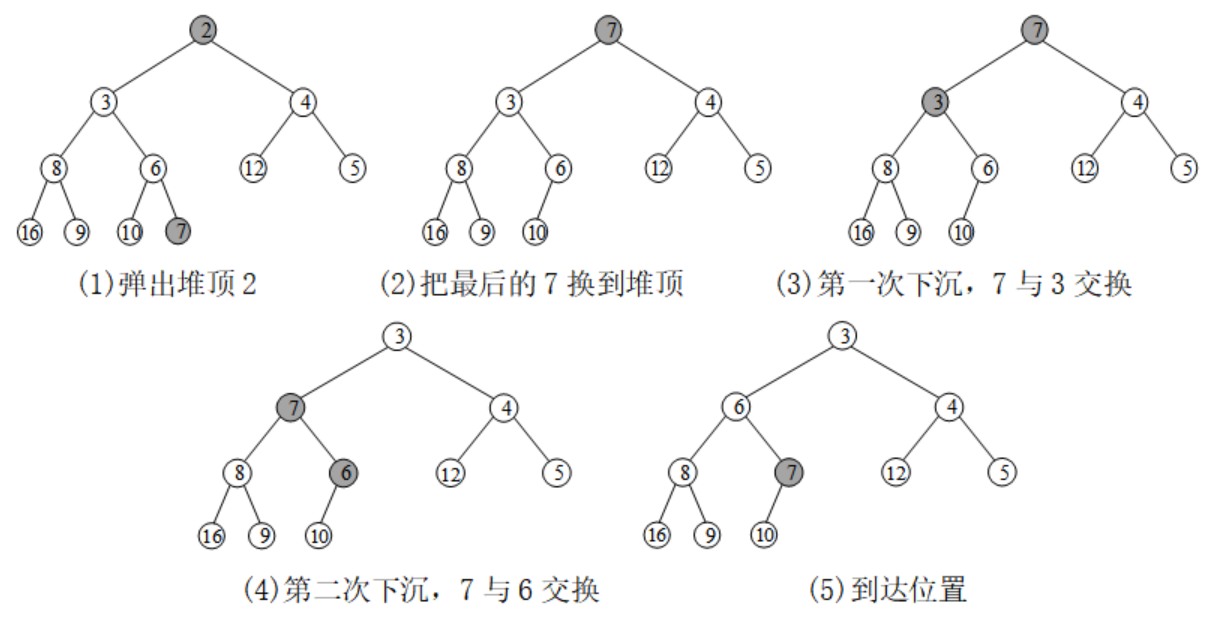
上浮和下沉的代码实现,见下一节的例题。
堆经常用于实现优先队列,上浮对应优先队列的插入push(),下沉对应优先队列的删除队头pop()。
4.3 手写堆
用下面的例题给出手写堆实现。
类似的题目见洛谷P2278。
洛谷P3378堆 https://www.luogu.com.cn/problem/P3378
题目描述:
初始小根堆为空,我们需要支持以下3种操作:
操作1: 1 x 表示将x插入到堆中
操作2: 2 输出该小根堆内的最小数
操作3: 3 删除该小根堆内的最小数
输入格式:
第一行包含一个整数N,表示操作的个数,N<=1000000。
接下来N行,每行包含1个或2个正整数,表示三种操作,格式如下:
操作1: 1 x
操作2: 2
操作3: 3
输出格式:
包含若干行正整数,每行依次对应一个操作2的结果。
输入输出样例:
输入
5
1 2
1 5
2
3
2
输出
2
5
题解:
下面给出代码。
上浮用push()实现,完成插入新元素的功能,对应优先队列的入队。
下沉用pop()实现,完成删除堆头的功能,对应优先队列的删除队头。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 5;
int heap[maxn], len=0; //len记录当前二叉树的长度
void push(int x) { //上浮,插入新元素
heap[++len] = x;
int i = len;
while (i > 1 && heap[i] < heap[i/2]){
swap(heap[i], heap[i/2]);
i = i/2;
}
}
void pop() { //下沉,删除堆头,调整堆
heap[1] = heap[len--]; //根结点替换为最后一个结点,然后结点数量减1
int i = 1;
while ( 2*i <= len) { //至少有左儿子
int son = 2*i; //左儿子
if (son < len && heap[son + 1] < heap[son])
//son<len表示有右儿子,选儿子中较小的
son++; //右儿子更小
if (heap[son] < heap[i]){ //与小的儿子交换
swap(heap[son], heap[i]);
i = son; //下沉到儿子处
}
else break; //如果不比儿子小,就停止下沉
}
}
int main() {
int n; scanf("%d",&n);
while(n--){
int op; scanf("%d",&op);
if (op == 1) {
int x; scanf("%d",&x);
push(x); //加入堆
}
else if (op == 2)
printf("%d\n", heap[1]); //打印堆头
else pop(); //删除堆头
}
return 0;
}
4.4 STL priority_queue
STL的优先队列priority_queue,实际上是一个堆。
下面是洛谷P3378的STL代码。
#include<bits/stdc++.h>
using namespace std;
priority_queue<int ,vector<int>,greater<int> >q; //定义堆
int main(){
int n; scanf("%d",&n);
while(n--) {
int op; scanf("%d",&op);
if(op==1) {
int x; scanf("%d",&x);
q.push(x);
}
else if(op==2)
printf("%d\n",q.top());
else q.pop();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号