线性代数笔记

 

 

 

平凡解： Ax=0中的零解，即x=0，称为平凡解

非平凡解： AX=0, 如果行列式|A|=0，那么A不可逆， 则X有非平凡解；否则，A可逆，那么只有解X=0，即是平凡解。

给定向量组 a1, a2, ···, am , x1a1+x2a2+···+xmam= 0

线性无关：  x 只有零解

线性相关， x有非0 解

 

 

 

1. 特征向量

 

 

2. 对称矩阵   A^T = A

 

3. 齐次方程   指简化后的方程中所有非零项的指数相等 

 

4. 特征方程

 

 

5.  对角阵

5.1 对角化定理：

如果A 可以写为  A= PDP^-1 ，P可逆且D为对角阵，   称 A可对角化，

已知A求 可逆矩阵P 和 对角阵D的方法

1.A-λE化简为 最简阶梯型矩阵

2. 令对角线值相乘 得 f(λ) = 0， 求得λ的三个解  λ1 λ2 λ3

3. 将每个λ代入  Ax = λx   求得x    再单位化就得到特征向量  u1 u2 u3 ， （如果无法得到3个特征向量就说明无法对角化）

4  P = [ u1 u2 u3  ]  即可逆矩阵 ， D = [    ^λ1 λ2 _λ3  ]即为对角矩阵  

 

 

6  求矩阵的逆

 

 

7   阶梯性矩阵的 行列式等于     对角线上的数字乘积 

 

 

8.  向量空间的基

向量空间V的一组向量若满足

1）线性无关

2）V中任一向量可由此向量线性表出，则称该组向量V中的一个基（亦称基底）。

 

 

9 正交矩阵    A^T = A^-1   或  AA^T = E

 

 

 

 

10  

 A可以正交对角化    等价于    A是对称矩阵

 

11    二次型定义

 

 

 

12   主轴定理

 

13  正定矩阵和负定矩阵的判断方法  （特征值）

 

 

14   求z = x^TAx 的最大值 （xTx=1） 就是求A的特征值最大值   再通过特征值求   u向量，   u单位化之后就是我们的解。

 

 15   如果x 和 u1  ....uk-1  等k-1个特征向量垂直，  那么最大值就是在x=uk取到  λk 

 

 

 

16  怎么求特征方程

已知矩阵A    将A-λE  化简为阶梯型矩阵， 对角线相乘即特征方程f(x)， f(x)=0 的解即为特征值

  

 

 

17 

 矩阵

17.1   矩阵的转置的基本性质

17.2   矩阵乘法性质

 

 

 

18  A的奇异值是啥 

奇异值就是  A^TA  中  特征值的平方根

 

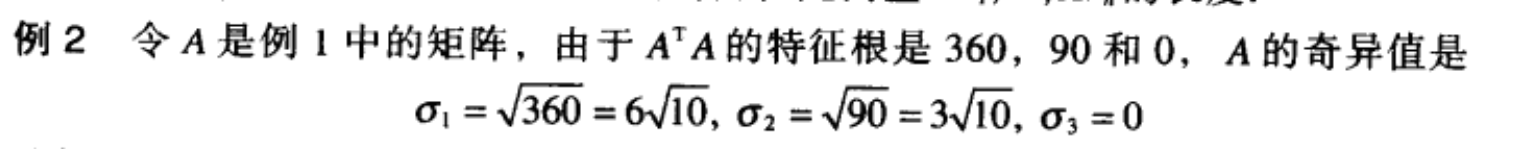
19  奇异值分解

 

 

 

20  协方差矩阵

 

 

 

协方差矩阵的含义  ：

S

其中s13=0  说明 x1 和 x3 无关    tr(S)=10+8+32 = 50 表示S的迹  , 即  总方差 

 

 

21   主成成分分析

 

 

 

22   矢量积