平衡二叉树的旋转
为了了解平衡二叉树(AVL树)的旋转方法,我以用10,35,47,11,5,57,39,14,27,26,84,75,63,41,37,24,96组成一棵平衡二叉树为例。
旋转方式分为四种(LL旋转、RR旋转、LR旋转、RL旋转)。
1.由于节点10的左子树高度为0,右子树高度为2,不平衡,所以旋转。
由三个节点组成的子树旋转,结果则是中间值放中间作为根节点,其他值放两边。
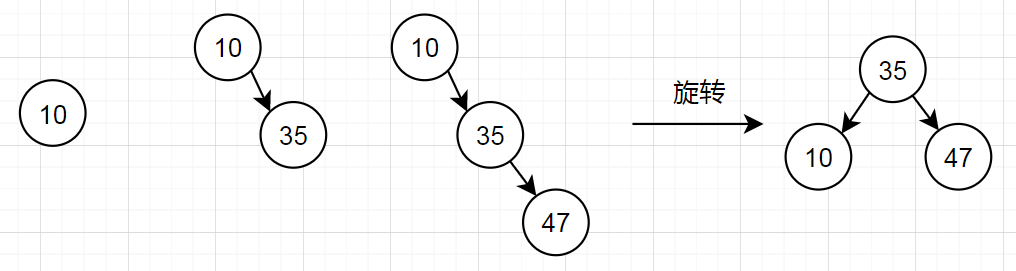
2.平衡二叉树允许树高差<=1,若为2则旋转。
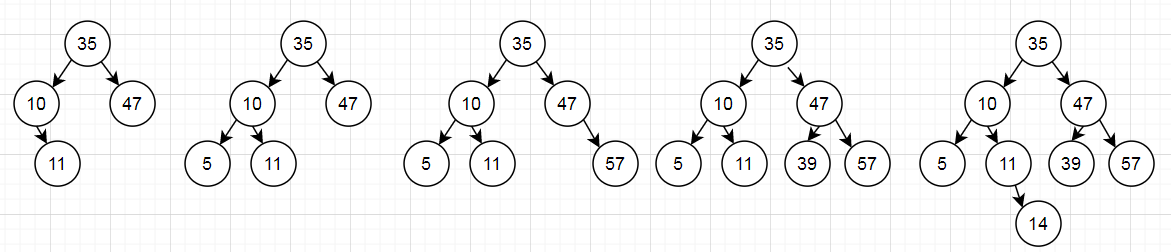
3.由于节点11的左子树高度为0,右子树高度为2,不平衡,所以旋转。
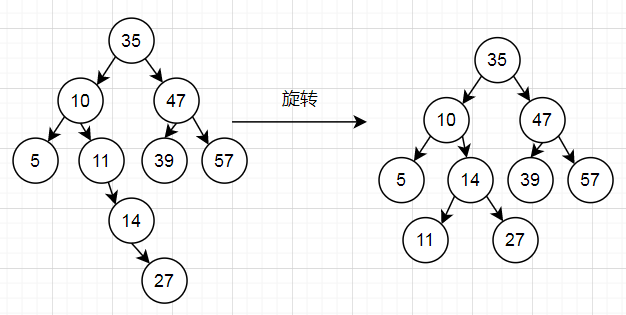
4.由于节点10的左子树高度为1,右子树高度为3,不平衡,所以旋转。
由于是节点10的右子树的右子树插入节点引发不平衡,所以对节点10的子树使用RR旋转。
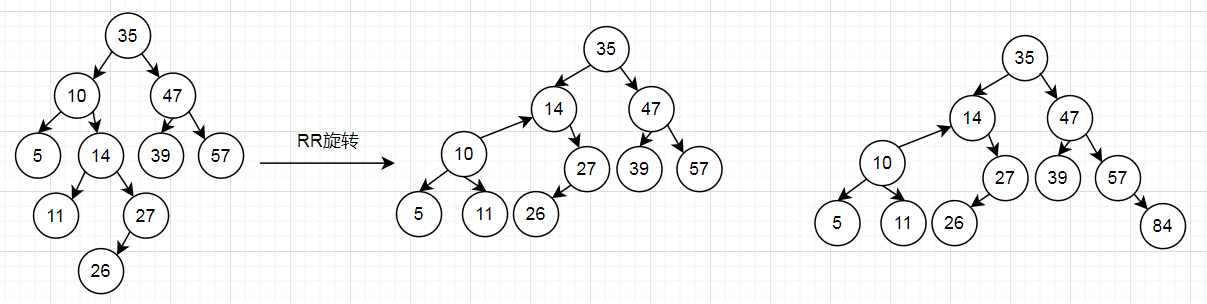
5.由于节点57的左子树高度为0,右子树高度为2,不平衡,所以旋转。
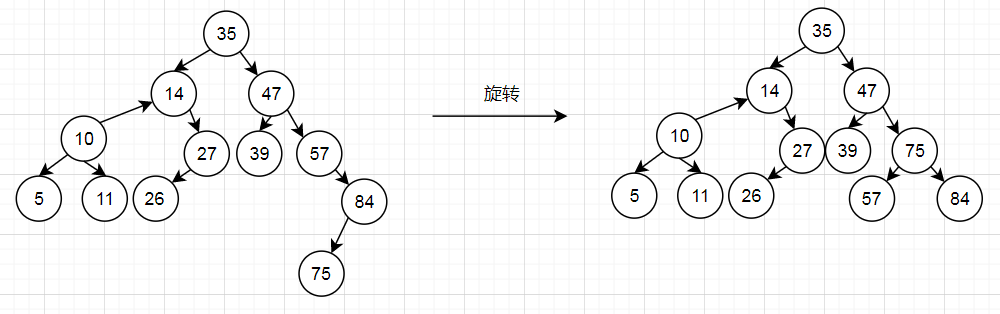
6.由于节点47的左子树高度为1,右子树高度为3,不平衡,所以旋转。
由于是节点47的右子树的左子树插入节点引发不平衡,所以对节点47的子树使用RL旋转(先对节点75的子树右旋,再对节点47的子树左旋)。
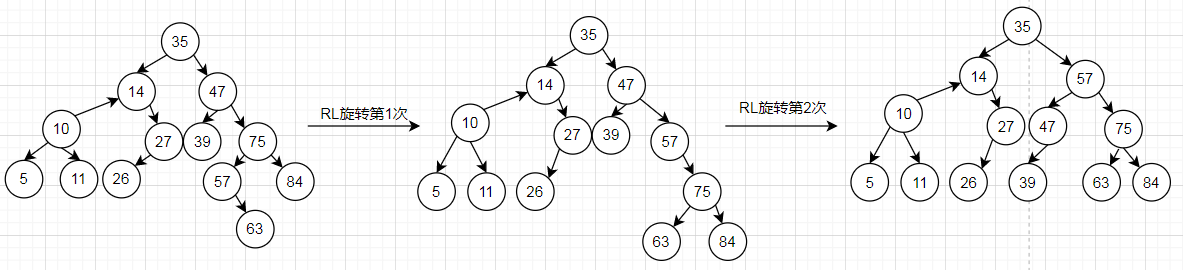
7.由于节点47的左子树高度为2,右子树高度为0,不平衡,所以旋转。
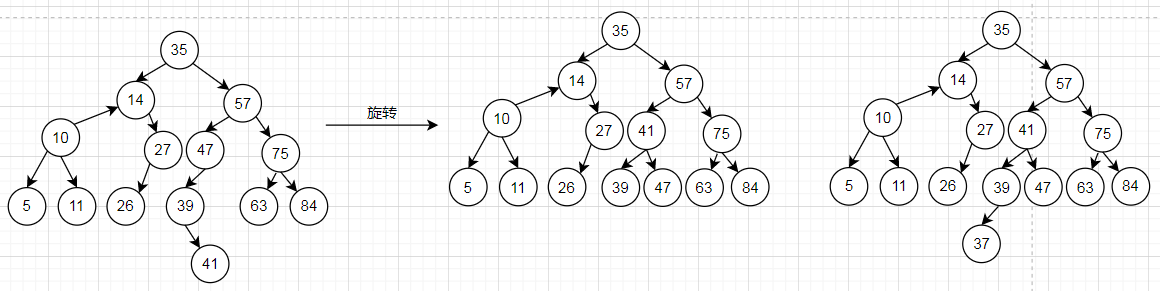
8.由于节点27的左子树高度为2,右子树高度为0,不平衡,所以旋转。
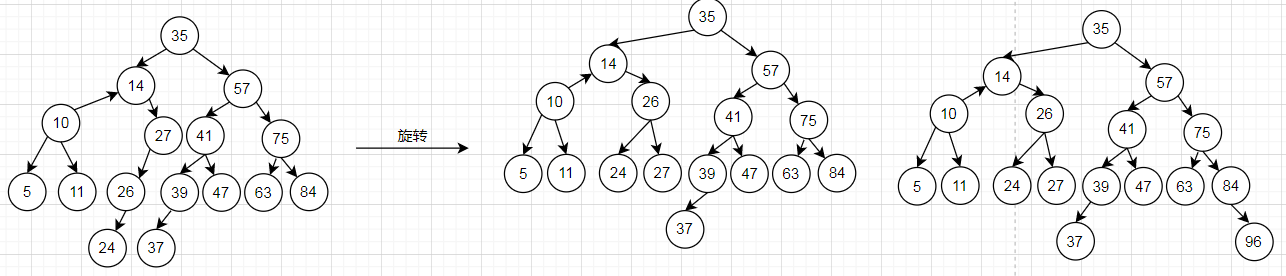
最终得到平衡二叉树。
AVLTree.drawio
<mxfile host="app.diagrams.net" modified="2022-11-21T03:20:58.663Z" agent="5.0 (Windows NT 6.1; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/104.0.0.0 Safari/537.36" etag="9n8OJz862UM2i-7xMxan" version="20.5.3" type="device"><diagram id="q5KKAd3LWqcQheQczGw4" name="第 1 页">7V3Ldhs5kv0aLcWTeANLy3ZPL6bO1OladPdSZbFsnpJFt6zqenz9JC1mShkBikgogQvKmkWPRVkoC4jnjRsRZ+rt5z/+5/byy6cftlfr6zPZXf1xpt6dSSk65fv/t/vkz/tPjHf3H3y83Vzt/9LDBz9t/loPP7n/9LfN1frr5C/ebbfXd5sv0w8/bG9u1h/uJp9d3t5uf5/+tV+219P/6pfLj2v2wU8fLq/5p//cXN19uv/US/fw+d/Xm4+fhv+ysOH+O58vh7+8/02+frq82v7+6CP1/ky9vd1u7+7/9PmPt+vr3eUN93L/c3878N3xH3a7vrlL+YE37390f/v3P3/+j/709x8+/+uH//vp83/O5f0p/728/o1c/Ne7P4c76M/pr7v/4uL3T5u79U9fLj/svvN7/+L9Z5/uPl/3X4n+j/vD1rd36z8O/ivF+Lv3QrPefl7f3f7Z/5X9D6j9f34Ql/2Xvz/c/fA3Pj269uGzy/1rfxzPfbiQ/g/7O5lxP6q1+xFiekESfEGaXZAy2AvS0wuy4Aty7IL49dxcvdmZqv6rD9eXX79uPkxv5Xb7283Vevcf6fqv1n9s7v61/87uz/9+9Od3fzz6S+/+HL646X+Rfz3+4t+Pv3j4oW9fDT91/89cXzH7SF6i/1W2v91+WB/XorvL24/ru2PCxF/20dOZyNMNn92ury/vNv+d/nNj77n/L/y43fS/yIPlIaZHWCIS97/m/qceG1p6kCcHCXLQ/T2wg76J1/hr50tcaM1mya4tmzVcRztGi7o9tNES4tVqDXp01GqJLv62dcyWlguZLe2wZkvwWFQ7rFZaciMdWi15OPpMtVxQXQZxOa4v8tXNL6EvPPSuJAywpyO5j8t9Off0OaUfzvCHe2/PgjvzF2fv/dnFu7M3b9lT9mbsbvp4l9ebjze7l+1fZ33bf7AzdpsPl9dv9t/4vLm62v34xe366+avy5+/HbV76C+7X+3bL2suzsy73Vm/3W2/3oMvu6O/3t1uf12/3V5v+3Pf3Wxvdqf8srm+Jh8tYGTVcB37x9DcxsZEqpyNtex10JCIj4srzAvxlBYcPuvBFv45/dVhN8RTMHAoo/X0htAyNAStbUYy+7c6HskEpDvUB5Cuue7Q2Kls+LruUC4exwy55vDnGbmmAOWa6SJnkSKnCJIzgq2zQzAzPShUljkegqFxfTu92IA20DwMAjt5IjECXRqSPAwCO3makMJlyDfs5AcBP2px798ZZXEFEfvx3LkWl4PwlU0uj4m/PzefLnQGKXTnJCLMDi3PSWImK2Nkg2l77OeHt2qC3wBPVVUEjFpILVcmWTGXVDGTqGIKWrahvjpXwwSFs2trWHNwmaBVG3QYpJrDy0SYmmV4LK14pIiu/UlyRXApWjx+WtDoqlT44v6hUUZXErnPDqYVgVNrB9OaxzVLee3TCabThQ6KmRFPnx1LU09fO5bWnBMEjqWFI1qIDqa1LKaWmGBapearGkoMYM46V8ckkaja0bTmBB9wpNhavjo4XqTngyiYasiHnWy2qpur+6iuscKPbq7wo0idG56t6uYqP5TRhpeilks/OtnoQks/lN+Rna3qQA6qna2+ln7mCB209CPl1B9lp6vSkYMqu/rhPtpJVxXp1IDH0qZYlw8oXdWptR8Drf0wb53dskN7f2rrGMc7wH101OjAVWzxjh1oupquYLIlJ/YMPIgcVFvBONphwETyTjamYcUIDCfUqqpTSyEG22Lv1Cro7uH/pq0/fda6GsbDzO/GM6vOGeuM1r1/pVLaqZUzUqveFAQjXefrqnFzJAlNgW40YGCaI0mYQUhagZ1McyQJo8gVwaWoHNKwcsE/dgirToannUL/xY/r203/m+26M5c2+SbZ5EMpF5ZoUTaIZQ05qDKINYSQ3zWIlS502DYlyvPJTrApz6dy/G+b41xoT9QQHf9bjkEsZvIhIJZJBYotlHPBfH92+ymRqNo5tm2Nc8GMDlzFXhbnIl3BoJwL6sTyUWIiT9UVjCM0YBDLEAAer2EcIFhIw04IxBoC/ON6Ca2QGi1WVDWfAVwZo9oFrmwElQlY1W2NkGgXZ7rkxJ8Pynv/Q02rL5RVIwkZJn/+G6Wl1Xarzc15tXREAxoOHNx8O6Cy9Y113jmOMIBBZSeYcwVf0eIIw4JWdxDxo1bXQdECR+Q+Gwb2Ctt55xogdMBh4GShs9ABaSzNy3X1ljL3Krt6xwEYMAxs6YQQdBjuXtociyG8O27YoZQO5q1zdcxZLErlOAQDDhVbowu7YqtMIDBwuoJBa5nUiWUrGJWn6grGgRIwDOx0Y2xhV4y+ckIw8JCRHtdLKLHFCbckDOxkaBcGHtp/24GBXdeY6vomemkagIGT1ddDe3C0XahFwNDJvZXdqpdM8IaQvBGMEz5s3i+P2cCdpE7VMgl1kjqsbGdtJ3p36QIVDGli352fOXYrFZQKXnopfCAENa0n3x3YCLXUMwLdgKn/00dQQxMfTDs5cgMu0ripBCmBviEOTYBrNIKwuvFCtDg2saCx9qldkx6KNAgi93qQ+9ldk5JIhyUHlba55SgZp1OjSRc6KH48TsAahE5mCh1dAeUqy1yEjYEt0ZB+GRXAJjpwEGEprcRUaHxyDA6tgjJfna1htAOrsooFDrGgV803pmES7/cQ+hWg1BbqwfL1i8ImldUr0gcDzjIIwxKvYMUaYU6oPuNT22cCtH1GCPHUrIk+Y82u1QhJKPtyerQ1k2IN+aeXVuMInIKt1YiuNTUu1m1zYrWadFXGrqNijiDXxZ7TSZi1fSyHqcDFGor5KLRuLo/dwB1mKtEoYDcNavVErUZ5t0StRphpNYbMV9OdRRZrAgdxJBponxos7cD6Of6DXgyME1JnmgQojCMJfU8Ny0bmzzQkPjCQgwormegiQ02wJVHpacHCoLVMsjtCT+GnWY6E3xEHLNBj+A25I7wcNYBYLGirR704aqz30oGy1ppoi5Ykkkke3uGISLm6IZHoyjXWnE4xdY7cQcFo2dF8LlPuWPnQ15a7yMxUbEGVLgfTGm7dIy0V2CsiUqM7+BWVmwiKcYCp9Oq9cLRiiNRShkjWNkSCJ7zgupgi2AxeywRP6RbSshMqjI0JyXHdFNDeB2XMk6Uxa/LHsFv3RBuTch5YGRMDn7Gd0hjdI92AJpebb3FatbE52iyR2jzm+M/1tMJMD6rvaSO9EtjqmOqa00+eFoFLFEq1lhaJYoMKMKDXoAQJlgjaQKDJCA9lMi2RoczKrrYleu0gmCV3HVTuJHFcRmTKHTP3levPQjQwAGJJCUpHKwS0C+XlSJDkaMUzJShVHmDx79C5PyLVYiUy09fx3/TEWcVfMIKlvLdnwZ35i7P3/uzi3dmbt+xN+/jtbvqKl9ebjze7J+6fabeA6GIX5W0+XF6/2X/j8+bqavfjF7frr5u/Ln/+dtTuxb/sfrdvv625ODPvdmf9drft/856f/TXu9vtr+u32+vtbrHRzfZmd8ovm+tr8tHZ86NL4cmLmIcXOSJf5QLMQafaYTBoNbVfg07AYnDJcQR0V7ebXpGEXxFPd+Ft3eSO8GK0ePU51Z2lhDcyGSKS0PBGENkfR8HN7+wmAuLIQcWdYznq/gklZjPkTiLl7lwRuaOGIhmaJO7N1xa7CG8fTEYI05vVcEvdEmQCLBsMv/Zx3VTQAj3VTZOrm8qupHLWehlCkN5PVdV2cqWt1sL5TmtjaidTHFBBN7UqorkdWnOHk7/v4r1MBjsldpyD6J4q3vch+zP6WuVTfa3GKWT1XnFcBFy9D81pMscllvLBJ1a8T9dmhR0eIbRYxg2P41EG5Ll2jKw44gOu3pvm9JMjPuDivW8tjVDF2g0wFTCVnKorbAVMTCXB5C5okpYcVHlBk1CvENEsuZPQrvOpsDg6PDuZMULsGJ3mXVzoXhjlaPjnJ5gtaJ/dSxGf1hp5BAFu8aFTZDSDhV4RlRnHq9J1r2iI3b5zx5ee+UFxHDXFbWzIBG08OUdXRlgtD9jBXAjVkZR6wGlgmml5SIqe5hCmg3eMhN8Rj6DAbAgtyR1Z+B0tXmNb0vLa1GlyArsBXhPZt4Psz44ayf4448hBxW1vA83NLaC96ZKH3eUoh2VNIx8iU/IUJbPpypLneKwJJkQoYeJ3C7PWQ4Hsu9fO1E0UwmNnpxDtNNnaacyUEjEVTCGQjIhhnlA7jAhNJjzYDq65xZqgT4kRMUTkCV5VIvVWy/A0IyJkMyJ6LX1inIHxEkmIGMYRtUOI0KI5TS43vezEGBEztBnMVZ/KULYXplvItK8dI0cmmIHHGViCjMERDcdRH/Q4A0Zghd9RMWY1prbo0rN1KE5kFLFEJtMSGZIBmK62JSqHE2Fmdu9zSljthrgWJ3IzRTU1yAwQKi0ZnuM4BWxLV1ku2kcCl5MgEi5ZW1uCOMoFnkHqDugUzIEPuFI73AU14MXt3FG5uXMnRF5wyUmah0IuisxLccO05tkAC5mXYg05qLj5WpwtmioPsASbTNSwsls9As86kfeSdK3IkWOLvytPLP/xj+95jkogqOiwCe2R0Nm6Fp+ntWDikKGaAZ/2GNkqDiYOWUfkSKHvKLJXHEwccrQC4eB3tHgpOtXLpcQy9y+I8oeOrFgzlPydzMSU5Nlrz89tYf93C6WO5IWLArvSzRA43urMqYNj1DwilbUlL9L7iaUDmaDjd4uzwbxc+31qp0/UTtlBC5FUO022dir9JB3IIelAkXXhYDqQo0OjBFxzi3WUnhIdaIizE7wqtDjjOr8ixr8PwLMpQG6HYzxBAYJuNInsEwdTgMY+pna0t9xgshOjAM3QYGyDhqHs9tw9AmSeqQ6142KO34ApQOOEj1awCRlZKA6mAFk7NfJwGyYjK7OrRyCLWqLUDH0vHShL5EkfvKHj/JOxIUsOogsGClsiGVkoDvCCS8qQh47PtMS1uNwFz1ZMDTIDgYpLRpVmh3oUoGR8AYz+LSdBJFyylVeEy8iSeWyRahxe1Qr4JyNb1MEUIEsYaA3c0evgrkfhcEJoBIVZrJry5N2wXXW2+aKEe0sOKm6+OIjisUmaI9HiONQFp5svrAdhAAIStAzbg0DSdUunKaZPOCN5P53vWFzLIlAImO4jVtOCvUdPOZORXfNgvo/QltySU/Bb4mgIenGSY7fk4Le0eMa/oAEeJf24ARbYoRBM/n3uhG4ZmJBUntEtC253P6VKyAzpk1D8UUkqfDpT+IR0VPhqRwCx9e5YkpA1h64XZ7XLDSw4KQ3tkisEEtwKStUqW0M7s3KHFyl5gVykJAUHZ8A8oT4npdor4NrbwBhwOFNotOoJsR20CVf4bqUPDw7qQ/j8VUqhTy4Pr1JyHrlKSQqO5oBpQ8I2qMxNTE1owRnPUGjsTkNHIZ1sb9z/KuQoGyrHy8OS3nbIQ0Kw+4XDHJKDQWD6kFCqOVs2mK4Xgt+PupGQHmDhI0/9msttL1OKHUXXnRS3SOXgIwyJaJ9moqTD0RcNuYvZPatlUMdXXDaKtTdBaERzAAhs++piMiQki8FdbSGKdCNBfTmLAvEIoeRIDJhKFEJ7l1QMiDklLlFyC/5egmBATKepEetygRdDj/K1oVLJ0RUwn0iy0NFridbQYugKJiMRqVNN9/IB0zWWwtOmqHTmOgNbKhOPB+l8JEMOHS9MaVY+Mmaprp4pjo9U94SL+rTk8QEKGpcLwkF32bQRMp/G1iaNKMkkCMzc05pBIUOXL07PODYCpu4ZTXFIJ+G3xFECMHXPOHZLFn5LxUggmNgoeRn5Xj5QNtuQGZaMIpUcGgUmVMOc5mpWu6VuGmDtMl32NHST+W6LESWaEpFJ5vpLmgM7XVv6OP4C5vppy7iUCm7ny40mOS0dlck6Cs2duY66bB3t5JTtNxVN0SHJfopjM+C82naMqtuhtVdz9GEh7T0lst8Q0SfEdthhm86tNJlab302wW83+MscHAvmvEDy+zTHfMD8PjpMsQHt5ajGUr73xNh96RqsoVwaJakPyPa+ytGjrK8cIevIyFxslcgwQj0eCdEcLwKz+4zq2otEXhhepNNzdiheZD2zSCbTIjnFjupqW6RyiBGI3XefV8KyReZkgsiUDs1YXgwcKi4dVVqb6vH7ZmAOWFxwOSkyLIDytrYUccQLCyxocVCzcO6cwy9ghp9mowvwt2SKwS+nRPHT6ckbFn7pKFsodJm8I8MH91TedyINB1jAFD/L4kc8CdcUg1hAZezklgADBUo0T+SHBT2zA0/DjtLkqOK6xoES8OQB46bj+RrQtGLNNxiS3wxNgwbnRtMZvrmhOV2bUZsuEtlR/UwJSpUH1NvJYQj9COPlNmb6IwcVf7tIW+b3u+lWDf1vT7Sox8SqmHVW7Y2+VFO6gegk2IOpBidfkgHHwcDviGcd6LmXltwRut1BLT/1EppzqORJhQo8J5Noi+hyubPS05Mq+1P1OiVzruxhW+BFIAKTO2JDDBX4wZxV7n9X7Y3IHDAcdrc4C/86IXMSVSZoJ3RCJtHOkKucQU636FIvoZDzMVVkPiaYMjvuOHi4Ibjqvo7HfBTGJ4R02KkM1q7C4fGYfayfPx7T+elSXeplOuR8TNXgfExDWWctqPPrgMz5Ko0dkOmJDuc643NFOSmVI+X2hmOGKaaGh0Ikh4vQkzEJNNuADRtM1kvBi5IHYypw9cURA0KnWiRXXyQ5iMpKcUv00oZiKuxQTEviHJE7wtnSIgd1dsUl42WNxJyDOEDxwMUkSAgac1eeAa6aG4h5SKdwDry5cZjeNndHr9MwH8XDCeYLiruEaausEDIXZdHkpM5VRkUbHIUpqUkf1g3jtPNlTcJUyZMwFXYS5rkkkiAyCemaZP62LhtdRcZgghmyO+i4OT17YZMwZ+gZeBKmosIQcrkhwrOjapNDItMwBxIUrNBHSqECvcdaRYZhnrRLG24qQdUk1KU56tNyp86ey+lJDJ8rrmc8r0OTZimuMAYMOD3jiR2YNauHZHeQGw2/I56DgFmzOpA78vA7emEpyKAXCfYamoIYoi2ioyP004fxE5miU/1L2+ty0/BOi5aXLnr3VgglekpTmJI2USenvwRmqp7/RsbdgVmzylGcHL0nUxWcd3da+pmcNRtoKE/1M2SrpwhT4iyRTOmQvNnIGDwwb9ZEqHZ47a1SSj4B7U3d/qIMlMSgg3qSO+tN/uRZMsW2fn9UZNwgmB6rnWM6K9FJVRvz9E5LazW0VWUcCvxcnysDOYjOOiquopH9C9jCq6Y8PTjoEZlFB+bHajJOpAUj9sKQIZ2enkORIUsmygeXCwyRDs4gK5uignP6Ts0NJqee4EHrxHsJoTKFT7EexMqT+lRkUl8B+1WPgztDhrDw4mIypElQJjpfW4YkkyEsRKHY/B44QBGZ0oeeWStoMIW/pAbG9OF5uDodw8FO3hZEy8TwXLNNGGtFceSk4iaMQzZgIq4ZmrrH2xVw9SwG2IByndQ1GnvxgMUKjJNNu4ln7PWZnMT6m4vrGcddwOxAw6wYXs84poCe6Ms2pjbQmmwXT11AxgWaiGgy0+uBHTvfi9PCC6Uxl7YuA4X+pTiowRAkJLPgSPAFydDi49NSJQL1esbTO1fjKujZaKo7flbxF+Rh6j/+NzLw+b3b/e+bt9+GQe/+xDlRL3UGtPHUm3fjMz0SulDXn0dqclhGuxN0k0p/US5yUZUDn8j4LXDXe8f6jlQD98TjaDCz3UuKuQn8NbnF4+jTZD7aZNzNYUufQTKrpF2ux3aeUoOCYYeVdtkD3NcOQ9lFMl4b85GVdfV19PYkVjiuqx6aGXFdDc9QVWtW7gmmsgirgGMqD5F/O0xlz0xbA4s8HM9OwORQP5japgxduZE8J8aKsckgkIOO5TGersJ7hqmziq2dDfWjEp5ngUmizrEtoa6BBILnWWCiqAuKWf4GMq1hRsBLwaddesYE7TYJmpkmm22aQmCHieqmyZfL2U/NPSZnAvdJJkoGHfNou8F12amA5sgk97bFpZCn7QXsWT3y6AxZgiJAC8sSC9x2gxCry1JkjTE0hrC+SQTI8zQbTCR1lgdbLVxUS3uwYGRSl5w93gsWzKRZpm1C6FyT5kVEd9lpxU0ah3rApNJApuC0oahNQD2LKp1OVjooZGMZnPCYCDA7jpAMnDDVyR+eYzZggql3LepccxRTb6al8XGgIuyOQrEcG4PW+HQgGRwK8AEzIdsqecFP09XNUli8bpsqGahXHM9ZgFU4Ds8DsgoDz7ueZBWK749VyJ88SparyyoMLe32AOKk6dbfQrF635t621nbCSecC5quMRYm9u3ZIH6nV6L/8eA6Y63sQsS+iCC1MV4HRRcfFLc1PIitHnk8yCwM2U+uLvlXicVKrI5smVrKyq52hZtHUrvq1BHJ7b/4cX276X+pnS9FZvfg4cl21QmtjLRGKOGJxPR56MqKEITvc36hcgcrmz7HV64PqY0TSolACM5CqpX0NljnjVem03XlUvGoDT0lnyQj42uj8lytOFAObicQigSSAg0G6Mi6BXAvQWTluURv0tORhQtL+YFTirZHnTrqIzS2c1OQIeeSLvBMXwVKSKSy8tRVHdljAe4hIHvPeqsGhn11uT0WJ6aeqSGcxk45pOopctXTkxnnJEeRVgKHnOvIbgxw64Bk5gxftNGRPQ7g1oE+baAxCN7IFdzkcFrcSJ08DFFjB2qe01ambDt3Tif/sd3mxW0Zr/SAmwbojFGJ7oHSkW0N4IYBQYch4lOpyBaBhcwYpPyskwci7cUDVrikOyJl9rQ1SU4Slcet6dcVC/MjfuzGO0tERrlM4aPLOFlmX1z2ikFBkOaAOTkjtuV8KQkSgp4ka4sQh3TAHeXkQvC5TqT1EtsN4F1rd1RwwcJ8F4hqBBhj7gTzha2mUx2jYFSy+aKpoOoqw1qR3Qpg/r9UrFWnAf2UxfQTw/8f8czjumawuAuNEXNJAJocJCpvV9aR9Qpg2r/gIwgaUDUOvIBp/8LzKrbEQ+2RfQAL2SQM+GLSvX8H9f5kfKzK3YojFDlJVt6Ko8ttSzitWmu66CloM5wUdiUe8zRJ9iuNn34/TzCldCt7mMcpnVl1OB5nZD9DdbsHZx7PYO8YLFT9KrL9ExQjyzdHPZ6TWEAxyHMhupX2xmqntLde0AUBSoeVeD75+LxPWVZiN7FWS2+t7xhCtxuZiaMfRza5DCQOGGuUMzYGnAIWbdtyCB0KARDJigpF2wQHhKQnpySH3J6fpchZpRUOtxMIFgPQeo/MXcquzLGTir+e5K/HO2zpe77YdlpP3yOycismWQUNdYTcBG6nofUC+UBJxPkzDrOBO2o0ZfwK28A1cZANHB2Zjrsw3cBFvUJJE706HlVhZ32OM7sfUuTsUWZsI5rwtQeZ6dhmJnBrTUf5+T7g1bQcEnFaaprM9HTQ1ZdMTcUz1FTLaYcN9SIWuJtDRzZhgRtsDDVrYzstTH0dRyHA7TUsahtJnLhLKjYU7dQYxTa5SOCgJVXGBH6GlRvB/YfxDtWDkdiuMCyrStNGX9nhc4bIpjBwj42mgzBbSK0iW6sWsmcYosegHQlWCcxSZ5SxbKtkHT1L17dK5aaNn5pfTI7+LXjxPauD5Uf/gnoA7mOLS2AxkAjTbzMji4SCPYvKEY3VVFdfjjjYg00VlW0Q64nshgM33mg6JLeJa2pp4Ays98almzJo8+lIW3ig6YhsUxao1gZ2VmlTFtm3B27AMd5yvgVeTdtYJ7do9JA67ngvJDAMmmEHMmSjM4EOP3HsrOIqx9EZcCOOoVPJ8SBqbNcZFpsxER5YhwbkI6vOFrJKGGzGp2fGUFLgOMVzDANEtk3StB9c2vo2qaVNcEBkZob8GaT8mV5EIm0LD7BxdN767MHVvnuyq8EE5ED1yO646rYP34iTTvjxUDT7VWLPdck1fq314czILiRSLneCZx6tAPBknqzqw74FdgD0afXKP94BIMl/xnTIJQCRnYDg2e1GcBgAn5WUw+pQIEAyRQO7qUNHUCFrckNuo/hpgp1WWOmM5JASuFVA+xUtFGv0Xgkz6Fg7rQK9u+D3JOD3xCETdCel1StKYtBoI25kMczkpHLdUa+Omn6jsOy8wJTN0DGLyQ2YUnPNpaJW3O5zsAXcK2AFv2IFrriYggvTTktPUxul90/WkJ7qbD3t5Cr4w9s4dEBu4zCSJ/LobRwxwxbgU8KM5IkleiFHJHjrNQd/U03klk0YvFQQfi9dKIN37iLhba7FO5f8MDaXurRdG6S7ncYB0UVSUvQ+SKN45o7ezqG6iP2H3xNP3ReyaZDy9KgfCaEYduKJN1wa6JqfZM6M4oepyqsSjOLgxvfqHZPTAQlNBxyXGksXXqaKoONOgEEAxSWwCtWmWvPAnLQSCv8sKUdC8sNG8ls1QeLwD3qTY4PoT2SbNLh7QHQ8xGrgnlpaJ41qHxgD8gRjBp2gLLqIrvnc9R0mpriVobDITmn0Bg/tWCbdgJ42Ae8sGkC4ZJ2DwjQRAGH4YD69LAJxV2YNRDZBg9sHeqvWJKIaWQaNXuURIoihwaP05fZBY3Ca5NnCeyOGMk3BccWxmbapt2r8sMoMVxNZ7byUlzspkGaGAEJZ2buirTeH1yNov8x6BC1WWh6kZZsOuR7BRHZtV7d+8EaCGXQgjcW2X0W2f4KCs3Qa6ySYkWdgF3OdB7ty6vBCD+MWWughdm90eKGHCciFHiayUB3cStCbgRgggI+6C7YDgSCBZOaGxsJwMYhIkGOSA+/ADxu3bFTTusiwHSwMRxupDLyRILIJ/MT1bSiSJOgbFIITQ8HuYNEtHfOmJ9FaYGlNi+xKR3ftaBJpaIuHlCKbvcFdO8bS1s4AvyTJLgm93oP32Y1oOe6aXlGliU4dN/fYlWmarskyXW7BRZPZKLp2ph3ZB45e7GFIM8RIhcIp6Ov4mElscFxB78d2NKOgOltBpXlqqYfuU29gn05kwTi4T8cyg9bfENy/ciAC3KTDYrXexuGvqeAa5dPiIA/mIyEQwa4voqMjs+0cGxypKm/+NJFFyeilHpFcQeEzz8iqZHBzztg30k7EtvwWYDQWljzJZi8gKJvkOmqTKIMsuSvCUJtEeW2lbVJsG/F36hGTI3+DjfypHzM+N/Kn+yVZkl9c+orBQpiOnBkyhIV3lpMhGp+NPO1qMsThHWyCqIWnQVULuU9kETW4HefRrbRU9yiwiLoF95Y6zdOA5yJLUgozw6DN2abJ0ZMkOam4aeKoDLizxj4MJm8ok2kClVlU2ZKr+uD1cIpEgNqSV05VtnG7ykOZp3JVP7L+GdxVYxUv88C9W2QBNLilxvI5wVrhIfVyS6AxHTUuPTeBMvtGf/RsppGhu3irM40ia5yX8mwnha3MkD2JlD1r5FMrDrRTSzQmWKueWnGgQ4dsTIjs1K5u9/C9NOlEHezi+1eJPTfl1pu310ozI7OAIoxKmieXchirl2ilUUJMl3KQ/4rvkI00kX3p6J0cIZb/42PtcoOiUQiATPYf8DVkbOikzfQSgp+lyVnFVY5DbuAuGh10e5BbZLM3QOFaSE3SSQcOCtUZKQ/PRJqfGfPDNC0BFlfVCB0K24bjTFgJFkHjK1KRFd/gThzvBb+pDn5PHLIDN+OETqwsvScPv6dXWGqiV8dtP3Z1mrOOaRsbDJRq+72VXHVrj0CLLAcH9+Q46/kdK3ScVm47+Glp6hArHNfUAJ3GFNNU1vCWrKm6Wyl7uDPHQztzIgvHwZ05IWbZPL6SGFlzDW7OiYVvvbHD31QT81RaMHhDKJsQmkCrtbvKwGIGzwl+mKLTFIvbNQ6NgLt0fCyJ0A2kpTyBB7fpeG0aDOICT98BVm1J6xR0snWCVqFEJyPmKRc1E52L2KfasFloou+rBR+ZnhR4aFLgI27NhNykQNjjWEBxGSwGIGH6dmZIEnYQ/qKSFAndDC3EF5ckDgRhk0inFAu2WkiNAkeCwO07XhkeljZQLQkcmHiucWrA2Q1pSQICBm1P9YrX0MaCw2wT5SOHKXJYcRPF4RtwF0/wOmaj0HrXBHizqM4lcwMCFIRxmseEmm4eTgZhQuSw2qsaAwdhwM08QUfrQ3hvx0EYcD9PUDG4Cg7DjysnX0pDT0hPWqAUw12cyDQnt8/Q+8hhlVsNbVcOgjkpAGaGBB4wGZWWNFm3kupwk4RfpEkiOL/y3RP7RpBNErarAtm03taTzvgJUOD6VWJ7iS24ML61tp4ZmQYUgLS6W1n90NZDJcYt0tVjpVt13eGunoDs6rEdR+LAXT1BRPEAfMRdcMcVCBFIpWXspQQWc8cQoi6zrycofpg2dRt7bBfZJo+mZYT2UDjbNYHCNZGdpJIU9rKFy4/dStEpermu03t+mKYVwuK6ytG7gK1Via5T/JLRa1Fsx8G75yrrg+Kp3jg9Ur3zPpjvjcPT+vftKxroop1uSO153wseSpF7ITNcyOiU8XS2UZ9+9fmd6BM9qYyXtINe9xLdf+xDCF6OG3Zq6fhQhWune88GSRttpdJgDVc8iQW37rkHRvxwTcLCrymSU2H7gTwd8i01/JJed/RMdOq4P8DuubZOMYPkCFiRXJW1bKiw8JWBD8VTMHTTXmfYDQ+YFE5Ny2Vgp6WmMllNsS0sXE1Ftprq3Qbxgy17sv82rmXPKp6XgVv2PDdruztC52WK52Xgjr1I1NZbOvhF6SZaW5qwdslok4JWFiMDn7KtXWTgk5CVg5IhTWinXc8Znod26NxB83Qd3KvnHJuLhU+xdLGaM4QjNmpHQgwmkVYpSG5JQqZVCo6fpWtbpYIjSU/MLyZnAQrLoea+TJncLEByD0B9bHEJLAYWQVr05mSTUNBnUTnisZqqzXbRHPQB71+2DWI+OjJ2FFvxdJqHV/hrKjd2dL5TFCiXOMTiCaYMOnLUaaZpSpNT0ruKuNYGclZxU8ZRHXAjnx+uoB0VNU0gOotGDqmds3sBgeHQEdxAhkx169hZwpGzSqub4cgMuIfPm5hPhIOow6z4dlr4PGWxyA4PypsXhs0krwjYWzBcGCBYGCBy7VJgZ0lb2y69zlSdK39YLrtTK3t4xZHU0Q1IWY2lh1ccSROQvVCmCprTePfeDOIPdo3cq8T2L1BwpU9j3XszMgwDxSaNdr1IHOzeU0ot0b1n+mPU4Z1cSgdk957hSB24e89LDgLgg+0mFgQtqqTJBA2DRd0YJkQnIKfPj6cnVXcCER4VmnXAkxmFVja7POZWPL9IUCMomuaHcT/jM9MZVukTVzku97BGsZYqWQ4SgVVJsHVkw3QNnCItDxFlKtKDt9uZ70cF81UfXxUMVo+r5SBIx/vuJLabzjBatsn1hMKy5jldXYE57ARWYKNpr6KFe8JmZreWDVcT1HSoTB5fNYvdS+ksU1OT6WkNmycj6/tZnh+C1dTbLtK6ruEpol0+RWwgah3eP2EWDHZqRIj0mudOVdytqWSHDR0v1TRv8WEIqXKBekNFc5TspY4qHDup9Ou5SA773p4Fd+Yvzt77s4t3Z2/esvfsreLd9AUvrzcfb3bP2z/RLv692NnOzYfL6zf7b3zeXF3tfvzidv1189flz9+O2r32l93v9u23NRdn5t3urN/utv3fWe+P/np3u/11/XZ7vd3F1Tfbm90pv2yur8lHC9jsMdkc3kMHnhvFJCvDXPdf3m63d4/fs3dDn37YXq13f+P/AQ==</diagram></mxfile>
用于实现哈希表的底层方法则是数组+链表或数组+红黑树(即平衡二叉B树,对平衡二叉树进行了优化,减少了调整平衡的开销)。



