Codeforces Round #796 (Div2) A~F题解

https://codeforces.com/contest/1688

打的稀碎，就不说结果了

A题

题意：
给定一个正整数$x$，找到最小的正整数$y$，使得$x AND y > 0$，$x XOR y > 0$。

思路：
要使得$x AND y > 0$， 显然$x和y$要至少有一个二进制位相同。
要使得$x XOR y > 0$， 显然$x和y$要至少有一个二进制位不同。
在此基础上找到最小的$y$即可。

void solve() {
	int x;
	cin >> x;
	int res = x & (-x);
	if(res == x) {
		for(int i = 0 ; i <= 30 ; i ++) {
			if(!(res & (1 << i))) {
				res |= (1 << i);
				break;
			}
		}		
	}
 
	cout << res << "\n";
}

B题

题意：
给定一个数组$a$，希望用最少的操作代价，使得$a$中所有元素均为奇数。可选操作为：
花费$1$的代价，将$a$中两个元素合并为它们的和。
花费$1$的代价，将一个偶数元素的值变为原来的一半。

思路：
这个sb题我都能wa两发，太菜了。
如果数组中有奇数的话，显然我直接将所有偶数合并，然后再加个奇数，就没有偶数了。
如果数组中全为偶数的话，我优先把除二次数最小就能变成奇数的偶数变成奇数，然后同上操作即可。

int a[N];
 
void solve() {
	int n;
	cin >> n;
	for(int i = 1 ; i <= n ; i ++) cin >> a[i];
	int s = 0, res = 0;
	int mind = 1e9;
	for(int i = 1 ; i <= n ; i ++){
		if((a[i] & 1) == 0) // 偶数的话
		{
			res ++;
			int cnt = 0;
			while(a[i] && (a[i] & 1) == 0) {
				cnt ++;
				a[i] >>= 1;
			}
			mind = min(mind, cnt);			
		}
		
	} 
 
	if(res == n) res = res - 1 + mind;
 
	cout << res << "\n";
}

C题

题意：
初始时有一个长度为$1$的由小写字母组成的字符串$s$。
它进行了$n$次操作，每次操作选择$s$的一个子串$t_1$和任意字符串$t_2$。
将$s$中的子串$t_1$替换成$t_2$。现在乱序给出这$n$个操作对应的两个字符串，以及$s$最终字符串$sfinal$。
求出初始的$s$。保证答案存在且唯一。

思路：
这个题真的是一点思路都没有，还是后面参考了别人的题解，才写的。

我只能说太女少了！

int cnt[30];
 
void solve() {
	memset(cnt, 0, sizeof cnt);
	int n;
	cin >> n;
	for(int i = 1 ; i <= n * 2 + 1 ; i ++) {
		string s;
		cin >> s;
		for(auto c : s) cnt[c - 'a'] ++;
	}
	for(int i = 0 ; i < 26 ; i ++)
		if(cnt[i] & 1){
			cout << (char)(i + 'a') << "\n";
			return;
		}
}

D题

题意：
给定一个数组$a$，可以选择任意下标为起点。然后按顺序执行以下操作$k$次：
当前坐标为$x$，可以改变下标为$x - 1, x, x + 1$的三者之一。
获取对应下标的值$a_x$，让$a_x = 0$。
整个数组值+1。

思路：
显然，当$k <= n$的时候，我们只需要找出长度为$k$的最大连续子段和
然后再$+0+1+...+(k - 1)$
当$k > n$的时候，那么首先整个数组的值肯定能取到，那么怎么走能获得最多的自增值呢？
很容易发现，我们呆在数组一端原地不走，等到$k == n - 1$的时候再开始向另一端走就可以得到最大值。

int a[N];
 
void solve() {
	int n, k;
	cin >> n >> k;
	for(int i = 1 ; i <= n ; i ++) cin >> a[i];
	int maxv = 0, s = 0; 
	int l = 1;
	for(int i = 1 ; i <= n ; i ++) {
		s += a[i];
		if(i - l + 1 > k) s -= a[l ++];
		maxv = max(maxv, s);
	}
	int res = maxv;
	if(k <= n) res += k * (k - 1) / 2;
	else {
		int p = k - 1;
		int c = p - n + 1;
		res += p * (p + 1) / 2 - c * (c + 1) / 2 + c;
	}
	cout << res << "\n"; 
}

E题

题意：
交互题。有一个无向图有$n$个点，和$m$条边，但是这个图为止（即不知道边怎么连的）。
现在可以进行至多$2m$次查询，然后求出这个无向图的最小权值完全生成森林。
即生成森林连通分量个数和无向图一样多，边权和最小。
每次可以询问一个长度为$m$的$01$串。$1$代表包含这条边。
系统回应由这些边组成的无向图的最大生成森林的值。

思路：
通过$m$次询问，每次只包含一条边，那么我们可以获得所有边的长度。
然后对边进行排序之后，按照kruskal的思想，我们每次加入一条边查询来判断一条边是否能加入后改变连通性，这样查询$m$次就能得到答案。

char s[N];
pii edge[N];
 
bool cmp(pii a, pii b){
	return a.x < b.x;
}
 
void solve() {
	int n, m;
	cin >> n >> m;
	for(int i = 0 ; i < m ; i ++) s[i] = '0';
	for(int i = 0 ; i < m ; i ++) {
		s[i] = '1';
		cout << "? " << s << endl;
		int len;
		cin >> len;
		edge[i] = {len, i};
		s[i] = '0';
	}
	sort(edge, edge + m, cmp);
	
	int minv = 0;
	for(int i = 0 ; i < m ; i ++) {
		int l = edge[i].x, now = edge[i].y;
		s[now] = '1';
		cout << "? " << s << endl;
		int len;
		cin >> len;
		if(minv + l == len) minv = len;
		else s[now] = '0';
	}
	cout << "! " << minv << endl;
}

F题

题意：
给定两个长度为$n$的数组$a$, $b$，以及$m$个区间$[l_i, r_i]$。
每次操作可以选择一个满足$\sum_{l_i}^{r_i}{a_i} = \sum_{l_i}^{r_i}{b_i}$的区间，让$[l_i, r_i]$这个区间$a$对应位置变成$b$对应位置的值。
问能够通过若干次操作将$a$变成$b$。能输出$YES$，否则输出$NO$。

思路：
令$c_i = a_i - b_i$，$s_i$为$c_i$的前缀和。
那么区间$[l_i, r_i]$操作合法等价于$s_{r_i} = s_{l_i - 1}$。
如果操作区间都不相交，那么我们直接进行合法操作，操作完判断即可。
对一个区间的操作，效果就是使得$c_{l_i} = c_{l_i + 1} = ... = c_{r_i} = 0$
也即$s_{l_i} = s_{l_i + 1} = ... = s_{r_i} = s_{l_i - 1}$
现在的问题是区间很可能是相交的，它们之间互相是有影响的，前面的操作可能会导致后面无法操作。

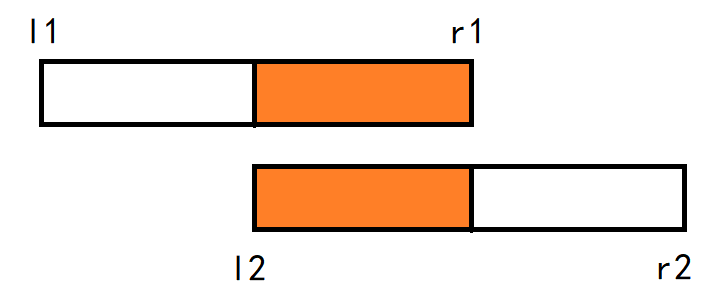
对于上面这两个区间。如果操作第一个区间，那么它会导致第二个区间$s_{l_2 - 1} = s_{l_1 - 1}$。
如果操作第二个区间，那么它会导致第一个区间$s_{r_1} = s_{l_2 - 1}$。
最终肯定是要所有的$s_i = 0$都成立。
我们如果选取的 $s_{r_i} = s_{l_i - 1} != 0$，那么事实上是没有什么意义的。
因为我们并没有使任何的$s_i = 0$，反而可能导致一些操作无法进行。
因此我们必然是选择 $s_{r_i} = s_{l_i - 1} = 0$的区间进行操作。
而对于这些区间，操作的顺序是没有关系的。

int a[N];
int b[N];
int c[N];
int s[N];

void solve() {
	int n, m;
	cin >> n >> m;
	for(int i = 1 ; i <= n ; i ++) cin >> a[i];
	set<int> st;
	// 两个数组一样，等价于差数组 c 的前缀和数组 s 全为 0  
	for(int i = 1 ; i <= n ; i ++) {
		cin >> b[i];
		c[i] = a[i] - b[i];
		s[i] = s[i - 1] + c[i];
		if(s[i]) st.insert(i);  // 如果当前点还未置零 放入set中 
	}
	
	queue<pii> que;		// 用于保存所有将执行操作的区间 
	vector<vector<pii>> v(n + 1);
	for(int i = 1 ; i <= m ; i ++) {
		int l, r;
		cin >> l >> r;
		if(!s[l - 1] && !s[r]) que.push({l, r});
		else {
			v[l - 1].push_back({l, r});
			v[r].push_back({l, r});
		}
	}
	
	while(!que.empty()) {
		auto u = que.front();
		que.pop();
		auto iter = st.lower_bound(u.x);	// 操作区间的起点 
		
		while(iter != st.end() && *iter <= u.y) {
			s[*iter] = 0;
			for(auto ints : v[*iter]) {		// 查看一下那些线段，有一端在当前操作区间的 ，置零后是否可以操作了 
				if(!s[ints.x - 1] && !s[ints.y]) {	// 可以操作了就放进队列里 
					que.push(ints);
				}
			}
			st.erase(iter ++);	// 删除当前点，该点已置零 
		}
		
	}
	
	if(st.empty()) {	// 所有点已经置零 
		cout << "YES\n";
	} else {
		cout << "NO\n";
	}
}