算法刷题：链表题（8.4，持续更）

迭代过程：
- 第一次迭代：
- 遍历（循环迭代、递归迭代）的退出条件、while 循环体最后，别忘了 p = p.next
- 迭代的区间（非遍历，只访问中间的一部分）：
- 最后一次迭代：
定义和初始化时
- 链表太短时（空指针异常）：head ?= null / head.next ?= null
分段：
- 逻辑分段：一段函数体的代码实现的功能，可能是几段逻辑按顺序排列，每段逻辑都可以单独作为起点，不要把逻辑弄混
- 定义和初始化按段定义：详情见 反转链表 II 的优化代码部分
具体题型：
- 比如跟随指针，一次迭代代码段（for/while循环），先前进、先跟随还是先关键代码，可能会影响迭代退出条件、简化一些边界情况
- 如果需要操作.next或者.next.next，必须先操作.next.next
- 哨兵节点 / 虚拟头节点：
  哨兵节点 dummyHeadNode，可以接收一列新链表或者存储原链表起点，简化一些边界情况的处理
- 并不知道一个链表的长度多少、也不知道多个链表的长度是否相等

下标排序和反转链表

下标排序：反序 -> 反转链表，正序

链表相交、成环

链表相交 -> 长短链对齐处理
成环处理 -> 相对速度绕环追赶
处理之后可能链表产生相交点 或者环
相交、环

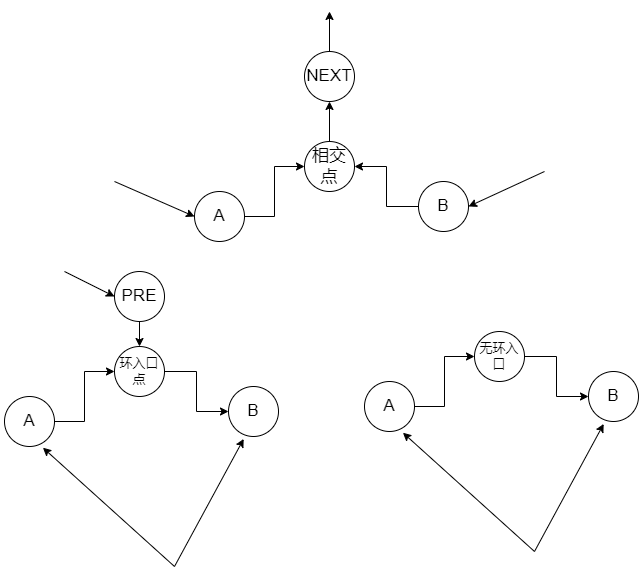
画图分析

穿针引线图

按一定规则排序下标的时候，可能需要画穿针引线图：
如果状态转换的结果是下标按规则重排序，那么就需要画穿针引线图

奇偶节点数链表 - 边界处理

奇数和偶数的节点数的链表，可能需要边界处理

1 多指针迭代

同时需要操作多个链表时，可以使用多个指针，分别记录各个链表的迭代位置，可以避免一些回溯

两数相加

未优化的代码（2ms）

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(), p = dummy;
        ListNode p1 = l1, p2 = l2;
        int val = 0;
        // 以 p、p1、p2 为起点迭代
        while(p1 != null && p2 != null){
            p.next = new ListNode();
            p = p.next;

            val += p1.val + p2.val;
            if(val > 9){
                p.val = val % 10;
                val = 1;
            } else {
                p.val = val;
                val = 0;
            }
            
            p1 = p1.next;
            p2 = p2.next;
        }
        ListNode p0 = p1 != null? p1 : p2;
        p.next = p0;
        if(val == 0 || p0 == null){
            if(val == 1) p.next = new ListNode(1);
            return dummy.next;
        } // val == 1， 开始以 p0 为起点迭代
        while(p0.next != null){
            if(p0.val != 9){
                p0.val ++;
                return dummy.next;
            }
            p0.val = 0; // 进 1 位
            p0 = p0.next; // 下一位
        }
        // 最后一位-单独处理（最后一位的进位需要new一个节点）
        if(p0.val == 9){
            if(val == 1){
                p0.val = 0; // 进 1 位
                p0.next = new ListNode(1);
            }
        } else {
            if(val == 1) p0.val++;
        }
        return dummy.next;
    }
}

优化后代码（1ms击败100%）

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode(), p = dummy;
        ListNode p1 = l1, p2 = l2;
        int val = 0;
        // 以 p、p1、p2 为起点迭代
        while(p1 != null || p2 != null){
            // 前置迭代
            p.next = new ListNode();
            p = p.next;
            // 取出 值（待处理内容）再 前置迭代
            int p1v = (p1 != null)? p1.val: 0;
            int p2v = (p2 != null)? p2.val: 0;
            if(p1 != null)p1 = p1.next;
            if(p2 != null)p2 = p2.next;

            // 处理点
            val += p1v + p2v;
            if(val > 9){
                p.val = val % 10;
                val = 1;
            } else {
                p.val = val;
                val = 0;
            }
        }
        // 最后一位-单独处理（最后一位的进位需要new一个节点）
        if(val == 1) p.next = new ListNode(1);
        return dummy.next;
    }
}

合并 2 个有序链表

^{多指针迭代}解法（\(O(N)\))

目标链表虚拟头节点dummy + 同时迭代 2 个源链表和 1 个目标链表

操作模型：

for -> cur = min(list1 OR list2)

关键代码：

// 定义：虚拟头节点 dummy + 目标链表迭代器 p
ListNode dummy = new ListNode(0);
ListNode p = dummy;
// 核心逻辑：合并到目标链表
p.next = list;
list = list.next;
p = p.next;
// 返回值
return dummy.next;

实现代码：

细节优化前：

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode dummy = new ListNode(0);
        ListNode p = dummy;
        while(list1 != null || list2 != null){
            if(list1 == null){
                p.next = list2;
                break;
            } else if(list2 == null) {
                p.next = list1;
                break;
            }
            if(list1.val < list2.val){
                p.next = list1;
                list1 = list1.next;
            } else {
                p.next = list2;
                list2 = list2.next;
            }
            p = p.next;
        }
        return dummy.next;
    }
}

细节优化后：

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if(list1 == null) return list2;
        if(list2 == null) return list1;

        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;
        ListNode p1 = list1;
        ListNode p2 = list2;

        while(p1 != null && p2 != null) {
            if(p1.val < p2.val){
                cur.next = p1;
                p1 = p1.next;
            } else {
                cur.next = p2;
                p2 = p2.next;
            }
            cur = cur.next;
        }
        cur.next = p1 != null ? p1 : p2;
        return dummy.next;
    }
}

合并 k 个有序链表

^{K个中minNode}解法 (\(O(K * N)\))

每次迭代，比较 K 个链表头，求最小值 minNode，加入返回链表
直到迭代完所有链表
时间复杂度 \(O(K * N)\)
运行时间：210ms
操作模型：

for -> (cur = min(lists.forEach -> node))

优化细节前代码：

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if(lists == null) return null;
        if(lists.length == 0) return null;

        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;

        ListNode min;
        int minPos;
        boolean keep = true;

        while(keep){
            keep = false;
            minPos = 0;
            min = lists[0];
            
            for(int p = 0; p < lists.length; p++) {
                if(lists[p] == null) continue;

                if(keep != true) keep = true;

                if(min == null || (lists[p]).val < min.val) {
                    min = lists[p];
                    minPos = p;
                }
            }

            if(keep != true) break;

            cur.next = min;
            lists[minPos] = min.next;
            cur = cur.next;
        }

        return dummy.next;
    }
}

优化细节后：

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode dummy = new ListNode(0);
        ListNode cur = dummy;

        ListNode minNd;
        int minPos;

        while(true){
            minPos = -1;
            minNd = null;
            
            for(int i = 0; i < lists.length; i++) {
                if(lists[i] == null) continue;

                if(minNd == null || lists[i].val < minNd.val) {
                    minNd = lists[i];
                    minPos = i;
                }
            }
            if(minPos == -1) break;

            cur.next = minNd;
            lists[minPos] = lists[minPos].next;
            cur = cur.next;
        }

        return dummy.next;
    }
}

排序队列取minNode队头

^{手动实现的排序队列}解法 (\(O(K * N)\))

运行时间：216ms

class Solution {
    static class SortedQueue {
        private static final LinkedList<ListNode> list = 
			new LinkedList<>();

        ListNode popHead() {
            return list.removeFirst();
        }
        void sortedPut(ListNode insert){
            if (insert == null) return;
            int index = 0;
            for (ListNode node : list) {
                if (node.val >= insert.val){
                    list.add(index, insert);
                    return;
                }
                index++;
            }
            if (index != 0){
                list.addLast(insert);
            } else {
                list.addFirst(insert);
            }
            return;
        }
        @Override
        public String toString() {
            StringBuilder builder = new StringBuilder();
            for (ListNode node : list){
                builder.append(node.val).append(" ");
            }
            return builder.toString();
        }
    }
}

未加嵌套的单次逻辑：

public ListNode mergeKLists(ListNode[] lists) {
     ListNode dummy = new ListNode(0);
     ListNode p = dummy;

     SortedQueue queue = new SortedQueue();

     p.next = queue.popHead();
     if(p.next.next != null){
        queue.sortedPut(p.next.next);
     }
     p = p.next;
 }

加入嵌套、嵌套退出的条件：

while(queue.list.size() != 0){ ...... }

完整代码：

class Solution {
    static class SortedQueue {
        static final LinkedList<ListNode> list = new LinkedList<>();

        ListNode popHead() {
            return list.removeFirst();
        }
        void sortedPut(ListNode insert){
            if (insert == null) return;
            int index = 0;
            for (ListNode node : list) {
                if (node.val >= insert.val){
                    list.add(index, insert);
                    return;
                }
                index++;
            }
            if (index != 0){
                list.addLast(insert);
            } else {
                list.addFirst(insert);
            }
            return;
        }
    }

    public ListNode mergeKLists(ListNode[] lists) {
        ListNode dummy = new ListNode(0);
        ListNode p = dummy;

        SortedQueue queue = new SortedQueue();
        for(ListNode node : lists){
            queue.sortedPut(node);
        }

        while(queue.list.size() != 0){
            p.next = queue.popHead();
            if(p.next.next != null){
                queue.sortedPut(p.next.next);
            }
            p = p.next;
        }
        return dummy.next;
    }
}

^{优先级队列}解法 ( \(O(N log(K))\))

本质是小根堆，小根堆的根节点就是最小值，相比于我实现的队列，它的插入效率更高
运行时间：4ms

class Solution {
   public ListNode mergeKLists(ListNode[] lists) {
        if (lists == null || lists.length == 0) return null;
        PriorityQueue<ListNode> queue = new PriorityQueue<>(lists.length, new Comparator<ListNode>() {
            @Override
            public int compare(ListNode o1, ListNode o2) {
                if (o1.val < o2.val) return -1;
                else if (o1.val == o2.val) return 0;
                else return 1;
            }
        });
        ListNode dummy = new ListNode(0);
        ListNode p = dummy;
        for (ListNode node : lists) {
            if (node != null) queue.add(node);
        }
        while (!queue.isEmpty()) {
            p.next = queue.poll();
            p = p.next;
            if (p.next != null) queue.add(p.next);
        }
        return dummy.next;
    }
}

^分治解法：两个一组逐渐合并 (\(O(N log(K))\))

特点是每次合并完就会少一半的（\(O(log K)\)）
运行时间：1ms

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if(lists == null || lists.length == 0){
            return null;
        }
        return spilt(lists , 0 , lists.length - 1);
    }
    public ListNode spilt(ListNode[] lists , int i , int j){
        if(i == j){
            return lists[i];
        }
        int m = (i + j) >>> 1;
        ListNode left = spilt(lists , i , m);
        ListNode right = spilt(lists , m+1 , j);
        return mergeTwoLists(left, right);
    }
    public ListNode mergeTwoLists(ListNode p1, ListNode p2) {
        ListNode s = new ListNode(-1, null);
        ListNode p = s;
        while (p1 != null && p2 != null) {
            if (p1.val < p2.val) {
                p.next = p1;
                p1 = p1.next;
            } else {
                p.next = p2;
                p2 = p2.next;
            }
            p = p.next;
        }
        p.next = p1 != null ? p1 : p2;
        return s.next;
    }
}

分隔链表

^{多指针迭代}解法（\(O(N)\))

class Solution {
    public ListNode partition(ListNode head, int x) {
        ListNode p = head;
        ListNode lowDummy = new ListNode(0);
        ListNode highDummy = new ListNode(0);
        ListNode low = lowDummy;
        ListNode high = highDummy;

        while(p != null){
            if(p.val < x){
                low.next = p;
                low = low.next;
            } else {
                high.next = p;
                high = high.next;
            }
            ListNode q = p.next;
            p.next = null;
            p = q;
        }
        low.next = highDummy.next;
        return lowDummy.next;
    }
}

2 快慢指针

理论解析：快慢指针的切入点

快慢指针可以以不同的速度迭代：

速度的倍数关系：速度 2 是速度 1 的 2 倍速
相对速度：速度 2 和速度 1 的 相对速度是 1
- 指针变量定义：slow、fast
跟随问题：快指针先向前，但是慢指针随后就能跟上
- 指针变量定义：master、follow 或 pre、cur、nxt
长短链迭代完成速度问题：

速度倍数题：

链表的中间节点 ( \(O(N)\) )

思路：

如何找到中间节点：求长度、2 倍速的快慢指针
关键代码：

// 定义快慢指针
ListNode fast = head;
ListNode slow = head;
// 核心：快慢迭代
slow = slow.next;
fast = fast.next.next;
// 返回值
return slow;

迭代退出条件：while fast && fast.next
完整代码：

class Solution {
    public ListNode middleNode(ListNode head) {
        if(head == null) return null;
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

删除链表的中间节点 ( \(O(N)\) )

思路：

找到中间节点
- 如何找到中间节点：求长度、2 倍速的快慢指针
删除中间节点
- 需要中间节点的前一个节点
- 如何让慢指针慢一步？

slow = head;
fast = head.next;

分析结束，开始梳理
关键代码：

// 定义快慢指针
ListNode fast = head.next;
ListNode slow = head;
// 核心：快慢迭代
slow = slow.next;
fast = fast.next.next;
// 核心：删除中点（快指针遍历结束）
ListNode temp = slow.next;
slow.next = temp.next;
temp.next = null;

迭代退出条件：while fast.next && fast.next.next

完整代码：

class Solution {
    public ListNode deleteMiddle(ListNode head) {
        if (head == null || head.next == null) {
            return null;
        }
        ListNode slow = head;
        ListNode fast = head.next;

        while(fast.next != null && fast.next.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        ListNode temp = slow.next;
        slow.next = slow.next.next;

        temp.next = null; // 帮助垃圾回收
        return head;
    }
}

相对速度题：

环形链表 ( \(O(N)\) )

思路：

什么是链表成环？
- 首尾相接
- 尾接到中间的某个节点
是否成环：
- 如果成环：两指针进入环后，快慢指针相对速度1，意味着快慢指针会不断缩短距离，直到它们相遇
- 如果不成环：快指针迭代到 null

关键代码：

// 定义快慢指针
ListNode slow = head;
ListNode fast = head;
// 核心：快慢迭代
slow = slow.next;
fast = fast.next.next;
// 核心：处理成环情况
if(slow == fast) return true;
// 核心：处理不成环情况
if(fast.next == null || fast.next.next == null){
	return false;
}
// 迭代退出条件
while(slow != fast){
	// --- 迭代逻辑 ---
}

完整代码：

public class Solution {
    public boolean hasCycle(ListNode head) {
        if(head == null){
            return false;
        }
        ListNode slow = head;
        ListNode fast = head;
        do {
            if(fast == null 
                || fast.next == null){
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
        } while(slow != fast);
        return true;
    }
}

环形链表的环形入口（\(O(N)\)）

^数学建模分析

切入点：

各部分长度和迭代次数的关系

首先进入环之前，是有长度的：

环前长度：\(a\)
环长度：\(m\)

环长度还可以分解：

环形入口到相遇点的长度：\(b\)
相遇点到环形入口的长度：\(c\)

时间线：

在慢指针刚进入环入口时，也就是说，慢指针走了环前长度的距离：
- 快慢指针迭代次数：\(a\)
- 慢指针长度：\(a\)
- 快指针长度：\(2a\)
- 此时快指针离环入口：\((b + c) % a\) 的距离
- \(b = (b + c) % a\)
- 额外圈数：\(k = (b + c) / a\)
从慢指针 迭代到环入口 到其 迭代到快慢指针相遇
- 快慢指针迭代次数：\(a + b\)
- 慢指针路程长度：\(a + b\)
- 快指针路程长度：\(2a + 2b = a + b + k * (b + c)\)

公式化简：

\(2a + 2b = a + b + b + c + (k - 1) * (b + c)\)
\(a - c = (k - 1) * (b + c)\)
\(a = c + (k - 1) * (b + c)\)

分析公式：

(a - c) 是环长的倍数
那么 (a - c) 是什么？
- c 是环长 - 相遇点，环长不知道，c 是未知量
- 那么 a - c 可不可以当成整体来看？
- 从什么时间点看？
a 是环前长度，此时我构造一个辅助节点开始从头节点跟 slow 同时迭代，slow 走了c 长度这个未知量之后，slow 回到环形入口点，而此时辅助节点的剩余距离是环形长度的整数倍，也就是说：
若在快慢指针相遇时，辅助节点从头节点迭代、slow继续迭代，那么 slow 和辅助节点最终可以在入口处相遇

代码实现

关键代码：

// 定义快慢指针 \ 数学公式需要的指针
ListNode slow = head;
ListNode fast = head;
ListNode help = head;

// 核心：快慢指针相遇
do {
    if(fast == null 
        || fast.next == null){
        /* 不成环 */
    }
    slow = slow.next;
    fast = fast.next.next;
} while(slow != fast);
/* 成环，并且快慢指针相遇 */

// 核心：辅助指针开始移动、slow继续移动，最终相遇
while(slow != help){
	slow = slow.next;
	help = help.next;
}
// 返回值
return head;

完整代码：

ublic class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
		// ListNode help = head;
		// 辅助指针 help 的作用，可以由 fast 替代

        do {
            if(fast == null 
                || fast.next == null){
                return null;
            }
            slow = slow.next;
            fast = fast.next.next;
        } while(slow != fast);

        fast = head;
        while(slow != fast){
        	slow = slow.next;
        	fast = fast.next;
        }
        return slow;
    }
}

跟随(pcn) + 穿针引线

反转链表（\(O(N)\)）

这个可以用跟随模型来解决：

^快慢指针解法-画图分析、代码实现

这里用图来分析（反转一个4节点链表）：
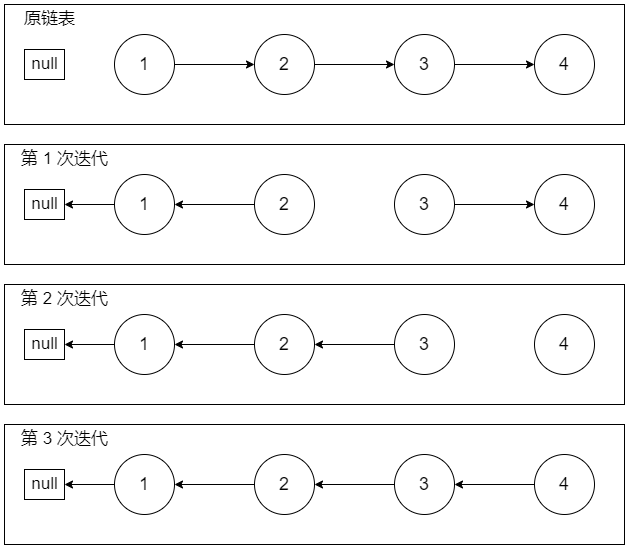
反转链表示例

class Solution {
    public ListNode reverseList(ListNode head) {
        // 边界：链表小于两个节点
        if(head == null || head.next == null){
            return head;
        }

        // 定义多指针
        ListNode follow2 = head;
        ListNode follow1 = head.next;
        ListNode master = head.next.next;

        // 开始迭代
        // 边界：第一次迭代
        follow1.next = follow2;
        follow2.next = null;
        // 非边界迭代
        while(master != null) {
            // 迭代
            follow2 = follow1; // follow2 跟上 follow1
            follow1 = master; // follow1 跟上 master
            master = master.next; // master 向前走一步
            // 操作
            follow1.next = follow2;
        }
        follow1.next = follow2;
        return follow1;
    }
}

^递归解法（\(O(N)\)）

递归解法在链表比较长时，可能会栈溢出（StackOverflow）：
(额外空间复杂度：O（n），因为调用了N层栈空间)

首先写一个递归遍历链表的函数：

public ListNode traverse(ListNode cur){
    // 递归退出条件
    if(cur == null) return null;
	
    // 递归获得下一个
    ListNode nxt = traverse(cur.next);
	
	  /* 
	   * 遍历时额外的操作 / 反转链表的核心操作单元
	   */

    // 向上一个返回当前节点
    // 当前节点相对于上一个，就是下一个
    return cur;
}

定义遍历时的递归链表中每一节点的操作

// 核心逻辑：一次反转相邻节点操作
if(nxt != null){
	nxt.next = cur;
	cur.next = null;
}

递归遍历的承载函数：

public ListNode reverseList(ListNode head) {
    if(head == null) return null;

	// 提前获取头节点
    ListNode tail = head;

    while(tail.next != null){
        tail = tail.next;
    }
	 // 遍历 + 反转
    traverse(head);

    return tail;
}

完整代码：

class Solution {
    public ListNode reverseList(ListNode head) {
        if(head == null) return null;

        ListNode tail = head;

        while(tail.next != null){
            tail = tail.next;
        }
        traverse(head);

        return tail;
    }
    public ListNode traverse(ListNode cur){
        if(cur == null) return null;

        ListNode nxt = traverse(cur.next);

        if(nxt != null){
            nxt.next = cur;
            cur.next = null;
        }
        return cur;
    }
}

^新建链表解法(其实类似跟随指针)

额外空间复杂度：\(O(N)\)

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode follow = null;
        ListNode master = null;
        
        for(ListNode p = head; p != null; p = p.next){
            master = new ListNode(p.val);
            master.next = follow;
			
            follow = master; // 跟上 master
        }
        return master;
    }
}

反转链表的中间某段 / 反转链表 II

^快慢指针解法（\(O(N)\)）

思路：

首先先找到第 \(left\) 位置的节点
之后迭代 \((right - left)\) 次，进行反转
之后将反转的中间部分和链表的其余部分进行对接

关键代码：

// 定义 跟随指针
ListNode pre = head;
ListNode cur = null;
ListNode nxt = null;
// 核心逻辑：找到 left 位置的节点
for(int i = 0; i < left - 1; i++){
	pre = pre.next;
}
ListNode start = pre; // 记录端点
pre = pre.next;
cur = pre.next;
nxt = cur.next;
// 核心逻辑：进行中间段的链表反转
int len = right - left;
for(int i = 0; i < len; i++){
	// 开始反转
	cur.next = pre;
	pre.next = null;
	// 开始跟随
	pre = cur;
	cur = nxt;
	nxt = nxt.next;
}
// 核心逻辑：反转后 和 链表中间段端点进行对接
start.next.next = nxt;
start.next = cur;

return head;

加入细节后的完整代码：

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right){
        if(left == right) return head; // 优化
        if(head == null) return null; // 边界

        ListNode pre = head;
        ListNode cur = null;
        ListNode nxt = null;
        
        ListNode start = null;

        for(int i = 0; i < left - 2; i++){
            pre = pre.next;
        }

        if(pre == null){
            return head;
        }

        start = pre;
        if(left > 1) { // 边界
            pre = pre != null ? pre.next : null;
        }
        cur = pre != null ? pre.next : null;
        nxt = pre != null && pre.next != null ? pre.next.next : null;
        
        if(cur == null) { 
            return head;
        }

        int len = right - left;
        pre.next = null;
        for(int i = 0; i < len && cur != null; i++){
            cur.next = pre;
            pre = cur;
            cur = nxt;
            
            if(nxt != null) {
                nxt = nxt.next;
                continue;
            } break;
        }
        if(left != 1){ // 边界，防止成环
            // 1 2 3 4 5, l: 2，r: 4
            start.next.next = cur; // 2的后继是5
            start.next = pre; // 4的前驱是1
            // ~!!注意，必须先修改.next.next之后，才能修改.next
        } else { // 换头节点
            head = pre;
            start.next = cur;
        }
        return head;
    }
}

优化代码

优化思路：

逻辑分段
定义与初始化变量，按逻辑分段

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        if(left == right) return head; // 优化
		
        /* 第 1 段逻辑：迭代到 left 边界
		      **/  // 定义和初始化变量
        ListNode dummy = new ListNode(0, head);
        ListNode p = dummy; // p就是start

        for (int i = 0; i < left - 1; i++){
            p = p.next;
        }
        /* 第 2 段逻辑：反转
		      **/  // 定义和初始化变量
        ListNode pre = null;
        ListNode cur = p.next;
        ListNode nxt = null;
        for (int i = 0; i < right - left + 1; i++) {
            nxt = cur.next; // 前进
			 
            cur.next = pre; // 反转
			
            pre = cur; // 跟随前进
            cur = nxt;
        }

        p.next.next = cur;
        p.next = pre;
        return dummy.next;
    }
}

K 个一组反转链表

^{求长度分别反转}解法（\(O(K * N)\)）

直接0ms，超过100%

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
		// 求长度
        int len = 0;
        for(ListNode p = head ; p != null; ++len, p = p.next);

		// 开始反转
        int n = len / k;
		
        ListNode dummy = new ListNode(0, head);
        ListNode p = dummy;
        for(int i = 0; i < n; i++){
            ListNode pre = null;
            ListNode cur = p.next; // 这里
            ListNode nxt = cur;
            for(int j = 0; j < k; j++){
                nxt = cur.next; // 前进
				
                cur.next = pre; // 反转
				
                pre = cur; // 跟随
                cur = nxt;
            }
            p.next.next = nxt;
			// 这里需要修改 p.next，还需要修改之前的 p.next
			// 于是引入了临时变量 temp 存储修改前的 p.next
            ListNode temp = p.next;
            p.next = pre;
            p = temp;
        }
        return dummy.next;
    }
}

重排链表

题目描述的分析：

原链表：
\(L0 → L1 → … → Ln - 1 → Ln\)
目标链表：
\(L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …\)

思路：
题目描述了一种状态转换，但是什么地方状态转换？

链表的下标进行了反序，这不就是反转单链表？

本质是链表下标序反序，马上联想到 '反转链表'
代码：

class Solution {
    public void reorderList(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        
        ListNode pre = null;
        ListNode cur = slow;
        ListNode nxt = cur;
        while(cur != null){
            nxt = nxt.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }

        fast = head;
        // while(pre != null && pre.next != null){
        while(pre.next != null){
            nxt = fast.next;
            cur = pre.next;

            fast.next = pre;
            pre.next = nxt;

            pre = cur;
            fast = nxt;
        }
    }
}

回文链表

思路：链表中间节点+反转链表（相交链表）

其实图解之后，和回文链表的图解是一样的

^{反转后半部分}解法（\(O(N)\)）

本质就是：fs速度倍数 + pcn跟随
运行时间：2ms，击败 100%
代码：

class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
		// 此时相当于在 slow 节点上有 2 个相交链表
		// 1，2，3
        if(fast != null){
            slow = slow.next;
        }

        ListNode pre = null;
        ListNode cur = slow;
        ListNode nxt = cur;
        while(cur != null){
            nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }

        ListNode phead = head;
        while(pre != null){
            if(pre.val != phead.val){
                return false;
            }
            pre = pre.next;
            phead = phead.next;
        }
        return true;
    }
}

^{反转前半部分}解法（\(O(N)\)，更优）

运行时间：3ms，击败 97%

class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        ListNode pre = null;
        ListNode cur = head;
        while(fast != null && fast.next !=null){
            slow = slow.next;
            fast = fast.next.next;

            cur.next = pre;
            pre = cur;
            cur = slow;
        }

        if(fast != null){
            slow = slow.next;
        }

        while(pre != null){
            if(pre.val != slow.val){
                return false;
            }
            slow = slow.next;
            pre = pre.next;
        }
        return true;
    }
}

长短链迭代完成速度题

相交链表

对齐长度解法

其实找到交点很简单，因为公共部分是对齐的，所以问题就是：两链表长度可能不对齐，要想办法去除长度差值进行对齐

^{求长度·对齐}解法（\(O(N)\)）

思路：

可以求长度
之后再根据长度的差值进行对齐

问题：

求长度意味着除了迭代还要给长度计数器赋值，多了计数器赋值计数的时间

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode pA = headA;
        ListNode pB = headB;

        // 计算长度
        int lenA = 0;
        int lenB = 0;
        for(lenA = 0; pA != null; pA = pA.next, ++lenA);
        for(lenB = 0; pB != null; pB = pB.next, ++lenB);
        pA = headA;
        pB = headB;

        // 长链表的移动长度差值距差
        if(lenA < lenB){
            for(int i = 0; i < lenB - lenA; i++){
                pB = pB.next;
            }
        } else {
            for(int i = 0; i < lenA - lenB; i++){
                pA = pA.next;
            }
        }

        // 开始比较是否重复
        while(pA != pB){
            pA = pA.next;
            pB = pB.next;
        }
        return pA;
    }
}

^{迭代完成快慢对齐}解法（\(O(N)\)）

拼接对齐法不需要计算长度，而是根据：

长短链表迭代过程中长度差异导致的结果：
短的链表必定先迭代完，之后对长链表的剩余节点迭代就能表示出长短链表的长度差值

启示：

短链和长链同时迭代，短链迭代完成速度快，长链迭代完成速度慢

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode pA1 = headA;
        ListNode pB1 = headB;
        while(pA1 != null && pB1 != null){
            pA1 = pA1.next;
            pB1 = pB1.next;
        }

        ListNode pA2 = headA;
        ListNode pB2 = headB;
        while(pA1 != null){
            pA1 = pA1.next;
            pA2 = pA2.next;
        }
        while(pB1 != null){
            pB1 = pB1.next;
            pB2 = pB2.next;
        }

        while(pA2 != pB2){
            pA2 = pA2.next;
            pB2 = pB2.next;
        }
        return pA2;
    }
}

^{拼接成环型链表}解法（\(O(N)\)）

构造成环形链表，之后按照环形链表的入口点思路、快慢指针（相对速度）+数学公式推导进行解决：（这里相交点就是入口点）
图解：
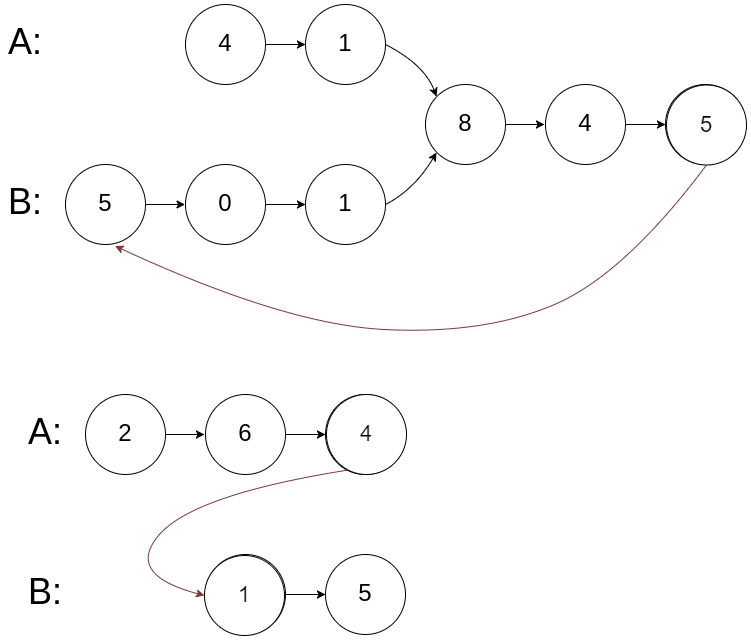
成环示意图

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
		// 成环
        ListNode pA = headA;
        while(pA.next != null){
            pA = pA.next;
        }
        ListNode endA = pA;
        pA.next = headB;

		// 按照成环的入口点思路进行解决
        ListNode head = headA;
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast){
                fast = head;
                while(slow != fast){
                    slow = slow.next;
                    fast = fast.next;
                }
				// 断开之前的环接点
                endA.next = null;
                return slow;
            }
        }
		// 断开之前的环接点
        endA.next = null;
        return null;
    }
}

3 排序

基础排序（\(O(N^2)\)，超时）

冒泡排序

单次迭代（单次冒泡）的代码：

如果当前节点cur比下一节点nxt大，那么交换彼此的位置
交换需要穿针引线，根据穿针引线图

ListNode dummy = new ListNode(0, head);
 // ListNode end = null;

ListNode pre = dummy;
ListNode cur = pre.next;
ListNode nxt = cur.next;
// 如果当前节点cur比下一节点nxt大，那么交换彼此的位置
// 交换需要穿针引线，根据穿针引线图
// 写出下面的代码
while(nxt != null){ // nxt != end
   if(cur.val > nxt.val){
      pre.next = nxt;
      cur.next = nxt.next;
      nxt.next = cur;
    }
    pre = pre.next;
    cur = pre.next;
    nxt = cur.next;
}
System.out.println(cur.val); // 链表最大值，用于测试是否冒泡成功
return dummy.next;

嵌套/迭代/排序的最后一步操作：end 指向第一个节点（dummy.next）

while(end != dummy.next){ 
	………
	while(nxt != end){
		………

加入嵌套的完整代码：

class Solution {
    public ListNode sortList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        // bubbleSort
        ListNode dummy = new ListNode(0, head);
        ListNode end = null;
        while(end != dummy.next){
            ListNode pre = dummy;
            ListNode cur = pre.next;
            ListNode nxt = cur.next;
            while(nxt != end){
                if(cur.val > nxt.val){
                    pre.next = nxt;
                    cur.next = nxt.next;
                    nxt.next = cur;
                }
                pre = pre.next;
                cur = pre.next;
                nxt = cur.next;
            }
            end = cur;
        }
        return dummy.next;
    }
}

选择排序

略

插入排序

略

归并排序（\(O(NlogN)\)）

运行时间：10~15ms，不如计数排序
通过递，将整个链表分解成 1~2 个节点一组；
通过归，将分解的链表排序的结果返回

自顶向下归并

直接写出来

class Solution {
    public ListNode sortList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode slow = head;
        ListNode fast = head;
        // int count = 0;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        fast = slow.next;
        slow.next = null;

        ListNode p1 = head;
        if(head.next.next == null){
            if(head.val > head.next.val){
                head.next.next = head;
                p1 = head.next;
                head.next = null;
            }
        } else {
            p1 = sortList(head);
        }
        ListNode p2 = sortList(fast);

		// 归并两个有序链表
        ListNode dummy = new ListNode(), p = dummy;
        while(p1 != null && p2 != null){
            // System.out.println(p1.val + " " + p2.val);
            if(p1.val < p2.val){
                p.next = p1;
                p1 = p1.next;
            } else {
                p.next = p2;
                p2 = p2.next;
            }
            p = p.next;
        }
        if(p1 != null){
            p.next = p1;
        } else p.next = p2;
        return dummy.next;
    }
}

优化代码：

处理中点分隔的边界点

ListNode prev = null; ////
while (fast != null && fast.next != null) {
    prev = slow; ////
    slow = slow.next;
    fast = fast.next.next;
}
pre.next = null; /// 
// fast = slow.next;
// slow.next = null;
// ListNode p1 = head;
// if(head.next.next == null){
//    if(head.val > head.next.val){
//        head.next.next = head;
//        p1 = head.next;
//        head.next = null;
//    }
//} else {
//    p1 = sortList(head);
//}
ListNode p1 = sortList(head);
ListNode p2 = sortList(slow);

抽离 merge 方法：
- merge 方法就是：合并两个有序链表 的代码

class Solution {
    public ListNode sortList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        ListNode prev = null;
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            prev = slow;
            slow = slow.next;
            fast = fast.next.next;
        }
        prev.next = null;
        return merge(sortList(head), sortList(slow));
    }
    static public ListNode merge(ListNode head1, ListNode head2){
	    ListNode dummy = new ListNode(), p = dummy;
	    ListNode p1 = head1, p2 = head2;
	    while(p1 != null && p2 != null){
		    if(p1.val < p2.val){
			    p.next = p1;
			    p1 = p1.next; // while迭代的最后一步，p = p.next
		    } else {
		    	p.next = p2;
		    	p2 = p2.next; // ---
		    }
		    p = p.next; // while迭代的最后一步，p = p.next
	    }
	    if(p1 != null){
	    	p.next = p1;
	    } else p.next = p2;
	    return dummy.next;
    }
}

自底向上归并

归并排序的本质是：对局部的整体排序，再合并两个有序链表-插入归并成整体

画图分析和流程分析

图示：
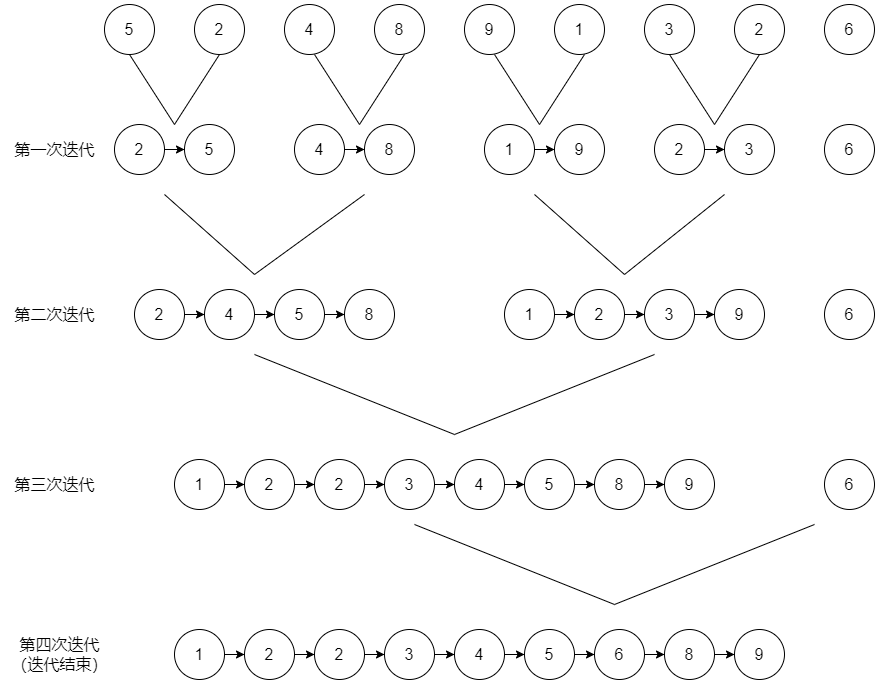
单链表归并排序示意图

流程分析

一次迭代：
1.合并出若干个组 -> 迭代每个组
2.每个组有两个组内部分，内部是有序的
3.合并之后的每个新组，都将作为下一次迭代的组内部分

代码实现

关键代码

class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null) {
            return head;
        }
        int length = 0;
        ListNode node = head;
        while (node != null) {
            length++;
            node = node.next;
        }
        ListNode dummyHead = new ListNode(0, head);
        for (int subLength = 1; subLength < length; subLength <<= 1) {
            ListNode prev = dummyHead, curr = dummyHead.next;
            while (curr != null) {
                ListNode head1 = curr;
                for (int i = 1; i < subLength && curr.next != null; i++) {
                    curr = curr.next;
                }
                ListNode head2 = curr.next;
                curr.next = null;
                curr = head2;
                for (int i = 1; i < subLength && curr != null && curr.next != null; i++) {
                    curr = curr.next;
                }
                ListNode next = null;
                if (curr != null) {
                    next = curr.next;
                    curr.next = null;
                }
                ListNode merged = merge(head1, head2);
                prev.next = merged;
                while (prev.next != null) {
                    prev = prev.next;
                }
                curr = next;
            }
        }
        return dummyHead.next;
    }

    static public ListNode merge(ListNode head1, ListNode head2){
	    ListNode dummy = new ListNode(), p = dummy;
	    ListNode p1 = head1, p2 = head2;
	    while(p1 != null && p2 != null){
		    if(p1.val < p2.val){
			    p.next = p1;
			    p1 = p1.next; // while迭代的最后一步，p = p.next
		    } else {
		    	p.next = p2;
		    	p2 = p2.next; // ---
		    }
		    p = p.next; // while迭代的最后一步，p = p.next
	    }
	    if(p1 != null){
	    	p.next = p1;
	    } else p.next = p2;
	    return dummy.next;
    }
}

快速排序（\(O(NlogN)\)）

超时，因为倒序转升序导致快速排序退化为（\(O(N^2)\)）
快速排序的本质就是：对整体的局部排序，再左右拼接成整体

分隔链表（大区间、小区间）
- 开始分隔时 / 状态起点：
  - 节点：对哪个节点分大小区间
- 迭代 / 单次状态转移过程：
  - 是否需要新链表？
  - 插入原链表，还是大小区间两个链表
  - 是否需要 dummy、如何穿针引线
- 迭代终止条件：
- 分隔结束时 / 状态转移结果：
  - 区间怎么用：递归
递归快排：
- 递什么操作：左右区间分别去排序
- 归什么结果：已排序的左右区间的头节点

代码实现：

class Solution {
    public ListNode sortList(ListNode head) {
		// 传入的链表 为空 或 单节点
        if(head == null || head.next == null){
            return head;
        }
        ListNode p = head.next;
        int x = head.val;
        ListNode left = new ListNode(), pl = left;
        ListNode right = new ListNode(), pr = right;
		// 分隔成左右区间
        while(p != null){
            if(p.val > x){
                pr.next = p;
                pr = pr.next;
            } else {
                pl.next = p;
                pl = pl.next;
            }
            p = p.next;
        }
        pl.next = null; // 很关键，否则成环
        pr.next = null; // 很关键
		
		// 递：左右区间 分别去排序
		// 归：已排序的左右区间 的 头节点
        ListNode sortedLeft = sortList(left.next);
        ListNode sortedRight = sortList(right.next);
		// 将 左区间 和 中间值节点 和 右区间 串联
        pl = sortedLeft;
        if(sortedLeft != null){
            while(pl.next != null){
                pl = pl.next;
            }
            pl.next = head;
        } else sortedLeft = head;
        head.next = sortedRight;
		// 返回排序链表（已排序 的 整体局部）
        return sortedLeft;
    }
}

计数排序（\(O(N)\)）

运行时间：2ms, 击败 100%

class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null) {
            return null;
        }
        int max = head.val;
        int min = head.val;
        ListNode node = head.next;
        while (node != null) {
            int val = node.val;
            if (val > max) {
                max = val;
            }
            if (val < min) {
                min = val;
            }
            node = node.next;
        }
        int[] count = new int[max - min + 1];

        node = head;
        while (node != null) {
            count[node.val - min]++;
            node = node.next;
        }
        node = head;
        max -= min;
        for (int i = 0; i <= max; i++) {
            int val = min + i;
            while (count[i]-- > 0) {
                node.val = val;
                node = node.next;
            }
        }
        return head;
    }
}

posted @ 2023-08-04 20:20 你好，一多阅读(29) 评论(0) 编辑收藏举报

刷新页面返回顶部

就在江湖之上

算法刷题：链表题（8.4，持续更）

解题思维

先核心逻辑，再细节

下标排序和反转链表

链表相交、成环

画图分析

穿针引线图

奇偶节点数链表 - 边界处理

1 多指针迭代

两数相加

未优化的代码（2ms）

优化后代码（1ms击败100%）

合并 2 个有序链表

多指针迭代解法（\(O(N)\))

合并 k 个有序链表

K个中minNode解法 (\(O(K * N)\))

排序队列取minNode队头

手动实现的排序队列解法 (\(O(K * N)\))

优先级队列解法 ( \(O(N log(K))\))

分治解法：两个一组逐渐合并 (\(O(N log(K))\))

分隔链表

多指针迭代解法（\(O(N)\))

2 快慢指针

理论解析：快慢指针的切入点

速度倍数题：

链表的中间节点 ( \(O(N)\) )

删除链表的中间节点 ( \(O(N)\) )

相对速度题：

环形链表 ( \(O(N)\) )

环形链表的环形入口（\(O(N)\)）

数学建模分析

切入点：

首先进入环之前，是有长度的：

环长度还可以分解：

时间线：

公式化简：

分析公式：

代码实现

跟随(pcn) + 穿针引线

反转链表（\(O(N)\)）

快慢指针解法-画图分析、代码实现

递归解法（\(O(N)\)）

新建链表解法(其实类似跟随指针)

反转链表的中间某段 / 反转链表 II

快慢指针解法（\(O(N)\)）

优化代码

K 个一组反转链表

求长度分别反转解法（\(O(K * N)\)）

重排链表

回文链表

思路：链表中间节点+反转链表（相交链表）

反转后半部分解法（\(O(N)\)）

反转前半部分解法（\(O(N)\)，更优）

长短链迭代完成速度题

相交链表

对齐长度解法

求长度·对齐解法（\(O(N)\)）

迭代完成快慢对齐解法（\(O(N)\)）

拼接成环型链表解法（\(O(N)\)）

3 排序

基础排序（\(O(N^2)\)，超时）

冒泡排序

选择排序

插入排序

归并排序（\(O(NlogN)\)）

自顶向下归并

优化代码：

自底向上归并

画图分析和流程分析

代码实现

快速排序（\(O(NlogN)\)）

计数排序（\(O(N)\)）

公告

^{多指针迭代}解法（\(O(N)\))

^{K个中minNode}解法 (\(O(K * N)\))

^{手动实现的排序队列}解法 (\(O(K * N)\))

^{优先级队列}解法 ( \(O(N log(K))\))

^分治解法：两个一组逐渐合并 (\(O(N log(K))\))

^{多指针迭代}解法（\(O(N)\))

^数学建模分析

^快慢指针解法-画图分析、代码实现

^递归解法（\(O(N)\)）

^新建链表解法(其实类似跟随指针)

^快慢指针解法（\(O(N)\)）

^{求长度分别反转}解法（\(O(K * N)\)）

^{反转后半部分}解法（\(O(N)\)）

^{反转前半部分}解法（\(O(N)\)，更优）

^{求长度·对齐}解法（\(O(N)\)）

^{迭代完成快慢对齐}解法（\(O(N)\)）

^{拼接成环型链表}解法（\(O(N)\)）