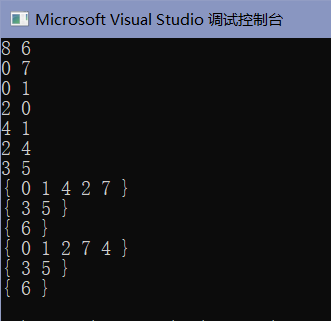
列出连通集的邻接表解题
也许有许多人像我一样,一开始用邻接表做这题,结果发现深搜的顺序是错的导致这题出不来。很多人于是放弃了邻接表,利用邻接矩阵,显然方便很多。但我不信这个邪,咱就一起死磕这题!
先来看看为什么会错。其实你发现深搜是没有问题的,本来深搜就不是唯一的,所以我们的深搜和答案仅仅是顺序不一样而已。
那么答案的顺序是怎样的呢?题目中有“假设我们总是从编号最小的顶点出发,按编号递增的顺序访问邻接点”,显然是按序号从大到小访问顶点。
由于我们是临界表,各个顶点的连接关系可以看作是单链表来实现的,这就要求我们每个顶点后的单链表是递增排序。然鹅我们建立单链表的时候是读到两个顶点,利用前插法在这两个顶点后分别接上另一个顶点。显然输入不是按照递增顺序,这就导致我们为每个顶点建立的单链表不是递增,从而不能满足“按编号递增的顺序访问邻接点”。
好啦,明白问题后,我们想想解决方法。
既然是要死磕邻接表,那么这个存储结构就不变了。想要邻接表做到“按编号递增的顺序访问邻接点”,想来也不难,就是让每个顶点后的单链表按递增顺序排列。
最后一步,让单链表递增排列,那么就只有两种方法了:
1. 待单链表建立完后,对整个单链表进行排序
2. 在生成单链表的时候,按递增顺序确定插入结点位置后再插入
两种方法都行的,只是多写一个接口的问题。为了避免建立完链表后再对它进行一次循环,我选择了第二种方法。
代码
这是一开始的代码。我们只需注意深搜的接口即可,其余的作为解这题的参考。

1 #include <iostream> 2 #include <queue> 3 4 using namespace std; 5 6 //采用邻接表,一下为定义 7 typedef struct ArcNode { 8 int adjvex; 9 struct ArcNode *nextarc; 10 }ArcNode; 11 typedef struct VexNode { 12 int data; 13 struct ArcNode *firstarc; 14 }VexNode,AdjList[10]; 15 typedef struct { 16 AdjList vertices; 17 int vexnum, arcnum; 18 }ALGraph; 19 20 //函数声明 21 void Create(ALGraph &G); 22 void DFS(ALGraph G, int v); 23 void BFS(ALGraph G, int v); 24 25 bool visited_DFS[10] = { false }; 26 bool visited_BFS[10] = { false }; 27 28 int main() { 29 ALGraph graph; 30 Create(graph); 31 //输出深搜 32 for (int i = 0; i < graph.vexnum; i++) { 33 if (visited_DFS[i] == false) { 34 cout << "{ "; 35 DFS(graph, i); 36 cout << "}" << endl; 37 } 38 } 39 //输出广搜 40 for (int i = 0; i < graph.vexnum; i++) { 41 if (visited_BFS[i] == false) { 42 cout << "{ "; 43 BFS(graph, i); 44 cout << "}" << endl; 45 } 46 } 47 return 0; 48 } 49 50 //创建邻接表 51 void Create(ALGraph &G) { 52 int v1, v2; 53 ArcNode *p1, *p2; 54 cin >> G.vexnum >> G.arcnum; 55 for (int i = 0; i < G.vexnum; i++) { 56 G.vertices[i].data = i; 57 G.vertices[i].firstarc = NULL; //初始化为空,避免野指针 58 } 59 //两点确定一边,前插法 60 for (int i = 0; i < G.arcnum; i++) { 61 p1 = new ArcNode; 62 p2 = new ArcNode; 63 cin >> v1 >> v2; 64 p1->adjvex = v2; 65 p2->adjvex = v1; 66 p1->nextarc = G.vertices[v1].firstarc; 67 G.vertices[v1].firstarc = p1; 68 p2->nextarc = G.vertices[v2].firstarc; 69 G.vertices[v2].firstarc = p2; 70 } 71 //cout << "创建" << endl; 72 } 73 74 //深搜 75 void DFS(ALGraph G, int v) { 76 ArcNode *p = new ArcNode; 77 int w = 0; 78 cout << G.vertices[v].data << " "; 79 visited_DFS[v] = true; 80 p = G.vertices[v].firstarc; 81 while (p != NULL) { 82 w = p->adjvex; 83 if (visited_DFS[w] == false) { 84 DFS(G, w); 85 } 86 p = p->nextarc; 87 } 88 } 89 90 //广搜,引入队列作为辅助 91 void BFS(ALGraph G, int v) { 92 queue<int> q; 93 ArcNode *p = new ArcNode; 94 int w = 0; 95 cout << G.vertices[v].data << " "; 96 visited_BFS[v] = true; 97 q.push(v); 98 while (!q.empty()) { 99 v = q.front(); 100 q.pop(); 101 p = G.vertices[v].firstarc; 102 while (p!=NULL) { 103 w = p->adjvex; 104 if (visited_BFS[w] == false) { 105 cout << G.vertices[w].data << " "; 106 visited_BFS[w] = true; 107 q.push(w); 108 } 109 p = p->nextarc; 110 } 111 } 112 }
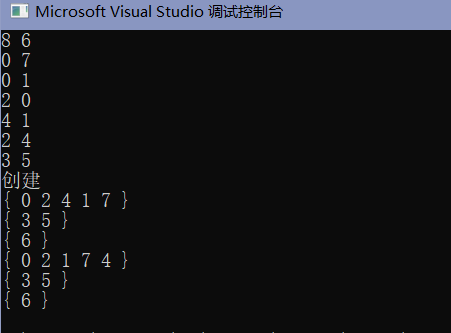
既然决定了要在插入的时候保持链表的升序,就写出以下接口

1 ArcNode* Insert(ArcNode *firstarc, ArcNode *p) { 2 ArcNode *p1, *p2 = NULL; 3 if (firstarc == NULL) { //原链表为空 4 firstarc = p; 5 p->nextarc = NULL; 6 return firstarc; 7 } 8 p1 = firstarc; 9 //定位到要插入的位置 10 while ((p->adjvex > p1->adjvex) && p1->nextarc != NULL) { 11 p2 = p1; //p2记住p1 12 p1 = p1->nextarc; //p1指向后一个结点 13 } 14 if (p->adjvex < p1->adjvex) { //插在p1前 15 p->nextarc = p1; 16 if (firstarc == p1) { //插在表头 17 firstarc = p; 18 } 19 else { //插在表中 20 p2->nextarc = p; 21 } 22 } 23 else { //插在表尾 24 p1->nextarc = p; 25 p->nextarc = NULL; 26 } 27 return firstarc; 28 }
最后,在建立链表的部分进行调整,注意这个部分前后的区别

1 //创建邻接表 2 void Create(ALGraph &G) { 3 int v1, v2; 4 ArcNode *p1, *p2; 5 cin >> G.vexnum >> G.arcnum; 6 for (int i = 0; i < G.vexnum; i++) { 7 G.vertices[i].data = i; 8 G.vertices[i].firstarc = NULL; //初始化为空,避免野指针 9 } 10 //两点确定一边,前插法 11 for (int i = 0; i < G.arcnum; i++) { 12 p1 = new ArcNode; 13 p2 = new ArcNode; 14 cin >> v1 >> v2; 15 p1->adjvex = v2; 16 p2->adjvex = v1; 17 p1->nextarc = G.vertices[v1].firstarc; 18 G.vertices[v1].firstarc = Insert(G.vertices[v1].firstarc, p1); //原为G.vertices[v1].firstarc = p1; 19 p2->nextarc = G.vertices[v2].firstarc; 20 G.vertices[v2].firstarc = Insert(G.vertices[v2].firstarc, p2); //原为G.vertices[v2].firstarc = p2; 21 } 22 //cout << "创建" << endl; 23 }