图的邻接矩阵和邻接表及深度优先搜索
图的邻接矩阵和邻接表
许多人到这一块会比较混乱,特别是邻接表,定义的东西很多,同时也为自己做一个总结。
打算以图的深度优先搜索为例,分别表示邻接矩阵和邻接表。
开始前,为了方便大家对命名的记忆,列出了以下常用单词:
- vertex/vertices:顶点
- arc:弧
- matrix:矩阵
- adjacency matrix:邻接矩阵
- graph:图
- depth-first search:深度优先搜索
邻接矩阵
输出固定为:
5 6 //顶点数,边数
A B C D E //五个顶点的名字
A C 12 //顶点A到顶点E的权值
A E 8
B C 6
C D 5
D E 8
E B 6
先上定义
//邻接矩阵存储
typedef struct {
char vex[10]; //顶点表
int arcs[10][10]; //邻接矩阵
int vexnum, arcnum; //图的信息,顶点总数和边总数
};
邻接矩阵较为简单,将一个二维数组和其他信息打包即可
因为输入数据的时候不一定按顺序来,所以需要一个顶点表记录顶点编号。
C 
/*
输入格式:
5 6 //顶点数,边数
A B C D E //五个顶点的名字
A C 12 //顶点A到顶点E的权值
A E 8
B C 6
C D 5
D E 8
E B 6
*/
#include <iostream>
using namespace std;
//邻接矩阵存储
typedef struct {
char vex[10]; //顶点表
int arcs[10][10]; //邻接矩阵
int vexnum, arcnum; //图的信息,顶点总数和边总数
}AMGraph;
//函数声明
void Create(AMGraph &G);
int Locate(AMGraph G, char v);
void DFS(AMGraph G, int v);
bool visited[10] = { false };
int main() {
AMGraph graph;
Create(graph);
DFS(graph, 0);
//输出邻接矩阵
//cout << endl;
//for (int i = 0; i < graph.vexnum; i++) {
// for (int j = 0; j < graph.vexnum; j++) {
// cout << graph.arcs[i][j] << " ";
// }
// cout << endl;
//}
return 0;
}
//创建无向图
void Create(AMGraph &G) {
char v1, v2; //接收输入的顶点
int x = 0, y = 0, w = 0; //输入的边的权w,对应行标x,列表y
cin >> G.vexnum >> G.arcnum; //总顶点、边数
for (int i = 0; i < G.vexnum; i++) { //依次输入节点信息
cin >> G.vex[i];
}
//初始化邻接矩阵,边均为0
for (int i = 0; i < G.vexnum; i++) {
for (int j = 0; j < G.vexnum; j++) {
G.arcs[i][j] = 0;
}
}
//根据输入的图的边构造矩阵
for (int i = 0; i < G.arcnum; i++) {
cin >> v1 >> v2 >> w;
x = Locate(G, v1);
y = Locate(G, v2);
G.arcs[x][y] = w;
G.arcs[y][x] = w;
}
cout << "创建成功" << endl;
}
//根据顶点名获得其编号下标
int Locate(AMGraph G, char v) {
int result = -1;
for (int i = 0; i < G.vexnum; i++) {
if (G.vex[i] == v) {
result = i;
break;
}
}
return result;
}
//从编号为v的节点开始深度优先搜索并输出节点名
void DFS(AMGraph G, int v) {
cout << G.vex[v] << endl;
visited[v] = true;
for (int i = 0; i < G.vexnum; i++) {
if ((G.arcs[v][i] != 0) && (visited[i] == false)) {
DFS(G, i);
}
}
}
邻接表
输出固定为:
5 6 //顶点数,边数
A B C D E //五个顶点的名字
A C
A E
B C
C D
D E
E B
这里的三个定义比较复杂,相互嵌套绕的有点晕...
//定义边
typedef struct ArcNode{
int adjvex; //边另一头的节点
struct ArcNode *nextarc; //边
}ArcNode;
//定义顶点
typedef struct VexNode {
char data; //顶点信息
ArcNode *firstarc; //边
}VexNode, AdjList[10];
//定义邻接表
typedef struct {
AdjList vertices; //表本体
int vexnum, arcnum; //额外信息,顶点、边总数
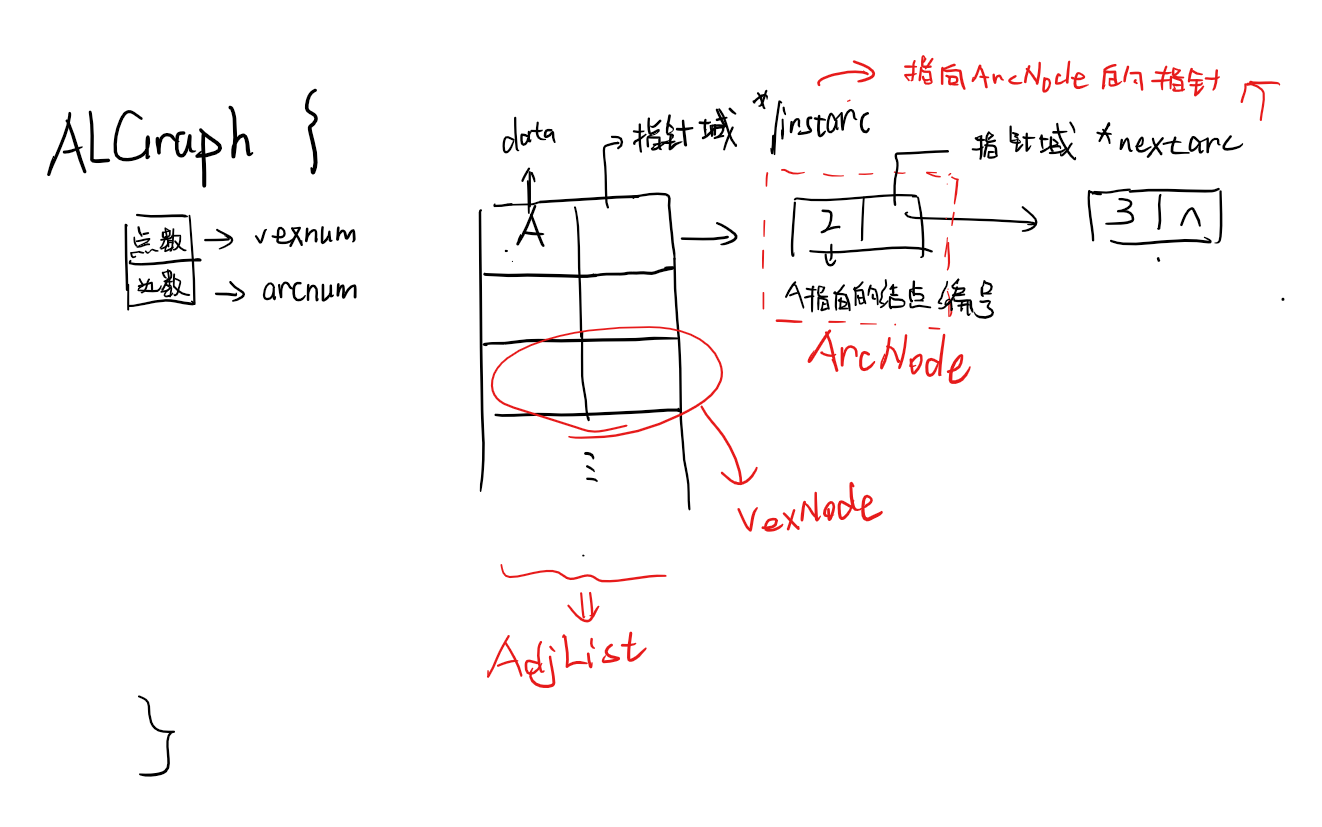
}ALGraph;
三个定义的关系如下
/*
输入格式:
5 6 //顶点数,边数
A B C D E //五个顶点的名字
A C
A E
B C
C D
D E
E B
*/
#include <iostream>
using namespace std;
//定义边
typedef struct ArcNode{
int adjvex; //边另一头的节点
struct ArcNode *nextarc; //边
}ArcNode;
//定义顶点
typedef struct VexNode {
char data; //顶点信息
struct ArcNode *firstarc; //边
}VexNode, AdjList[10];
//定义邻接表
typedef struct {
AdjList vertices; //表本体
int vexnum, arcnum; //额外信息,顶点、边总数
}ALGraph;
//函数声明
void Create(ALGraph &G);
int Locate(ALGraph G, char v);
void DFS(ALGraph G, int v);
bool visited[10] = { false }; //已经被搜索到的顶点变为true,避免重复搜索
int main() {
ALGraph graph;
Create(graph);
DFS(graph, 0);
return 0;
}
//创建
void Create(ALGraph &G) {
char v1, v2; //存输入的两个边
int x = 0, y = 0; //存输入的两个边的编号下标
ArcNode *p1, *p2;
cin >> G.vexnum >> G.arcnum;
for (int i = 0; i < G.vexnum; i++) {
cin >> G.vertices[i].data;
G.vertices[i].firstarc = NULL; //初始化为空,避免野指针
}
//读入两点构建边
for (int i = 0; i < G.arcnum; i++) {
p1 = new ArcNode;
p1->nextarc = NULL;
p2 = new ArcNode;
p2->nextarc = NULL;
cin >> v1 >> v2;
x = Locate(G, v1);
y = Locate(G, v2);
p1->adjvex = y;
p2->adjvex = x;
p1->nextarc = G.vertices[x].firstarc;
G.vertices[x].firstarc = p1;
p2->nextarc = G.vertices[y].firstarc;
G.vertices[y].firstarc = p2;
}
cout << "创建完成" << endl;
}
//根据顶点名得到其对应的编号下标
int Locate(ALGraph G, char v) {
int result = -1;
for (int i = 0; i < G.vexnum; i++) {
if (G.vertices[i].data == v) {
result = i;
break;
}
}
return result;
}
//从编号为v的顶点开始深度优先搜索并输出顶点名
void DFS(ALGraph G, int v) {
ArcNode *p = new ArcNode; //编号为v的顶点的指针
int w = 0; //后一个指针的编号
cout << G.vertices[v].data << endl;
visited[v] = true;
p = G.vertices[v].firstarc;
while (p != NULL) {
w = p->adjvex;
if (visited[w] == false) {
DFS(G, w);
}
p = p->nextarc;
}
}

