Educational Codeforces Round 171 (Rated for Div. 2) 10.28 ABCD题解

Educational Codeforces Round 171 (Rated for Div. 2) 10.28 （ABCD）题解

A. Perpendicular Segments

数学（math）计算几何（geometry）

题意：

给定一个$X,Y,K$。需要求解出二维坐标系中的四个点$A,B,C,D$，满足：$0\le A_x，B_x，C_x，D_x\le X$，$0\le A_y，B_y，C_y，D_y\le Y$。并且$|AB|,|CD|\ge K$。
如果有多个输出，输出任意一个即可。

输入：

第一行一个整数$t$，表示$t$组测试用例。$(1\le t\le 5000)$
每组一行三个整数$X,Y,K$。$(1\le X，Y\le 1000；1\le K\le 1414)$
输入附加限制：输入的$X,Y,K$保证存在答案。

输出：

每组数据两行，第一行四个整数表示$A_x,A_y,B_x,B_y$，中间用空格隔开。
第二行四个整数表示$C_x,C_y,D_x,D_y$，中间用空格隔开。

样例输入：

4
1 1 1
3 4 1
4 3 3
3 4 4

样例输出：

0 0 1 0
0 0 0 1
2 4 2 2
0 1 1 1
0 0 1 3
1 2 4 1
0 1 3 4
0 3 3 0

样例解释：

在第一个样例中，四个点可以如下：

在第二个样例中，四个点可以如下：

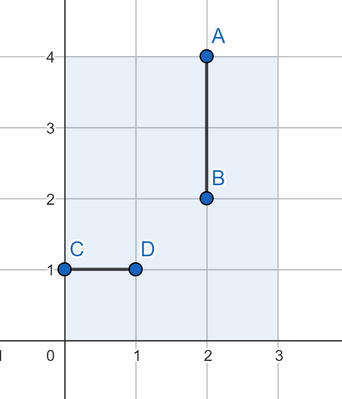
在第三个样例中，四个点可以如下：

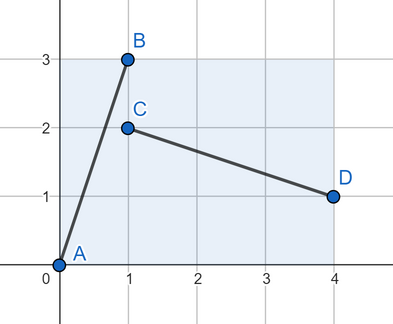
在第四个样例中，四个点可以如下：

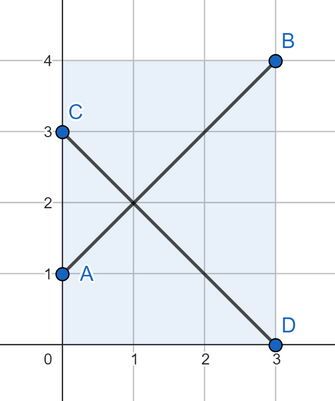
分析：

由于题目给定的输出限制是保证一定有解，那么我们逆向思维，考虑什么限制条件他是无解的。
对于一个矩阵，如果他是正方形对角线一定垂直。这是合理的，那如果是长方形呢？
假设输入的$K>\sqrt{2}\ast min(X,Y)$，也就是他比在矩阵中最大正方形的对角线还要大。也就是这种情况$(X>Y)$：

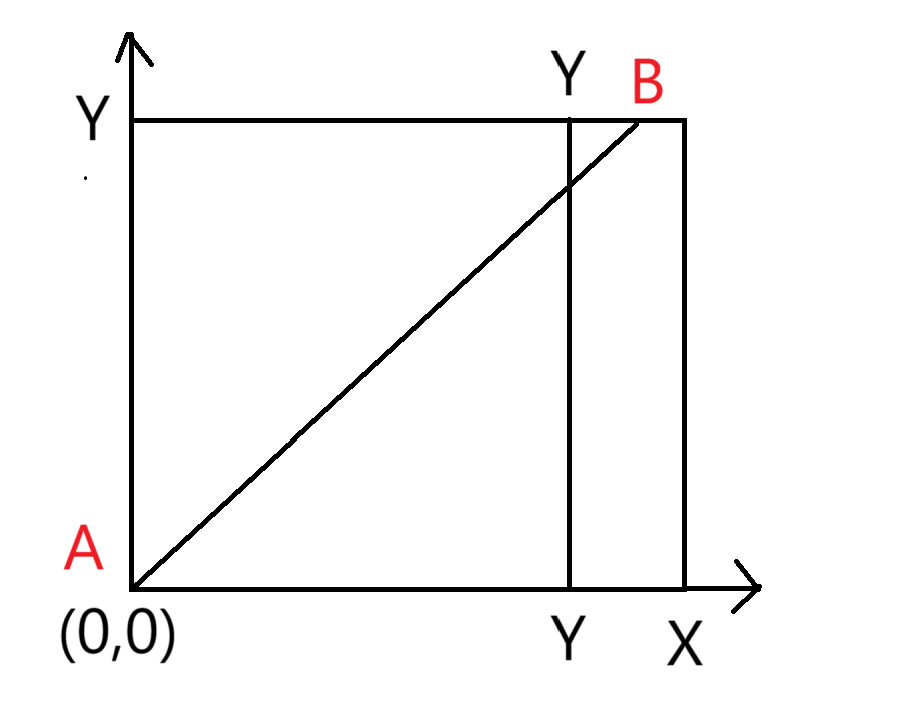
那么我们考虑与$AB$垂直的最长的线段$CD$，判断其是否符合解的情况。

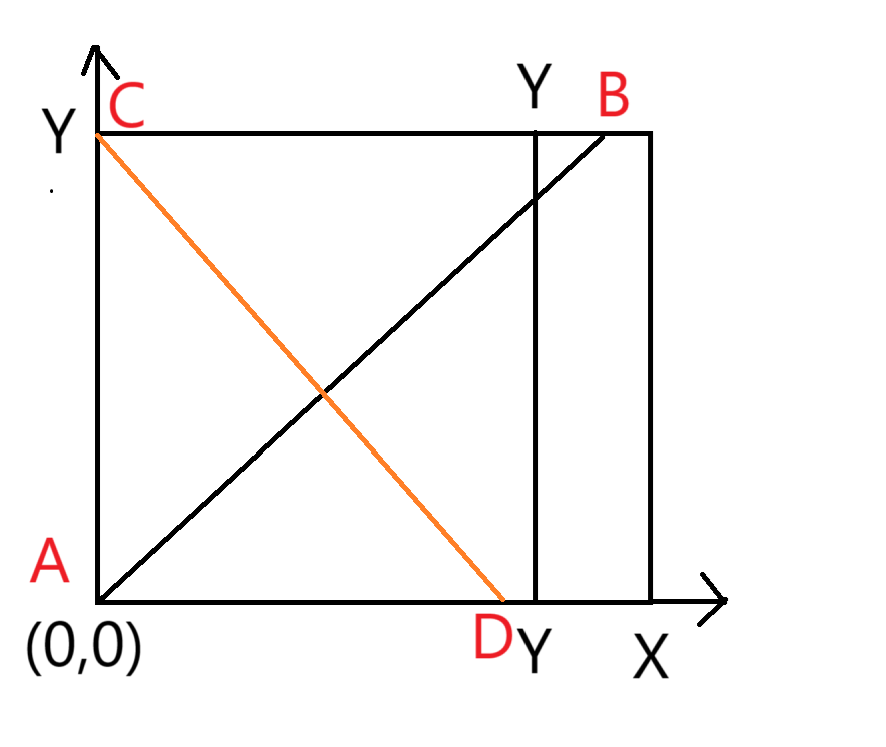
我们证明，可以得到$A$的坐标为$(0,0)$,$B$的坐标为$(t,Y)$，其中$t=\sqrt{K^2-Y^2}$并且有$t>Y$。
我们可以得到$AB$的直线方程为$y=\frac{Y}{t}\ast x$。由于$AB$与$CD$垂直，那么我们可以得到$CD$的直线方程为$y=-\frac{t}{Y}\ast x+Y$。
我们发现，欲求解出最长的$CD$，可以定下来，一定有个点在$(0,Y)$，平移可以证明，这里不证明了。
带入$C$为$(0,Y)$。我们可以解出$D$为$(\frac{Y^2}{t},0)$，接下来我们可以求解出：
$|CD|=Y\ast \sqrt{\frac{Y^2}{t^2}+1}$
$|AB|=\sqrt{Y^2+t^2}=t\ast \sqrt{\frac{Y^2}{t^2}+1}==K$
由于$t>Y$，所以，$|CD|<K$。我们得到长度最大的$|CD|$都无法满足条件，也就是说，输入的一个隐含前提是：$K\le \sqrt{2}\ast min(X,Y)$。
那么我们可以有贪心得到：每次都取最大正方形的对角线作为$|AB|$和$|CD|$。
所以我们输出
$A_x=0,A_y=0$
$B_x=min(X,Y),B_y=min(X,Y)$
$C_x=0,C_y=min(X,Y)$
$D_x=min(X,Y),D_y=0$ 即可。

ac 代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e5+10;
int a[N];
int t,n;
int x,y,k;
signed main() {
    cin>>t;
    while(t--){
        cin>>x>>y>>k;
        int A_x,A_y,B_x,B_y,C_x,C_y,D_x,D_y;
        int m=min(x,y);
        A_x=0,A_y=0;
        B_x=m,B_y=m;
        C_x=0,C_y=m;
        D_x=m,D_y=0;
        cout<<A_x<<" "<<A_y<<" "<<B_x<<" "<<B_y<<endl;
        cout<<C_x<<" "<<C_y<<" "<<D_x<<" "<<D_y<<endl;
    }
    return 0;
}

---

B. Black Cells

二分（binary search） 暴力枚举（brute force）

题意：

有一个长方形格子，从左到右编号为$0$到${10}^{18}$。
给定长度为$n$的数组$a$，起初每个元素对应的格子都是白色的。
每次可以选取数组中的两个元素，$a_i$和$a_j$，如果$i\ne j$并且，$|i-j|\le k$，就可以将这两个格子涂成黑色。
数组$a$中的元素必须要全部涂成黑色，此外，最多有一个不在$a$中的元素可以被涂成黑色。
我们需要求解出符合题意$k$的最小值。

输入：

第一行一个整数$t$，表示$t$组测试用例。$(1\le t\le 500)$
每组第一行一个整数$t$。$(1\le n\le 2000)$
接下来一行$t$个整数$a_1,a_2,\dots ,a_n$。($0<a_i<{10}^{18}$; $a_i<a_{i+1}$)

输出：

每组一行一个整数$k$，表示符合题意答案的最小值。

样例输入：

4
2
1 2
1
7
3
2 4 9
5
1 5 8 10 13

样例输出：

1
1
2
3

样例解释：

在第一个样例中，使用$k=1$可以绘制单元格 $(1,2)$。
在第二个样例中，使用$k=1$可以绘制单元格$(7,8)$。
在第三个样例中，使用$k=2$可以绘制单元格$(2,4)$和$(8,9)$。
在第四个样例中，使用$k=3$可以绘制单元格$(0,1)$、$(5,8)$和$(10,13)$。

分析：

我们发现这个题目，就是需要求出比较合适数对之间最小值，它允许一个元素单独涂。
那么我们很容易发现，当数组长度$n$是偶数的时候，不存在一个元素单独涂的情况，因为每次涂两个，势必还会再单一个元素。
如果$n$是奇数，他就可以单一个元素不考虑。并且这个单独涂的元素也有限制，他只能是奇数位。下标从$1$开始。
因为假设他是偶数位，他前面一定有奇数个元素，再因为两两配对涂色，就一定会导致存在一个单独的元素，前后矛盾了，所以他只能在奇数位单独涂。
基于上面的分析，我们可以采用暴力枚举来完成。
先判断$n$的奇偶，为偶，则直接枚举两个元素，求出差值最大值。
如果是奇数，枚举奇数位单独的情况，再里面枚举两个元素差值的最大值，最后所有这样的单独位得到的结果取最小值。

我们再讲一下另一个思路，由于我们发现结果一定有：$1\le k\le (max(a)-min(a))$。
所以我们考虑二分。枚举这两个端点，二分的条件就是判断这个$mid$是否满足二分条件。

我们来思考一下这个二分$check$应该如何写？
首先我们的大前提是所有$a$中元素涂色，并且，最多只能有一个其他元素进行涂色。
所以我们每次$check$的时候枚举数组，两个元素直接求差值，如果他比$mid$小,就说明这个数对满足条件，再往后枚举。
相反如果不符合，那么直接就将这个元素单独涂色，再往后枚举。
如果上述操作后，有多个元素需要单独处理，就说明我们的$mid$比预期的要小，就更新二分的点。

ac 代码：

//暴力枚举
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2020;
int a[N];
int t,n;
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        for (int i=0;i<n;i++)cin>>a[i];
        int ans=0;
        if(n%2==0) {
            for (int i=0;i<n;i+=2){
                ans=max(ans,a[i+1]-a[i]);
            }
        } 
        else{
            ans=0x3f3f3f3f3f3f3f3f;
            for (int i=0;i<n;i+=2) {
                int res=0;
                for (int j=0;j<n;j+=2) {
                    if (j==i){
                        j--;
                        continue;
                    }
                    res=max(res,a[j+1]-a[j]);
                }
                ans=min(ans,res);
            }
        }
        if(ans)cout<<ans<<endl;
        else cout<<1<<endl;
    }
    return 0;
}

//二分
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2010;
int a[N],b[N];
int t,n;
bool check(int mid){
    int fl=0;
    for(int i=0;i<n;i++){
        if(i+1<n&&a[i+1]-a[i]<=mid)i += 1;
        else fl++;
    }
    return fl<=1;
}
signed main() {
    cin>>t;
    while(t--){
        cin>>n;
        vector<int>B(n);
        for(int i=0;i<n;i++)cin>>a[i];
        int l=1;
        int r=max(l,a[n-1]-a[0]);
        int ans=r;
        while(l<=r){
            int mid=l+r>>1;
            if(check(mid)) {
                ans=mid;
                r=mid-1;
            }
            else l=mid+1;
        }
        cout<<ans<<endl;
    }
    return 0;
}

---

C. Action Figures

贪心（greedy） 数据结构（data structures）

题意：

$Monocarp$要去商店买玩具一共有$n$个玩具即将推出，在第$i$天的时候，商店会推出一个新的玩具，价格为$i$个硬币。
即第$i$个玩具只能在$i$到$n$天购买，但价格不会变化。并且如果$Monocarp$在某一天一次购买多个玩具，那么价格最高的将会免费。
但是$Monocarp$并不会每天都去商店，给一个字符串，其中$0$表示第$i$天不去商店，$1$表示第$i$天去商店。由于第$n$个玩具只能在第$n$天购买，所以他一定是$1$。
需要求解出$Monocarp$买下这些玩具至少需要多少个硬币？

输入：

第一行一个整数$t$，表示$t$组测试用例。$(1\le t\le {10}^4)$
每组第一行一个整数$n$，表示一共有$n$个玩具。($1\le n\le 4\ast {10}^5$)
接下来一行一个长度为$n$的字符串$s$，其中每位为$1$或者$0$，表示去商店或者不去商店。
输入限制，保证$s$末尾一定是$1$。

样例输入：

4
1
1
6
101101
7
1110001
5
11111

样例输出：

1
8
18
6

样例解释：

在第一个样例中，$Monocarp$可以在第$1$天购买第$1$个玩具，花费$1$个硬币。
在第一个样例中，$Monocarp$可以在第$3$天购买第$1$个和第$3$个玩具，花费$1$个硬币，
然后可以在第$4$天购买第$2$个和第$4$个玩具，花费$2$个硬币。
最后可以在第$6$天购买第$5$个和第$6$个玩具，花费$5$个硬币，所以答案是$1+2+5=8$。

在第一个样例中，$Monocarp$可以在第$3$天购买第$2$个和第$3$个玩具，花费$2$个硬币。
之后他在第$7$天买剩下所有的玩具，花费$1+4+5+6=16$个硬币，总共花费$16+2=18$个硬币。

分析：

我们发现，如果存在对应$0$，那么这个玩具一定会被原价购买。
如何证明？

假设第$i$天字符串中对应的为$0$,即$Monocarp$不去商店购买东西，则第$i$个玩具只能放在后面的时间购买。
又因为后面的价格高于$i$，那么后面贵的元素优先考虑打折，所以，不论如何操作，$0$对应的玩具一定会被购买。
那么也就是$1$对应的是可能购买，我们不妨给他存起来。

然后我们再细化考虑其中细节。
我们已经分析了$0$对应的玩具一定会被购买，那么我们还需要最优考虑，
如果$0$后面还存在比他价格高，且是$1$对应的，那么这个玩具就应该是免费的。
由于这个玩具就不需要购买了， 就可以移除掉。
我们可以用队列来实现上述操作。
最后实现完之后考虑队列中元素，我们由于可以免费，所以我们只需要对半向上取整再考虑后半部分较小的元素即可。

ac 代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
void solve()
{
    int n;
    string s;
    cin>>n;
    cin>>s;
    s=' '+s;
    int ans=0;
    int fg=0;
    queue<int> q;
    for(int i=s.size()-1;i>=1;i--)
    {
        if(s[i]=='0')
        {
            if(q.size()) q.pop();
            ans+=i;
        }
        else
        {
            q.push(i);
        }
    }
    int sz=(q.size()/2);
    int tot=0;
    int bk=0;
    while(q.size())
    {
        tot+=q.front();

        if(sz)
        {
            sz--;
            bk+=q.front();
        }
        q.pop();
    }
    tot-=bk;
    cout<<ans+tot<<endl;

}
signed main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int tt=1;
    cin >> tt;
    while(tt--) solve();
}

---

D. Sums of Segments

数学（math）二分（binary search）

题意：

给定一个长度为$n$的数组$[a_1,a_2,\dots ,a_n]$。
设定$s(l,r)$是从$a_l$ 到$a_r$的元素之和，即： $s(l,r)=\sum _{i=l}^r{a}_i$。
再构造一个长度为$\frac{n(n+1)}{2}$的数组$b$。 $b=[s(1,1),s(1,2),\dots ,s(1,n),s(2,2),s(2,3),\dots ,s(2,n),s(3,3),\dots ,s(n,n)]$。
例如：$a=[1,2,5,10]$，那么$b=[1,3,8,18,2,7,17,5,15,10]$。
之后会有$q$次查询，每次给定$l,r$需要求解出$\sum _{j=l_i}^{r_i}{b}_j$，即数组$b$中$l$到$r$的元素之和。

输入：

第一行一个整数$n$，表示数组$a$的元素个数。$(1\le n\le 3\ast {10}^5)$
第二行$n$个整数$a_i$。$(-10\le a_i\le 10)$
第三行一个整数$q$，表示$q$次查询。$(1\le q\le 3\ast {10}^5)$
接下来$q$行，每一行两个整数$l_i$和$r_i$。$(1\le l_i\le r_i\le \frac{n(n+1)}{2})$

样例输入：

4
1 2 5 10
15
1 1
1 2
1 3
1 4
1 5
1 10
5 10
6 10
2 8
3 4
3 10
3 8
5 6
5 5
1 8

样例输出：

1
4
12
30
32
86
56
54
60
26
82
57
9
2
61

分析：

我们发现这是一个数组构造的题目。那么我们来找规律。
我们单纯考虑样例。

索引	1	2	3	4
a	1	2	5	10

$b=[1,3,8,18,2,7,17,5,15,10]$可以拆分成4行，第一行是$1,3,8,18$，第二行是$2,7,17$，第三行是$5,15$，第四行是$10$。
那么我们也列出表格

a	1	2	5	10
b	1	3	8	18
		2	7	17
			5	15
				10

我们可以立马发现，在第二行中，每个元素都减去了$a_1$，这个由定义也可以得到，同理第三行第四行均都有这样的操作，并且还多减去$a_2$。第四行多减去了一个$a_3$。
那么我们再更新一下这个表格，补全前面空余的部分。

a	1	2	5	10
b	1	3	8	18
	-4	2	7	17
	-4	-6	5	15
	-4	-6	-10	10

这前面的负数，表示第一行的和加上这几个负值，就可以得到这一行的和。

怎么求？
我们定义的这个负值，是表示这一行减去了多少个$a_i$。
所以$su{b}_i=a_i\ast (n-i+1)$

例如：第一行和是$1+3+8+18=30$，第二行的和是$30+(-4)=26=2+7+17$。
那么这里就可以迅速得到：
前两行的和就是$30\ast 2+(-4)=56$。
前三行的和就是$30\ast 3+(-4)+(-4-6)=76$。
我们发现每一行减去的都是$sub$的一个前缀，所以我们将$sub$取一个前缀和得到：$s_{sub}$。
我们又发现快速求前几行，他每次都是减去的$s_{sub}$的前缀，所以我们再对他取一个前缀和得到：$s_{s_{sub}}$。
对于我们每次对标的第一行，不难发现，他其实是$a$的前缀和的前缀和。我们定义$s_{s_a}$为$a$的前缀和的前缀和。
这样操作，我们取前k行结果就是 $s_{s_a}[n]\ast k-s_{s_{sub}}[k-1]$

对于这个样例，当前的值如下：

a	1	2	5	10
$s_a$	1	3	8	18
$s_{s_a}$	1	4	12	30
$sub$		-4	-6	-10
$s_{sub}$		-4	-10	-20
$s_{sub}$		-4	-14	-34

那么我们取前k行的操作就结束了。
我们再考虑如果他是第二行的第一个元素咋办？
我们只需要取$s_{s_a}[2]$，这样得到4。我们再看需要减去这两个元素多出来的$a_1$但是我们并没有预处理好的两倍的$a_1$。我们仅仅有$su{b}_1$，表示减去了4次。
但是我们可以加呀，我们后面的元素可以快速找出来，有$2$个。我们先给他减去$su{b}_1$,然后再加上$2\ast a_1$就可以得到这一行的结果为$2$。

同理我们也可以搜索第二行第二个数，这样就需要重复减去$a_1$和$a_2$这个我们用$a$前缀和$s_a$可以快速实现。

接下来我们回到问题本身，给出询问，找到$b$数组中，第$l$到第$r$之间的元素和$\sum _{j=l}^r{b}_j$。
那么我们可以看成第$1$个到第$r$个减去第$1$个到第$l-1$个,即$ans=\sum _{j=1}^r{b}_j-\sum _{j=1}^{l-1}{b}_j$

我们根据上面的思路，先搜索他在$l-1$和$r$在第几层。我们可以用二分快速搜，搜到他在第$k$层。

如何搜？
我们通过公式发现，他是一个$n,n-1,n-2,\dots ,1$的一个序列，我们前$k$层的元素有多少个？
$\frac{(n+n-k+1)}{2}$个，用这个条件来二分即可。

我们搜到的结果是向下取整的（如果正好是整的，就不需要后面的操作了），然后再按照上面思路加上第k+1层前面的这些元素就可以了。

ac 代码：

//建议大家按照上面的思路自己写一下，我这个代码可读性很差。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=300010;
int a[N],s[N],ss[N];
int b[N],bb[N];
int t,n,q;

bool check(int k,int x){
    int tmp=(2*n-k+1)*k/2;
    if(tmp>x)return false;
    else return true;
}

signed main() {
    cin>>n;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=n;i++)s[i]=a[i]+s[i-1];
    for(int i=1;i<=n;i++)ss[i]=s[i]+ss[i-1];

    for(int i=1;i<n;i++){
        b[i]=a[i]*(n-i+1);
    }
    for(int i=1;i<n;i++)b[i]+=b[i-1];
    for(int i=1;i<n;i++)bb[i]=b[i]+bb[i-1];

    cin>>q;
    while(q--){
        int l,r;
        cin>>l>>r;
        l-=1;
        int k_l=0,k_r=n;
        int L=0,R=0;
        while(k_l<k_r){
            int mid=k_r+k_l+1>>1;
            if(check(mid,l)){
                k_l=mid;
            }
            else{
                k_r=mid-1;
            }
        }
        
        L+=ss[n]*k_l-bb[k_l-1];
        int tmp=l-(2*n-k_l+1)*k_l/2;
        int k=k_l+tmp;
        if(tmp)L+=ss[k]-b[k_l]+s[k_l]*(n-k);
        
        k_l=0,k_r=n;
        while(k_l<k_r){
            int mid=k_r+k_l+1>>1;
            if(check(mid,r)){
                k_l=mid;
            }
            else{
                k_r=mid-1;
            }
        }
        R+=ss[n]*k_l-bb[k_l-1];
        tmp=r-(2*n-k_l+1)*k_l/2;
        k=k_l+tmp;
        if(tmp)R+=ss[k]-b[k_l]+s[k_l]*(n-k);
        int ans=R-L;
        cout<<ans<<endl;
    }
    return 0;
}