Codeforces Round 982 (Div. 2) 10.26 （ABC）题解

Codeforces Round 982 (Div. 2) 10.26 （ABC）题解

A. Rectangle Arrangement

数学（math）

题意：

有一个无限长宽的方形网格，初始为白色，现在有\(n\)个印章，每个印章有自己的宽\(w_i\)和高\(h_i\)。
印章会使得网格涂色，变成黑色。这\(n\)个印章都需要使用一次，需要求解出最后网格中黑色区域周长的最小值。

输入：

第一行一个整数\(t\)，表示\(t\)组测试用例。\((1 \leq t \leq 500)\)
每组第一行一个整数\(n\),表示\(n\)个印章。\((1 \leq n \leq 100)\)
接下来\(n\)行，每行两个数\(w_i\)和\(h_i\)，表示印章的宽和高。\((1 \leq w_i,h_i \leq 100)\)

输出：

每组一行一个整数数据，表示黑色区域周长的最小值。

样例输入：

5
5
1 5
2 4
3 3
4 2
5 1
3
2 2
1 1
1 2
1
3 2
3
100 100
100 100
100 100
4
1 4
2 3
1 5
3 2

样例输出：

20
8
10
400
16

样例解释：

在第一个样例中，印章使用方法如下：

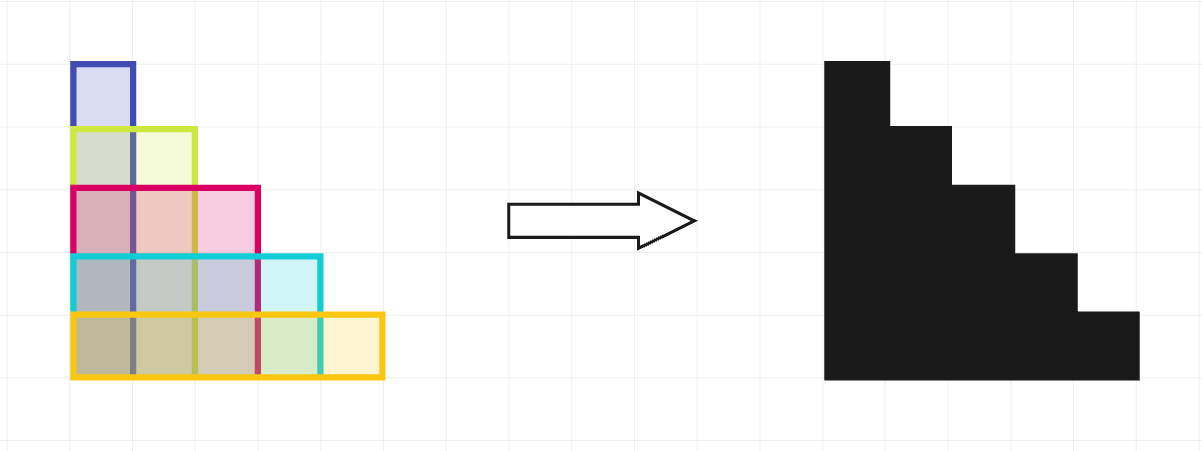
可以看出来周长为\(20\)。
在第二个样例中，第二个印章与第三个印章可以完全在第一个印章的区域中使用，所以结果为\(8\)。

分析：

我们发现，印章可以有重复的堆叠，就像样例一的操作一样，我们可以将他们都堆叠在左下角。
再因为不规则的这种类似于阶梯的图形，周长求解可以平移成一个矩阵。
所以我们很容易可以得到，最小的周长就是他\(2 \ast (左边的长度+底边长度)\)。
在通过观察发现，这两个长度分别就是\(max(w_i)\)和\(max(h_i)\)。
所以答案可以得到：\(2 \ast (max(w_i)+max(h_i))\)。

ac 代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
int t,n;
signed main() {
    cin>>t;
    while(t--){
        cin>>n;
        int max_w=0,max_h=0;
        while(n--){
            int w,h;
            cin>>w>>h;
            max_w=max(max_w,w);
            max_h=max(max_h,h);
        }
        cout<<2*(max_w+max_h)<<endl;
    }
    return 0;
}

B. Stalin Sort

贪心（greedy） 暴力枚举（brute force）

Stalin排序，是一种删去比前面元素小的排序，例如：\([1, 4, 2, 3, 6, 5, 5, 7, 7]\)在Stalin排序之后得到： \([1, 4, 6, 7, 7]\)。
我们定义一个数组为“脆弱数组”，他是在原数组的子数组上采用不限次数的Stalin排序，得到一个非递增的序列。
请问给定任意一个数组，需要删除至少多少个元素，可以使得其为“脆弱数组”。

输入：

第一行一个整数\(t\)，表示\(t\)组测试用例。\((1 \leq t \leq 500)\)
每组第一行一个整数\(n\)，表示原数组大小。\((1 \leq n \leq 2000)\)
接下来一行\(n\)个数字\(a_i\)。\((1 \leq a_i \leq 10^9)\)

输出：

每组输出一个整数，表示最少需要删除的元素个数。

样例输入：

6
7
3 6 4 9 2 5 2
5
5 4 4 2 2
8
2 2 4 4 6 6 10 10
1
1000
9
6 8 9 10 12 9 7 5 4
7
300000000 600000000 400000000 900000000 200000000 400000000 200000000

样例输出：

2
0
6
0
4
2

样例解释：

在第一个测试案例中，最佳答案是删除数字\(3\)和\(9\)这样就只剩下\(a = [6,4,2,5,2]\)
为了证明这个数组是脆弱的，我们可以首先对子数组\([4,2,5]\)进行Stalin排序，得到\(a=[6,4,5,2]\)，然后对子数组\([6,4,5]\)进行Stalin排序，
可以得到 \(a=[6,2]\)，它是不递增的。

在第二个测试案例中，数组已经是非递增的了，所以我们不需要删除任何整数。

分析：

根据题目我们得知：Stalin排序是可以删除掉后面所有比他小的元素。
可以得到，我们对于某一个元素，可以得知他得到脆弱序列的操作应该是删除掉他前面的全部元素和后面比他大的元素即可。
我们会发现，这个解法似乎存在一个漏洞，如果是\(1,4,3,5,1\)这样的序列，对于\(3\)这个元素而言，他应该删除掉\(1,5\)即可，但是我们上面更新的步骤是删除掉\(1,4,5\)。
我们来证明一下为什么放在整体中这样是对的：

如果存在\(i,j\)\((i < j)\)，并且\(a_i>a_j\)，对于这样的序列。
假设\(i\)后面大于\(a_i\)的元素个数为\(s_k\)个，\(i\)后面大于\(a_i\)的元素个数为\(t_k\)个。
由于\(a_i>a_j\)。所以，一定有\(s_k < t_k\)。也就是后续\(i\)删除的元素个数比\(j\)一定会少。
再因为\(i < j\)，所以前面删除的元素，\(i\)比\(j\)一定会少。
所以综上如果\(i,j\)\((i < j)\)，并且\(a_i>a_j\)，在第\(i\)位已经更新到比较小的了，就不需要考虑比\(a_i\)小的元素了。

这个比直接枚举又会更优一些。

ac 代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=2010;
int a[N];
int t,n;
signed main() {
    cin>>t;
    while(t--){
        cin>>n;
        for(int i=0;i<n;i++)cin>>a[i];
        int ans=0x3f3f3f3f3f3f3f3f;
        int count=0;
        for(int i=0;i<n;i++){
            int cnt=0;
            if(a[i]>count){
                count = a[i];
                for(int j=i+1;j<n;j++){
                    if(a[j]>a[i])cnt++;
                }
                ans=min(cnt+i,ans);
            }
            
        }
        cout<<ans<<endl;
    }
    return 0;
}

C. Add Zeros

DFS及其变种（dfs and similar）图论（graphs）

题意：

给定一个长度为\(n\)的数组，现在可以对元素\(a_i\)\((1 \leq i \leq n)\)进行判断，如果\(a_i = |a|+1-i\)\((|a|表示a数组的大小。)\)，就可以在数组后面添加\(i-1\)个\(0\)。
需要求解出，数组操作后预期的最大元素个数。

输入：

第一行一个整数\(t\)，表示\(t\)组测试用例。\((1 \leq t \leq 1000)\)
每组第一行一个整数\(n\)，表示初始的数组大小。\((1 \leq n \leq 3 \ast 10^5)\)
接下来一行\(n\)个整数\(a_i\)。\((1 \leq a_i \leq 10^{12})\)

输出：

每组一个整数，表示操作后预期数组长度的最大值。

样例输入：

4
5
2 4 6 2 5
5
5 4 4 5 1
4
6 8 2 3
1
1

样例输出：

10
11
10
1

样例解释：

在第一个样例中，我们可以先选择第四位元素\(2\)，操作完成后，数组大小为\(5+3=8\)。
然后我们可以选择第三位元素\(6\)，操作完成后数组大小为\(8+2=10\)。

在第二个样例中，我们可以先选择第二位，再选择第三位，最后选择第四位，这样元素个数就变为\(5+1+2+3=11\)。

分析：

我们发现，选定可以操作的数，每次操作后还需要再重新选择，并且同一层有多个元素可以选择的时候，我们无法保证哪一个更优。
鉴于以上分析，我们可以将每一个都遍历一下，类似于DFS深搜的思想，考虑这个点是否更优，选择更优的节点。
由于这个图是一个多到多的图，所以用DFS一定会TLE，再由于对应某一个节点，最多他只能对应某一层，因为他的值是固定的，只有遇到特定的数组长度，他才可以进行操作。
所以我们可以存一下这个点搜索到的最优值，用记忆化搜索来实现这个问题。

接下来我们考虑什么样的元素才会处在同一层操作里面：
我们发现长度为\(k\)的数组中元素\(a_i\)：\((a_i=k-i+1)\)，元素\(a_j\)：\((a_j=k-j+1)\)
他们的共同点是数组元素长度相同，所以我们考虑到这一点，确定\(a_i\)的值为\(a_i+i-1\)，\(a_j\)的值为\(a_j+j-1\)。
值相同的就可以放在同一层操作。
那么如何找到下一层？
我们发现，第\(i\)位的下一次数组长度会更新为\(k+i-1\)，所以我们可以通过这个信息来更新下一次层数组的长度。

综上我们可以通过，DFS+记忆化来通过这个题目。

ac 代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=300010;
int a[N];
int t,n;
int cnt=0;
unordered_map<int,vector<int>>A;
unordered_map<int,int>B;
int fun(int k){
    if(B.count(k))return B[k];
    int res=k;
    for(int i=0;i<A[k].size();i++){
        res=max(res,fun(A[k][i]-1+k));
    }
    B[k]=res;
    return res;
}
signed main() {
    cin>>t;
    while(t--){
        cin>>n;
        A.clear();
        B.clear();
        for(int i=1;i<=n;i++){
            cin>>a[i];
            if(i>1)A[a[i]+i-1].push_back(i);
        }
        cout<<fun(n)<<endl;
    }
    return 0;
}