二叉树的四种遍历方式
- 二叉树的遍历（traversing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问依次且仅被访问一次。
四种遍历方式分别为：先序遍历、中序遍历、后序遍历、层序遍历。
PS：由于在二叉树这一个分类中都能找到对应的代码，所以详细代码就不在这里贴了
一、先序遍历
- 访问根节点
- 用先序遍历的方式访问左子树
- 用先序遍历的方式访问右子树
图的思维过程
- 访问根节点A
- A分为左右两个子树，递归调用，所以遵循“根节点-左-右”，所以访问B节点
- 同2步骤，访问D节点
- 此时D没有分支，回溯到B访问F节点
- 同2步骤，访问E节点，同4步骤，回溯F，F右儿子为空，回溯B，B左右儿子遍历完毕，回溯A，此时A的左子树已经遍历完成，开始遍历右子树
- 同样访问节点C
- 同步骤2访问节点G
- G左子树为空，访问右儿子H
- H没有分支，回溯G，G遍历完成，回溯C，遍历I节点，这样整棵树就已经遍历完成。
遍历结果：A BDFE CGHI
二、中序遍历
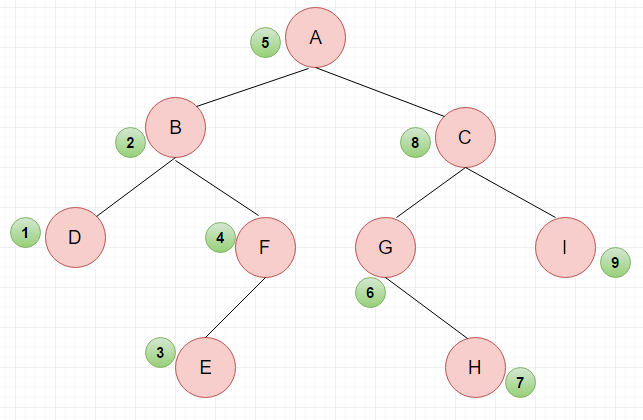
- 用中序遍历访问左子树
- 访问根节点
- 用中序遍历访问右子树
过程跟先序遍历差不多，这里不多叙述。
遍历结果：BDEF A GHCI
三、后序遍历
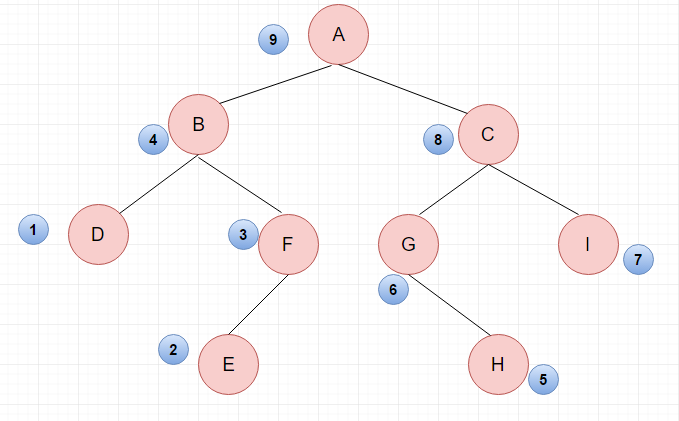
- 用后序遍历访问左子树
- 用后序遍历访问右子树
- 访问根节点
过程跟先序遍历差不多，这里不多叙述。
遍历结果 DEFB HGIC A
小结
三种遍历方法基本路线是一样的，只是访问每个节点的时机不同形成了不同的输出。
四、层序遍历
层序遍历所要解决的问题很好理解，就是按二叉树从上到下，从左到右依次打印每个节点中存储的数据。
层序遍历跟上面三种遍历有些不一样，层序遍历采用的是数据结构中的队列。
- 根节点入队
- 访问队首元素，左儿子若不为空则左子叶入队，右儿子若不为空则入队
- 队首元素出队
- 重复3 、4步骤，直到队列为空为止
图的思维过程
- A入队
- 访问队首A，左儿子不为空，B入队，右儿子不为空，C入队，A出队
- 访问队首B，左右儿子为空，不用操作，B出队
- 访问队首C，同步骤2
- 访问队首D，同步骤3
- 访问队首E，同步骤2
- 访问队首F，同步骤3
- 访问队首G，同步骤3
遍历结果 ABCDEFG
