点分治是否容斥

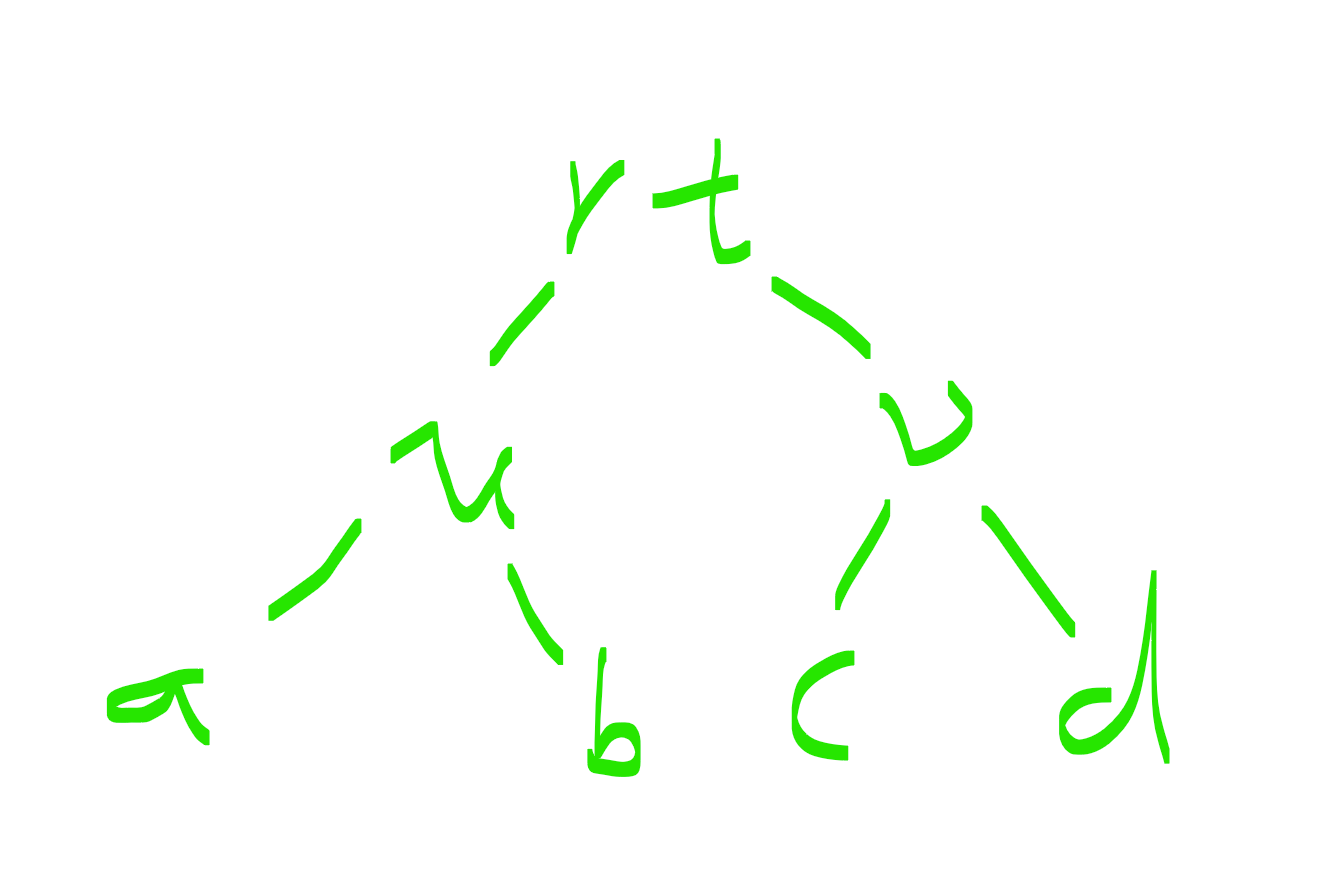
该图涉及的链为

\(rt-u\\rt-u-a\\rt-u-b\\rt-v\\rt-v-c\\rt-v-d\)

还有

\(a-u-rt-u-b\\c-v-rt-v-d\)

发现后面两个是不符合题意的

于是我们要删去这两个

于是我们进来rt-u这里

获得这两个链 于是我们减去这两个链

$rt-u-a\ rt-u-b $

int dep[maxn],a[maxn];
void dfsdeep(int u,int fa){
    a[++a[0]]=dep[u];
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v]||v==fa)continue;
        dep[v]=dep[u]+Len[i];
        dfsdeep(v,u);
    }
}
void cal(int u,int now,int op){
    dep[u]=now,a[0]=0;
    dfsdeep(u,0);
    for(int i=1;i<=a[0];i++){
        for(int j=1;j<=a[0];j++){
            num[a[i]+a[j]]+=op;
        }
    }
}
void solve(int u){
    vis[u]=1;
    cal(u,0,1);
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v])continue;
        cal(v,Len[i],-1);
        sum=sz[v];
        root=0;findroot(v,0);
        solve(root);
    }
}

当然 还有一种不需要容斥的做法，我们发现 唯一的区别就是\(u,v\) 重复了。

于是我们可以通过先进入\(u\)然后再计算u的所有答案。

int a[N], dis[10000003];
int md[N], MK, cnt;
void getdis(int now, int pre, int di) {
	if (di > MK)return ;
	md[++cnt] = di;
	for (auto k : v[now]) {
		if (vis[k.fi] || k.fi == pre)continue;
		getdis(k.fi, now, di + k.se);
	}
}
int qa[N], tmp;
void get(int now, int pre) {
	dis[0] = 1;
	for (auto k : v[now]) {
		if (k.fi == pre || vis[k.fi])continue;
		cnt = 0;
		getdis(k.fi, now, k.se);
		for (int i = 1; i <= cnt; ++i) {
			for (int j = 1; j <= m; j++) {
				if (q[j] >= md[i])a[j] |= dis[q[j] - md[i]];
			}
		}
		for (int i = 1; i <= cnt; i++)dis[md[i]] = 1, qa[++tmp] = md[i];
	}
}
void dfs(int now) {
	vis[now] = 1;
	tmp = 0;
	get(now, 0);
	for (int i = 1; i <= tmp; i++)dis[qa[i]] = 0;
	for (auto k : v[now]) {
		if (vis[k.fi])continue;
		rt = 0;
		n = sz[k.fi];
		root(k.fi, 0);
		dfs(rt);
	}
	return ;
}
————————————————
版权声明：本文为CSDN博主「pubgoso」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_40655981/article/details/100886381